Bonjour,
je cherche à connaitre le poids max que l'on peut mettre sur une lambourde de massaranduba.
65 mm h x 40 mm l
appuie au deux extrémités 16 CM, avec une distance de 3M
l'information semble compliquer à trouver,
je n'ai pas trouvé un logiciel qui peut faire le calcul, pour les résineux pas de problème, par contre les bois exotiques...
5 réponses
Bonjour,
Tu devrais trouver les caractéristiques mécaniques icitropix.cirad.f...hes-disponibles
Et en plus c'est en français !
Tout cela peut s'expliquer avec la théorie de la résitance des matériaux, ou RDM, ce qui est la même chose.
La résistance en flexion s'exprime comme une contrainte (en méga Pascal, ou MPa).
Elle n'a rien à voir avec la flèche (ou déformation), qui elle est proportionnelle au module élastique du matériau considéré et à la charge. Module élastique qui s'exprime en Pascal également. Effectivement, si le module élastique est deux fois plus grand, alors la flèche sera deux fois moindre. Mais cela ne nous renseigne aucunement sur la capacité de ladite poutre à supporter son chargement.
Pour cela, il faut s'intéresser à sa résistance en flexion, que l'on doit comparer à la contrainte dans toute la poutre et voir si la contrainte interne reste inférieure (auquel cas cela ne casse pas) ou atteind/dépasse la résistance en flexion (là ça casse).
La contrainte est proportionnelle à la charge. Une charge deux fois plus grande entraine une contrainte deux fois plus importante. La contrainte est indépendante du module élastique (cf ici), elle dépend uniquement des propriétés de section de poutre considérée, du point de la section considéré et du chargement.
Et donc,
- si tu as la charge maxi admissible sur une poutre en résineux, avec une contrainte admissible en flexion de 24 MPa:
- alors la charge maxi admissible pour une poutre de résistance 12 MPa sera deux fois moindre;
- ou alors la charge maxi admissible pour une poutre de résistance 48MPa sera deux fois supérieure.
- sinon, faut faire une règle de trois
Supposons que tu connaisses la résistance à la flexion d'un matériaux connu, par exemple, un résineux.
Tu peux alors faire des essais comparatifs:
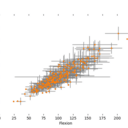
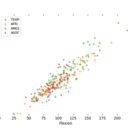
Sur une poutre de même caractéristique (largeur, épaisseur, longueur) que ta poutre en massaranbuba, tu mets un poids au milieu, et tu mesures la flèche.
Tu fais la même chose pour la poutre en massaranduba.
La comparaison des flèches te donnera la limite relative comparée au résineux.
Si la flèche est deux fois moins importante pour le massaranduba, alors, la résistance à la flexion du massaranduba sera deux fois supérieure.
Attention, la limite de flambement (quand cela casse) n'est pas tout à fait la même chose (on peut avoir des matériaux flexibles, mais qui ne flambent pas), mais cela te donnera quand même une bonne idée.





bonjour
pour moi je ne comprend pas votre question car ce n est pas claire du tout on fait un calcul avec un problème et l on explique ce que l' on veut faire et a ce moment la on essaie de trouver une solution
dans les métier du bois du bâtiment il y a un problème de flexion admissible 1, 300 me de la porté et l on indique quelle charge on doit appliqué suivant sa situation
pour le bois il faut le voir pour estimer sa résistance et son sens de débit
le charpentier de service
ou l' homme qui s'est faire un calcul ou du moins une estimation