Suite au pas à pas de trente six seb
Ajustage d'un panneau biais dans un angle.
Principes généraux suivi de la réalisation pratique en atelier.
L'ajustage d'un panneau biais est un problème qui se présente relativement souvent en menuiserie.
trente six seb l'a résolu par approche successives en terme de métier il à perché et cela marche très bien.
Je vais vous présenter deux méthodes pour résoudre le problème par l'épure.
Première solution : Le rabattement du panneau, C'est la méthode classique elle est un peu longue et nécessite des reports assez nombreux.
Deuxième solution : Celle que l'on va utiliser en atelier qui utilise les traces des plans.
Liste des articles
Solution 1 rabattement du panneau
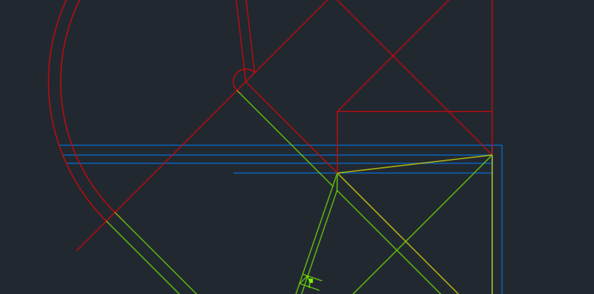
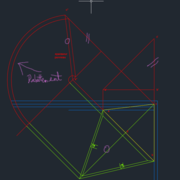
On commence par tracer la vue en plan sur le dessin en jaune a,b,c sont les points du panneau en plan.
Au dessus on trace l'élévation ceci pour la compréhension du dessin car dans le cas présent elle ne sert pas à grand chose sinon à avoir la hauteur du panneau donc a',b',c' sont les points en élévation.
A ce stade il faut considérer l'arête ab comme la trace du plan du panneau (c'est son intersection avec le plan horizontal de référence). Cette arête va nous servir de charnière pour rabattre le panneau sur le plan horizontal et ainsi avoir sa vraie grandeur pour pouvoir le tailler.
Donc pour avoir la vraie grandeur il faut définir la ligne de plus grande pente du panneau, elle est toujours perpendiculaire à la trace en plan ici ab et passe par le sommet c du panneau et fini sur la trace en plan en d(voir dessin)
Perpendiculairement à ab on fait l'élévation de la ligne de plus grande pente dc.
a'' c'' est la vraie grandeur de la ligne de plus grande pente, on porte parallèlement l'épaisseur du panneau. Déjà on la coupe de pied du panneau.
Voilà on à toutes les données pour procéder au rabattement du panneau sur le plan horizontal . ici il est représenter en vert , on fait apparaitre les épaisseurs. Tout est en vraie grandeur je peux donc obtenir les angles de corroyage par coupe rabattues. Pour ceci couper l'arête par deux traits perpendiculaire espacé de l'épaisseur du panneau, puis relier dans la diagonale. On obtient les angles de corroyage ici différent car ici j 'ai tenu compte de l'inclinaison d'un des cotés comme dans le cas de SEB.
Voilà on peut tailler alors on peut considérer que c'est un peu long et cela nécessite une épure un peu conséquente.
Dans un atelier on va plutôt procéder avec une autre méthode, celle ci permet de bien comprendre le processus et d'aller plus loin ensuite.
Solution 2
Ici on va faire appel au trace du plan.
on trace la vue en plan a,b,c , on trace la ligne de plus grande pente d,c.
Par changement de" plan je trace la vraie grandeur de la ligne de plus grande pente d,e ; c,e est la hauteur du panneau porté perpendiculairement à la trace en plan de la ligne de plus grande pente d,c.
en me servant de a, b comme charnière je porte la vraie grandeur de la ligne de plus grande pente d,e en d,e'.
On relie le tout et j'ai la vraie grandeur du panneau a,b,e'. Pour l'angle de corroyage couper l'arête a,e' en f perpendiculairement puis venir couper la trace en plan a,b en g. Rabattre f,g sur la vue en plan en h . L'angle de corroyage est ghc.
Voila il faut un petit quart d'heure il y a moins de report et donc une meilleur précision.
Mais la méthode est plus abstraite que la première solution






Discussions
Merci !!
Je ne l'ai pas lu. Je veux y réfléchir au préalable.
J'ai quand même vu les titres et la méthode de rabattement est la première que je voulais essayer.
Si je suis d’attaque, je fais ça ce week end.
Ah l’arêtier !!!
Pour calculer l'angle dièdre de deux plans, il y a aussi mon petit calculateur
Donc je n'ai toujours pas lu le pas à pas, seulement l'introduction.
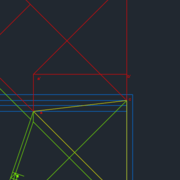
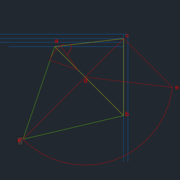
Voici ce que j'ai fait. J'ai simulé 2 panneaux biais. L'un (à gauche) est le plus simple, il ferme le coin d'un cube donc tous les plans de rencontre sont à angle droit les uns des autres. Le deuxième (à droite donc) s'appuie sur un plan biais, les autres restants orthogonaux.
Mon idée est de changer de plan pour voir mon triangle de profil puis de le rabattre sur un plan horizontal. Je pensais que sur ma vue de profil, je voyais mon angle de coupe dans l'épaisseur du panneau mais en fait, je m’aperçois maintenant que je ne vois en VG que l'angle de la charnière. Pour bien visualiser l'angle, il suffit d'augmenter l'épaisseur.
Donc ce travail est à faire 3 fois pour visualiser tous les angles. En projetant la vue de profil rabattue en vue horizontale, j'ai mon panneau triangulaire en vraie grandeur.
Ça marche bien pour le triangle coincé entre des plans orthogonaux (en vert). Mais mon intuition me dit que mon épure est fausse concernant le triangle de droite (en rouge).
Je m'en vais maintenant lire le pas à pas. (Je reviens avec mes questions lol ^^)
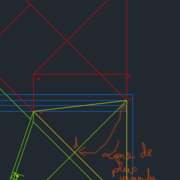
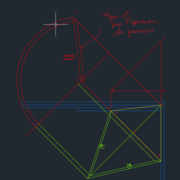
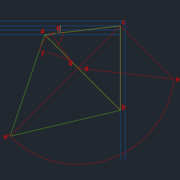
Après lecture de la SOLUTION 1 : Je me réponds tout seul, dans mon triangle vert, isocèle, la ligne de plus grande pente est l'axe de symétrie du triangle.
Dans le second cas, (triangle rouge) je n'ai pas pris la ligne de plus grande pente.
Voici donc la "correction" en rose hachuré.
En espérant que ce soit juste.
Et en fait, pas de besoin d'effectuer d'autres rabattements : on peut trouver les angles de corroyages par coupes rabattues.
Bonbonveronbi a écrit :
Je confirme !
En fait, j'ai compris le raisonnement mais pas le tracé. Et ce dès le début : quelle est la hauteur prise pour tracer le point e ?
Autre question concernant l'angle de corroyage : la manipulation décrite doit être faite sur chaque arrête, non ?
Alors dans la seconde méthode dc est la ligne de plus grande pente tracée en plan Tracé en jaune. Le point c est le sommet du triangle qui à une hauteur (on dit une cote) que l'on porte en e. Il en résulte que ce est la hauteur ou tu veux que ton panneau arrive. De est la vraie grandeur de la ligne de plus grande pente. de te permet de faire le rabattement du triangle en vraie grandeur en effet de est égal a de' en atelier on se passe du rabattement avec un compas on le fait à la pige ou au mètre. Pour l'angle de corroyage dans le cas présent il faut le faire sur les deux arêtes car tu as une pente sur l'un des cotés. L'angle de pied lui est pris en cde
Je pense que c'est le terme hauteur qui me perturbe.
La hauteur d'un triangle est la ligne coupant un sommet et rejoignant le côté opposé à angle droit.
En prenant cette définition, la hauteur du triangle abc, c'est dc, la ligne de plus grande pente.
le point e est arbitraire en fait, tu le places directement sans traçage, on part du principe que la hauteur (la côte) est une donnée connue ?
Sinon, je l'aurais bien prise sur la projection frontale mais tu ne l'as pas dessinée.
oui tu as raison la hauteur de abc c'est dc la ligne de plus grande pente .
Le point e est donc arbitraire si tu veux c'est la hauteur ou l'on veux que finisse le panneau la cote c'est toi qui la donne , je dessine pas la projection frontal car elle est pas utile , dans la première solution elle est présente. La première solution permet d'assimiler le principe , après on peux user de raccourci.
Alors c'est un peu abstrait mais une fois assimilé cela permet d'aller beaucoup plus vite que la perche .
Bonbonveronbi ah super merci. C'est vraiment ce point E qui me gênais.
Dans le cas cité dans mon pas à pas sur la reconversion, j'avais pu mesurer toutes les arrêtes en vraie grandeur. Mais ça suppose de fabriquer l'ouvrage étape par étape de et de finaliser le plan au fur et à mesure : ça se fait mais on peut mieux faire.