Ce pas à pas présente un projet en cours de réalisation.

Il y a quelques années, le PAG m'avait demandé d'animer une formation dans les villages du haut Maroni dont le thème était l'introduction au travail du bois à l'électroportatif. Connaissant personnellement la plupart des participants, j'avais une idée du faible niveau de scolarisation de certains et j'avais parsemé les séances de quelques techniques sans mesure.
Je vous les présente ici, me disant que ça pourra toujours servir.
Liste des articles
- Tracer le centre d'un segment et sa perpendiculaire
- Division d'une pièce en parts égales
- Trouver le centre d'un cercle
- Diviser un angle quelconque et deux angles égaux
- Pythagore 1: tracer un angle droit avec une règle non graduée
- Pythagore 2
- Un cercle qui passe par trois points
- Un cercle dans un triangle
- Perpendiculaire en bout de segment
- Tracer des parallèles
Tracer le centre d'un segment et sa perpendiculaire
Prenons un segment de longueur inconnue.
Ouvrir le compas plus grand que la moitié du segment (à vue d'oeil)
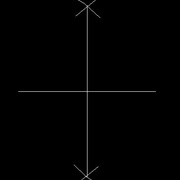
Placer la pointe du compas sur une extrémité du segment et tracer un arc de cercle au dessus et en dessous
Placer la pointe du compas sur l'autre extrémité, sans modifier son ouverture, et répéter l'opération (image 2)
Relier les 2 intersections ainsi créées. Le nouveau trait divise le segment de départ en 2 et, en plus, est perpendiculaire à celui-ci. (image 3)
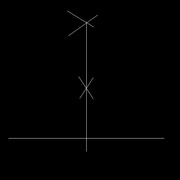
Si, maintenant, on ne peut pas tracer des 2 côtés (bord d'un panneau, par exemple):
Ouvrir le compas, placer la pointe sur une extrémité du segment, tracer un arc de cercle
Sans modifier l'ouverture du compas, répéter l'opération à l'autre extrémité du segment
Modifier l'ouverture du compas et répéter les deux opérations précédentes (image 4)
Tracer une ligne qui passe par les deux intersections et qui rejoint le segment de départ. Cette ligne le divise en deux et lui est perpendiculaire.
Division d'une pièce en parts égales
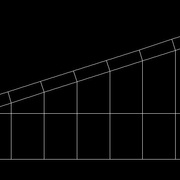
Vous êtes amené à diviser une pièce de bois en parts égales, mais la division ne donne pas de nombre rond, comme une division par 7, par exemple, ce que je prends dans l'exemple ci dessous.
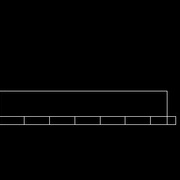
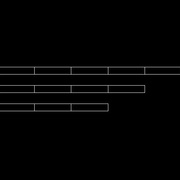
Sur une seconde pièce de bois, tracer 7 marques, de manière que le total des 7 marques soit plus grand que la pièce à diviser (image 2) Ici, il suffit de prendre des multiples de 7.
Aligner le départ de la seconde pièce et la première.
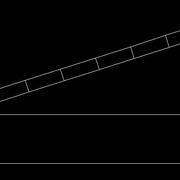
Aligner la dernière marque de la seconde pièce avec le bout de celle à diviser (image 3)
Il ne reste plus qu'à projeter et tracer à l'aide d'une équerre les divisions de la seconde pièce sur la première (image 4)
Comme l'idée de départ est de travailler sans mesurer, on peut aussi reporter 7 fois une longueur (donnée par un morceau de tasseau) sur la seconde pièce. L'intérêt est que cette longueur à reporter est quelconque, pas besoin de la connaitre.
Trouver le centre d'un cercle
On a tous du, un moment ou un autre, percer une pièce ronde en son centre, sans savoir où est exactement le centre du cercle.
Voici une méthode très simple pour le trouver.
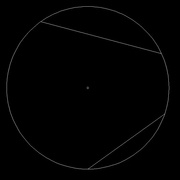
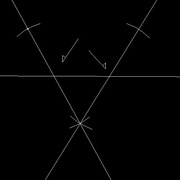
Tracer 2 segments quelconques dans le cercle, l'important est qu'ils ne soient pas parallèles (image 2)
Sur chacun de ces segments, tracer une perpendiculaire qui passe en son milieu (images 3 et 4)
Le point d'intersection des ces perpendiculaires donne le centre du cercle
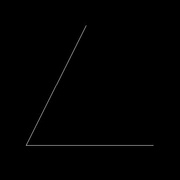
Diviser un angle quelconque et deux angles égaux
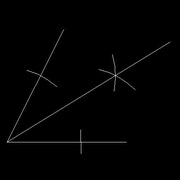
Prenons un angle quelconque (image 1), ça marche aussi pour un angle droit à diviser en 2X45°, bien sûr.
Ouvrir le compas, placer la pointe sur le sommet de l'angle et tracer 1 arc sur chaque côté de l'angle (image 2)
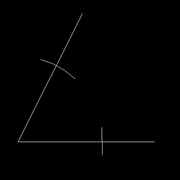
Placer la pointe du compas sur la première intersection et tracer un arc à l'intérieur de l'angle.
Faire de même sur la seconde intersection (image 3)
Tracer le trait qui part du sommet et passe par l'intersection des 2 arcs à l'intérieur de l'angle.
C'est fait !
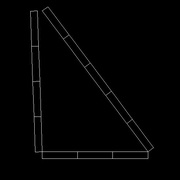
Pythagore 1: tracer un angle droit avec une règle non graduée
On a tous vécu (ou subit pour certains) le théorème de Pythagore au collège. Il est pourtant indispensable dans la construction, surtout quand les longueurs en jeu atteignent les limites des outils de mesure ou bien rendent l'utilisation d'une équerre complétement aléatoire.
Petit rappel (vous me pardonnerez cette toute petite séance théorique, mais elle me parait essentielle)
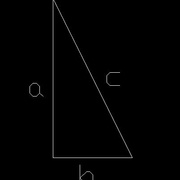
Dans un triangle rectangle comme celui de l'image 1, on a:
a²+b²=c²
Si pour un triangle donné, on effectue l'opération ci-dessus et que le résultat à gauche du = et le même que celui à droite, alors, on a la garantie que l'angle entre a et b est angle droit.
Par exemple, on a fait un tracé avec
a = 19.6
b = 14.7
Comment vérifier que l'angle est droit ?
a² = 384.16
b² = 216.09
a² + b² = 384.16 + 216.09 = 600.25
On va calculer la racine carrée de 600.25 = 24.5 C'est la valeur calculée pour avoir un angle droit
Maintenant, sur le tracé, on mesure c
Si c = 24.5, alors, on a bien travaillé et l'angle est droit. Si la mesure est différente, l'angle n'est pas droit.
Bien sur, avec les racines carrées, on se retrouve avec des chiffres après la virgule dans tous les sens, et c'est vite pénible. Mais il existe des nombres sans virgule pour lesquels le théorème s'applique: c'est la combinaison 3/4/5
Si, dans le triangle de l'exemple, a = 4, b = 3 et c = 5, ça marche facilement, limite sans calculatrice:
3² + 4² = 5²
9 + 16 = 25
Le plus intéressant dans tout ça, c'est que ça marche aussi avec les multiples identiques de 3/4/5. Par exemple, je multiplie tout par 7 et j'ai 21/28/35 et
21² + 28² = 35²
441 + 784 = 1225
Et encore plus intéressant, c'est que ça marche avec n'importe quelle longueur, du moment qu'on la reporte 3, 4 et 5 fois: un clou sans tête, une tige de bambou, une cigarette,...
Maintenant, l'application, avec comme outils un crayon et quelques tasseaux bien droits.
On choisit d'abord un tasseau qu'on gardera comme pièce de référence, ou bien on ouvre le compas à une longueur quelconque.
Sur un tasseau, reporter 3 fois la longueur du tasseau de référence
Sur un second, reporter 4 fois la longueur
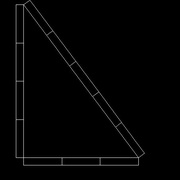
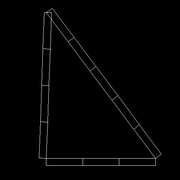
Sur un troisième, reporter 5 fois la longueur (image 2)
Ensuite, placer les 3 tasseaux en triangle (image 3), ça y est, on a un angle droit
Ceci peut également servir à vérifier un angle droit:
Placer les tasseaux 3 et 4 sur les bords de l'angle. En plaçant le tasseau 5, on a trois cas de figure:
image 3: l'angle est droit
image 4: l'angle est trop ouvert, il est supérieur à 90°
image 5: l'angle est trop fermé, il est inférieur à 90°
Je me sers essentiellement de cette méthode quand je dois mettre à format un plateau de table trop grand pour aller sur le chariot de la combinée et que je dois utiliser la scie portative et son rail. Le résultat est toujours au rendez-vous.
C'est également avec cette méthode que je vérifie que le guide de la scie, sur le chariot, est bien perpendiculaire à la lame: je passe un panneau, le plus grand possible (plus c'est grand, plus l'incertitude des outils de mesure se réduit et plus c'est précis) à la scie, je le tourne d'un quart de tour pour que le chant fraichement coupé se retrouve contre le guide et je repasse à nouveau le panneau à la scie. Je mesure la longueur des deux chants coupés, la diagonale et j'utilise Pythagore pour vérifier et faire quelques ajustements. Très efficace.
Pythagore 2
Une autre propriété des triangles rectangles, mais je ne sais plus si ça découle du théorème de Pythagore, enfin bon, ça fera bien l'affaire.
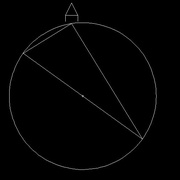
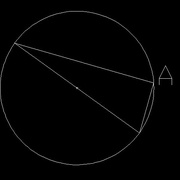
Tracer un cercle et son diamètre (image 1)
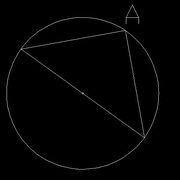
Tracer deux traits qui partent des extrémités du diamètre et qui se rejoignent sur le cercle (images 2, 3 et 4) A chaque fois, l'angle A est un angle droit.
Voici donc un autre moyen de tracer un angle droit à la règle et au compas.
Un cercle qui passe par trois points
Quand on a trois points, peu importe comment ils sont dispersés, il y a toujours un cercle qui passe par ces points, sauf s'ils sont alignés.
Voici une méthode pour tracer ce cercle, et par extension, tracer un cercle qui passe par les sommets d'un triangle.
Relier les points par des traits, le troisième trait n'est pas nécessaire, c'est juste pour montrer l'exemple avec un triangle (image 2)
Sur 2 traits, tracer une ligne qui passe par le milieu et qui est perpendiculaire (image 3)
Le point d'intersection donne le centre du cercle (image 4)
Un cercle dans un triangle
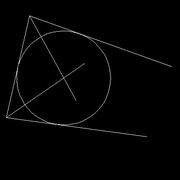
Il est parfois utile de pouvoir tracer un cercle qui est dans un triangle et touche les trois côtés.
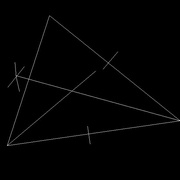
Pour ce faire, il faut diviser les angles du triangles (2 suffisent) en 2 angles égaux, grâce à la méthode vue précédemment (images 2 et 3) L'intersection de ces 2 bissectrices donne le centre du cercle
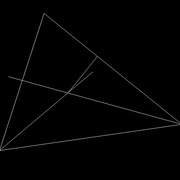
Ensuite, à partir d'un côté au choix, on trace la perpendiculaire à ce côté et qui passe par le point d'intersection (image 4)
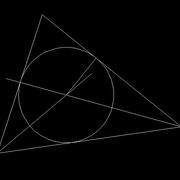
Il reste à tracer le cercle dont le rayon en plaçant la pointe du compas sur le centre et l'autre là où se croisent la perpendiculaire et le côté (image 5)
Cette méthode peut aussi servir lorsqu'on a une figure ouverte (image 6), on peut tracer un cercle qui touche les 3 côtés (image 7)
Perpendiculaire en bout de segment
Comme demandé plus haut, voici comment tracer une perpendiculaire en bout de segment
Tracer une perpendiculaire au milieu du segment (image 2), ça a été vu plus haut, je ne refais pas ici le traçage
Tracer une droite quelconque qui passe par l'extrémité du segment initial et qui coupe la perpendiculaire (image 3)
Placer la pointe du compas sur l'intersection de la droite et de la perpendiculaire, ouvrir le compas pour que l'autre pointe arrive à l'intersection du segment et de la droite et marquer cette droite de l'autre côté (image 4)
Relier la seconde extrémité du segment à cette nouvelle intersection, on a un angle droit (image 5)
Tracer des parallèles
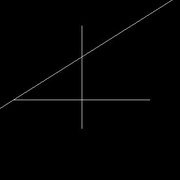
Soit la droite parallèle doit passer par un point précis soit non, dans ce dernier cas, il suffit de placer un point n'importe où.
Tracer deux droites quelconques qui se croisent, mais une des deux doit passer par le point (image 2)
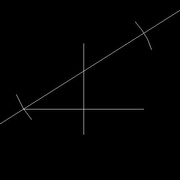
Placer la pointe du compas à l'intersection d'une des droites (flèches image 3) et du trait d'origine et ouvrir le compas jusqu'au point d'intersection des droites. Tracer de l'autre côté un trait sur la droite.
Faire la même opération avec la seconde droite, il faut, bien sûr, modifier l'ouverture du compas.
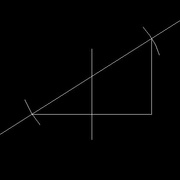
Relier les intersections, la nouvelle droite est parallèle à la première (image 4)
Si, maintenant, on doit tout tracer du même côté du trait d'origine:
Tracer une droite quelconque qui passe par le point (image 5)
Placer le compas sur le point, ouvrir jusqu'à l'intersection et tracer un trait sur la droite de l'autre côté (image 6)
Relier le nouveau point d'intersection au trait d'origine par un segment quelconque (image 7)
Trouver le milieu de ce nouveau segment, ça a été vu plus haut, je ne fait aucun traçage pour ça ici.
Tracer une droite qui passe par le point et le milieu du segment (image 8)
Ce pas à pas présente un projet en cours de réalisation.































Discussions
intéressant de mettre le fondamentaux de tracés géométriques ici !!!
Bon voilà, il m'en reste 2 à ajouter: tracer un cercle qui passe par 3 points et tracer un cercle inscrit dans un triangle, ce sera pour ce soir ou demain. Sinon, c'est collaboratif, tout ce que vous avez à ajouter sur les tracés est le bienvenu !
il ne te restera plus que les tracés des polygones !!
Ha ha, les polygones... ça devient vite très complexe à tracer. Mais oui, je vais y penser.
Tchabissi c est un peu la base si tu veux !! faut allez au bout ;)
Merci Tchabissi !
Message à part. Mais, il faudrait vraiment travailler pour que le site arrive à mettre plus en avant vos formidables travaux de documentation. Ouvert aux idées.
hello Boris , j y ai pensé figure toi !! tu laisse en pas à pas (cela draine beaucoup de monde , par contre tu fait une bannière qui r envoie dans une bibliothèque savoir faire ,gestes , théories , bref tout ce qui ne serait pas pratique pure !!
celui qui ferais un pas à pas devrais avoir à choisir pour éditer concret ou explication .
bon c est brouillon pour l instant et je n ai pas la logique informatique .
Ca c'est vraiment une excellente idée, a terme, ça pourrait faire une espèce d'encyclopédie avec de la théorie et de la pratique, je pensais par exemple aux piges d'équerrage, à la prise de cote dans des situations plus complexes,...
Tchabissi dans pas à pas , rubrique biblio , savoir faire , construction concrète
parole au boss du site ;)
L'idée de la rubrique me parait très bien, on ferait la différence entre une réalisation et de la théorie.
Simple et efficace
Il y a quelque chose de très interessant qui mijote par ici !
il y aussi le tracé d'une perpendiculaire en bout de segment toujours avec la règle non graduée et le compas
le tracé d'un arc de grand rayon... connaissant la corde et la fleche avec 2 lattes clouées qui coulissent sur 2 clous à la fois ... 3 arcs differents sur mes tables gigognes donc 3 montages un tracé tres tres peu connu appris en 1959 par mon prof de charpente bois...
Bon, ça fait une demi heure que je suis sur le schéma, on va voir si j'ai compris.
Tchabissi oui c est ça tu as tout compris , souvent utilise en charpente et en arpentage .
Ce qui est par contre plus connu, c'est ce cas de tracé avec l'intérieur d'une équerre alsacienne et le diamètre du demi-cercle obtenu est celui de la distance entre les 2 pointes (corde)
Tchabissi realisation pour comprehension j'en ai d'autres en preparation je n'utiliserai plus
Bonjour, merci pour ce partage fort intéressant
La corde à 13 noeuds est très pratique aussi pour retrouver des angles droits.
Cordialement
Petite video en lien Mathématique et géométrie médiévale
Excellent, c'est une bonne vidéo. Et puis, Pythagore, il peut dire ce qu'il veut, nous on va aller vérifier !
Bonjour, quel est le logiciel utilisé pour représenter tous ces tracés ?
Est-ce que ça pourrait être le même que celui utilisé sur ce site :
apprendrelacha...te.blogspot.fr/