Ça fait quelques semaines que j'essaie (pas à plein temps, je vous rassure), de dessiner un heptagone régulier à la règle et au compas.
Je suivais des méthodes trouvées dans des bouquins de menuiserie qui ont une partie géométrie. Et dernièrement je m'y suis remis avec la méthode de Léon Jamin (qui était la même que d'autres déjà essayée).
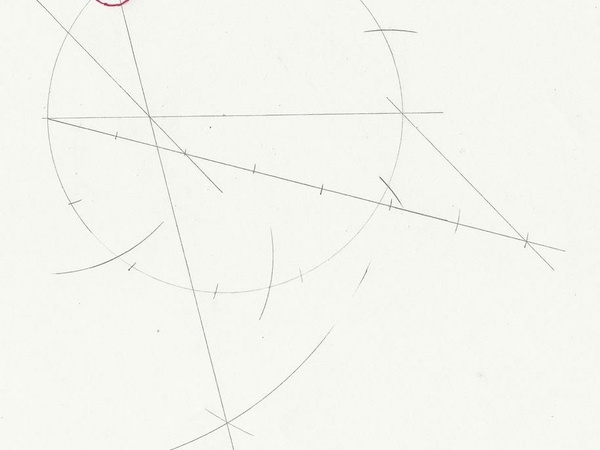
J'ai travaillé ma précision, acheté un nouveau compas, tout tracé au porte mine 0.3mm, construit les parallèles au lieu des les reporter à l'équerre et à la règle, etc... Toujours la même différence. (entourée en rouge sur le dessin).
Bref, tout ça pour apprendre que c'est impossible... 
Ils ne disent jamais dans les méthodes que c'est un résultat faux mais approchant.
Voilà, je voulais le dire.
Et vive la salade de fruits.



Discussions
Pour ceux qui veulent aller plus loin, voici la méthode de construction de l'heptadécagone (j'ai appris un nouveau mot à mon correcteur d'orthographe ^^) régulier (64 étapes).
Très intéressant! Merci!
avec plaisir :D
trente six seb En fait, c'est pour cela que les 7 nains ont été si content de voir arriver Blanche Neige. Avant, ils se battaient toujours pour partager la tarte. A 8, c'était plus facile.
hou elle est belle celle là! (mais pas facile à placer...)
ced21 Si si, cela permet ensuite d'introduire le théorème de Gauss Wantzel, les nombres premiers de Fermat et même le théorème de Fermat, le truc qu'il avait écrit sur la marge d'un bouquin et qu'on a enfin réussi à démontrer 3 siècles après...
ben oui ça marche, ce soir ou avait une boite de chocolats octogonale. J'ai parlé de l'heptaghone imopossible à tracer.
Si j'avais lu l'explication de Blanche Neige par Kentaro, j'aurais pu enchaîner.
c'est bien la conclusion à laquelle j'étais arrivé lors d'une soirée !!!


Il est vrais que pour tracer un heptagone, la construction géométrique est seulement approchante !!
Mais en épure (surtout au réel parfois de grande dimension) , en charpente ou en menuiserie , la construction géométrique, s'accompagne chaque fois d'un cheminement proche en proche de réglage du compas ,car même sur du tracé considéré juste ,on ne tombe pas chaque fois pile aux bon points !
Ex : Essaye de tracer du premier coup un hexagone, tu verra que ce n'est pas évident de tomber pile en reportant 6 x le rayon !!!
En effet... pour dessiner un hexagone, iL faut au moins faire en deux parties, reporter 3 fois d'un coté, et reporter 3 fois de l'autre. Dans ce cas, on ne reporte pas les erreurs 6 fois. Mais même ainsi, on fait des erreurs...
Sinon, pour l'heptagone, il faut quand même relativiser... L'erreur "theorique" est de 0,8677/0,866 , soit 2/1000...
IL est donc fort possible que si trente six seb n'arrivait pas à dessiner son heptagone, ce n'était pas à cause de l'impossibilité théorique, mais à cause d'erreurs de manip...
Si ! l'Hexagone j'ai réussi ! du premier coup. Mais en fait j'ai vraiment pris mon temps pour être super précis (après tous les essais sur l'heptagone).
La méthode qui est décrite est appelée Bion. Elle produit une erreur. Apparemment,; il exsite une autre méthode, dite Tempier qui est plus juste.
Plus de détail ici.http://villemin.gerard.free.fr/GeomLAV/Cercle/Bion.htm
La méthode Bion est celle-ci (voir photo) : tracé à partir de la deuxième division du diamètre.
La méthode Tempier trace à partir de 2 divisions à gauche du milieu du diamètre.
Kentaro ben non j'ai toujours l'erreur approximative comme dans le dessin dont je parle dans le post initial (et que j'ai oublié de publier).
trente six seb La methode donnée dans Wikipédia (chap "constructions approchée), donne une erreur de 2/1000:
fr.wikipedia.o.../wiki/Heptagone
Ah oui, mais je n'ai essayé qu'une seule méthode (celle décrite juste au dessus par la division du diamètre en autant de parties égales que l'on souhaite de côtés. C'est censé être une méthode qui permet de faire tous les polygones.
La méthode de wikipédia est bonne. Mais l'erreur n'est pas négligeable. 1er essai, j'arrive à une longueur de côté de 46 mm, 2/1000ème, ça fait 1/10e d'erreur par côté, soit 7 dixièmes. + l'à peu près du dessinateur : erreur 2 mm.
Deuxième essai, j'ai dû compenser l'erreur en prenant mes repères. J'arrive à un poil de c.. de philosophe grec de la bonne longueur.
Mais bon, je cherche la recette idéale. Sinon, il faut uitiliser la méthode de sylvainlefrancomtois : avoir une première approche puis faire par tâtonnements.
Pour ceux qui ont besoin de faire les calculs mais qui sont feignants, on peut calculer les côtés à partir du cercle inscrit ou du cercle circonscrit dans la pager de calcul suivante. Ça peut servi, du coup je le partage.
La longueur du coté d'un heptagone est tout simplement 2 x sin (Pi/7) multiplié par le rayon du cercle circonscrit.
Ou encore plus plus simple: c'est Rayon x 0,87767
Ah ? Je te crois bien volontiers. Il y a plus simple alors.
bonjour
se cultiver c'est cela
comprendre que certaine chose sont possible et d'autre pas d'ou l'utilité de faire de la géométrie
mais est il bien utile de faire une telle construction lorsque un calcul simple permet d avoir un résultat maintenant vous pouvez vous attaquer a la quadrature du cercle
mes amitiés au gens qui cherchent et aussi et surtout à ceux qui trouvent la solution
etienne