C'est ballot ça !
Je n'ai pas Sketchup ni autre logiciel et donc les feuilles sont forcément limitées dans l'espace.
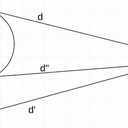
Il est arrivé à tout le monde lors d'un tracé de ne pouvoir joindre 2 droites car leur intersection était hors du champ de la feuille.
On peut imaginer aussi d'avoir un mur dans la vraie vie qui nous empêche de tracer.
Cette intersection nous était nécessaire pour tracer une droite à partir d'un point.
Question : Comment fait on ?
Il s'agit d'un petit concours où il n'y a rien à gagner sauf le plaisir d'apprendre des trucs.
J'ai des éléments de réponse depuis 5 minutes !
Mais je trouvais le problème intéressant.
A vous de jouer ;-)
12 réponses
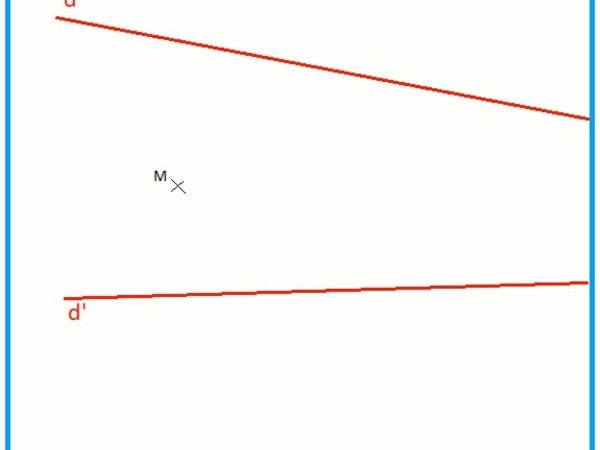
- On trace une droite verticale, passant pas M, coupant D en A et D' en A'
ON mesure le rapport MA/MA'
- On trace une autre droite verticale, vers la droite de la page, parallèle à la précédente, coupant D en B et D' en B'.
On définit N sur cette seconde droite, tel que NB/NB' = MA/MA'
La droite recherchée passe par MN.
Cela doit être un dérivé de Thales.
( En fait, il faut le voir comme un problème de dessin de perspective. Les 3 droites qui se rejoignent sur le dessin représentent en perspective 3 droites parallèles. Sur cette perspective, les segments MA et MB sont en fait égaux, de même que MA' et MB'. La perspective conserve les rapports.)
Edit: Démonstration:
ON a AM/AO= BN/BO (=) AM/BN =AO/BO
et A'M/A'O= B'N/B'O (=) A'M /B'N = A'O/B'O
et AO/BO= A'O/B'O
donc AM/BN = A'M/B'N
donc AM/A'M = BN/ B'N
CQFD !!! J'ai gagné! (si je ne me suis pas planté...)
- Edit: Méthode pour reporter les rapports sans mesurer, par la géométrie seule:
Il n'y a pas de méthode qui utilise une droite quelconque passant par M. J'essaie de tracer ce que tu as décrit pour le confirmer.
Par contre, il faut "mesurer" le rapport, ce qui n'est pas de la bonne géométrie de tracé. Il doit y avoir une méthode pour trouver geométriquement le rapport et le réutiliser sur la seconde droite.
Effectivement ça ne semble pas marcher.
- si j'ai bien compris ce que tu voulais dire
- si mon tracé est assez précis, ce qui n'est pas certain
trente six seb sur ton dessin, les droites ne se rencontrent pas à droite. Tu ne peux pas avoir le bon résultat
Je n'avais pas vu les commentaires de Kentaro et Boris Beaulant
Du coup ça doit venir de mon tracé. Et si je ne l'ai a
pas dans les méthodes données, c'est sûrement parce que les réponses que j'ai ne se trouvent que par le tracé. Pour certains uniquement à la règle d'ailleurs.
Kentaro au fait, quand tu dis verticale, c'est une vraie Verticale ? avec un V majuscule ? et qui tient debout avec un fil à plomb et tout et tout ?
(j'ai pris une droite quelconque qui va de haut en bas)
Bon, avec des Vraies verticales, ça marche encore moins bien... :(
aucune idée si ta justification mathématique est juste...
Je crois que tu as fait en sorte que NB/BB' = MA/AA' alors que Kentaro veut faire NB/NB' = MA/MA'
(Ta valeur de 8,45 correspond à AA' et non à MA')
oui mais si le rapport du petit côté sur le grand est constant alors le rapport du petit côté sur le tout est constant aussi non ?
ça me simplifiait les calculs ;)
trente six seb Pas faux... Et si tu mesures au niveau de ton axe vertical qui représente la limite de ta feuille, les rapports sont toujours les mêmes ?
Edit: pardon, clairement non, ça se voit à l'oeil. C'est q'uil y a effectivement un problème avec cette méthode... En fait ça permet juste de créer une droite perpendiculaire aux deux verticales j'ai l'impression ^^
Alors là, j'avoue que je ne sais plus trop. Les tracés simples de géométrie ça va, la trigo un peu et après c'est plus compliqué pour moi. ;-)
Les deux droites dites "verticales" sont en fait quelconques. Il faut simplement qu'elles soient parallèles.
trente six seb la trigo un peu et après c'est plus compliqué pour moi.
Pas de trigo, juste des rapport de longueur avec le théorème de Thales.
OK, c'est ce que j'avais compris au début.
C'est marrant mon premier dessin était très proche avec des quelconques et le deuxième avec des verticales était plus éloigné.
Il faudrait trouver une méthode de report des rapports au compas pour être plus précis. En mesurant, c'est forcément plus imprécis.
Mes chers amis, vous n'êtes vraiment pas loins de la solution que j'ai vue. Seulement il faut pouvoir se passer de mesure et de calcul.

trente six seb dneis J'ai trouvé la méthode pour reporter les rapports, sans avoir à mesurer. J'ai édité ma réponse plus haut.
Je suis certain de ma méthode à 99% (mais j'ai pu me tromper...  )
)
Bon, je veux bien publier une réponse, mais j'attends qu'on me l'autorisation de trente six seb pour savoir si c'est le bon moment 
Et puis bon, c'est honteux mais j'ai ouvert un bouquin et je n'ai rien inventé 
Vous semblez tourner autour du pot...
Alors ? Ça vous a occupé à ce que je vois. 
Kentaro je ne comprends pas ta méthode pour reporter le rapport. C'est la 5 ème figure qui me perd. Tu mets les 2 rapports sur la même verticale ?
dneis oui bien sûr, tu peux y aller 
Kentaro oui il y a plein de méthodes, il faut que je vérifie mais je crois en avoir trouvé une autre
trente six seb L'hypoténuse du triangle "vertical" de droite (la pente) permet de reporter le rapport. C'est un peu subtil. Mais ça marche, fais moi con-fi-ance... ;)
Sa marche bien j'ai vérifier plusieurs fois pour comprendre le premier jet de Kentaro avant les étapes comme je le disais le seul soucis que lon peut trouver c que lorsque l'angle est ouvert le cercle risque de sortir de la feuille
Mais bon avec un logiciel de dessin pas de soucis ... enfin avec un logiciel de dessin la feuille n'a pas ee limite donc le problème n'existe pas 
Hello.
Tu trace deux parallèles a d et d' passant par M , la parallèle a d' croise d donne le point A , la parallèle de d croise d' et donne B. Tu relie A et B , le centre de cette droite te donne le deuxième point de ta droite.
Ça fonctionne.
Mais on n'est pas certain d'avoir à tous les coups les points A et B à l'intérieur des droites bleues délimitant l'espace disponible pour le tracé.
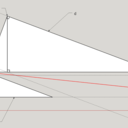
Et non ce n'est pas bon non plus (la ligne rouge). 
la ligne verticale est la limite virtuelle de la feuille
la droite au crayon de papier est tracée suivant la méthode de Boris Beaulant
Du coup, effectivement, ça marche ! (c'est la ligne bleue).
Effectivement ça peut être en dehors de la feuille.
Bravo à Stef64 et à Boris Beaulant (pour avoir insisté et fait la démonstration)
J'ai cherché un peu, puis décidé de trouver dans un livre 
Solution simple, rapide, efficace, précise.
Ah, mais c'est bien sur!!
Simplicité radicale.
Punaise, il faut vraiment être un génie absolu pour trouver ça...
Bretzel a trouvé une solution valide basée sur les propriétés de la symétrie centrale en faisant une espèce de nœud papillion.
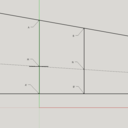
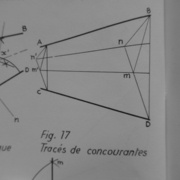
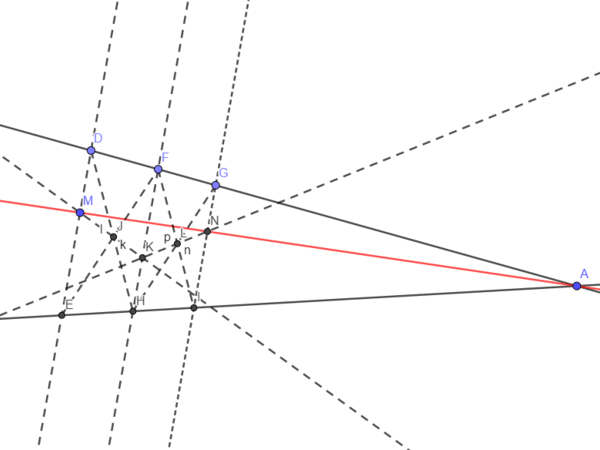
J'avais une solution similaire en tête en mettant plutôt deux "noeuds-pap'" en série, et en utilisant seulement un fil a plomb et une règle. Pour commencer, on trace une verticale passant par M puis 2 autres verticales à des endroits quelconques. Il suffit de tracer la figure
Comme la symétrie centrale conserve les proportions, DM/DE = GN/GI et on montre assez facilement avec le théorème de Thalès que (MN) passe par le sommet de l'angle formé par nos deux droites.
edit: Si vous avez la flemme de vous appliquer, il suffit de deux droites parallèles (GI) et (DE). le segment [FH] peut faire n'importe quelle longueur et être à peu près n'importe comment (il faut juste que [DE] et [GI] admettent une symétrie centrale par rapport à [FH])
Wahou !!!! Si je ne fais pas d'erreur, cette méthode s'appelle "la construction par polaires réciproques" !
D'après Jean Henri Lambert 1728-1777.
Well done !!! 
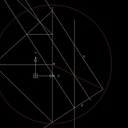
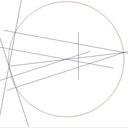
La droite recherchée d" passe aussi par l'intersection C des deux droites d et d', donc les droites d, d' et d" sont trois rayons du cercle centré sur C et passant par M. Je ne joue pas, je suis dessinateur industriel.
Pascaltech Je sens qu'il y a un truc, mais j'ai du mal... tu ne veux pas nous en dire un peu plus ?
Oui, sans problème, bien que je ne connaisse que le point de départ, je n'ai pas encore tracé.
Une règle en géométrie : il n'y a pas beaucoup de choses à connaître :
1 : le triangle rectangle de Pythagore
2 : les droite remarquables du cercle :
2.1 le rayon
2.2 le diamètre
2.3 la tangente
2.4 la corde (la sécante infinie porte le segment corde fini)
2.5 la flèche (je ne l'utilise que très rarement)
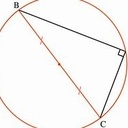
2.6 le triangle inscrit dans le cercle dont l’hypoténuse est confondu avec son diamètre.
et toutes les règles qui en découlent.
Ces connaissances résolvent pratiquement 90 % des problèmes de géométrie.
Les règles qui en découlent :
a - la tangente passant par l'extrémité du rayon est perpendiculaire à celui-ci(de-même pour un diamètre, vous vous en doutez).
b - la bissectrice (droite perpendiculaire passant par le milieu d'un segment) de la corde passe par le centre du cercle.
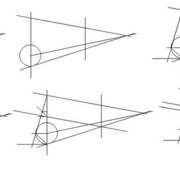
c - tout point du cercle relié aux deux extrémités d'un diamètre forme un triangle rectangle(2ème et 3ème schéma).
Les règles a et b doivent être suffisantes pour résoudre ce problème.
Les tricheurs gagnent 1/2 point. 
Ben, pour trouver le centre du cercle (sans logiciel ad hoc) passant par les 3 points M, A et B, il faut bien tracer les perpendiculaires passant par le milieu des segments MA et MB (les médiatrices), non ?
Oui, mais considère que c'est hors de la feuille et que tu ne peux pas tracer le centre.
A et B sont à l'intersection des cordes et des médiatrices mais ne sont pas sur le cercle. Ce sont les symétriques de M, M' et M" par rapport aux droites d et d' qui sont sur le cercle.
Positionne les point A et B comme précédemment positionnés pour être sûr que l'on parle des mêmes points.
En fait, il n'est pas indispensable de tracer le cercle que j'ai mis. Il suffit d'avoir son centre, qui est bien sur la feuille. Et ce centre, on le trouve en traçant les deux médiatrices de MA et MB.
Tu ne peux pas tracer le cercle car le centre est en dehors de la feuille. Prends le problème depuis le début.
Redonnes un tracé avec les points M, A et B, ça ne colle pas.
Pascaltech On ne doit pas parler de la même chose... Tu as regardé mon schéma ? il marche, non ? Le centre du cercle est bien au milieu de la feuille, pas en dehors.
benjams En fait, je recherchais le centre du cercle qui passe par M, et les projections orthogonales de M sur d et d' (A et B).
Pour cela, je trace les deux médiatrices de MA et MB, pour trouver le centre du cercle.
Et bien sur, c'est la même chose que de faire l'homothétie de rapport 1/2.
Désolé, je ne trouve pas, je me trouve rouillé.
J'ai essayé dans cette voie, en reliant les points extrêmes M' et M" qui sont sur le cercle, cela donne un nouveau segment dont la bissectrice va au cente, mais je ne trouve pas.
M' et M" sont les symétriques de M par rapport aux droites d et d'.
Tu ne dois pas tracer le centre du cercle puisque tu ne le connais pas.
Bravo !
Le rayon du cercle égal MC':
Abaisser la perpendiculaire de M sur AB :
Tracer un rayon de valeur quelconque centré sur M venant couper AB en deux points M1 et M2.
Planter le compas en M1 et M2 et reporter M de l'autre côté de AB : M3.
Tracer la perpendiculaire à AB en reliant M et M3.
tracer le cercle dont le centre est M et passe par l'intersection de MM3 et AB.
Pour obtenir par tracé le point A' :
Tracer le milieu de MB par le tracé de la médiatrice:
A partir de M et B reporter au compas de chaque côté de MB un rayon quelconque à partir de M et B.
Ces rayons se croisent en deux points qui permettent de tracer la médiatrice de MB.
A l'intersection de la médiatrice et de MB se trouve le milieu de MB.
Tracer un cercle depuis ce point et passant par M et B, le point A' est à l'intersection de ce cercle et du cercle de rayon MC'. pfff !!!!
De même pour B'.
Prolonger BA' et AB' pour obtenir C.
Le cercle est inscrit dans le triangle ABC.
MA, MB, MC sont les bissectrices du triangle ABC.
Pourquoi cela marche ? Je ne sais pas. Un concours de circonstances ?
Pascaltech C'est presque le même principe que ce j'ai proposé plus haut, avec le grand cercle...
Ca fonctionne en utilisant le centre du cercle inscrit qui est l'intersection des bissectrices. Avec les perpendiculaire au bissectrices au sommet on arrive à avoir le le centre d'un cercle exinscrit par lequel passe la dernière bissectrice. Tout le truc étant de faire un triangle dont le centre du cercle inscrit est M.
On pourrait penser qu'on pourrait obtenir un résultat similaire avec les médiatrice et le cercle circonscrit mais ça ne marche pas, les médiatrice ne sont pas une notion "locale" contrairement aux hauteurs et encore plus aux bissectrices
Personnellement je tracerais deux droite perpendiculaires à D et D' passant par M en D1 et D1'
je mesurerais la distance D1M et D1'M j'applique un rapport par exemple la moitié et je reporte une parallèle à D et D' passant par les points D2 et D2'
l'intersection me donne la direction de la droite
Ha c'est pas mal aussi ça !
Et tu vas faire varier le rapport pour rapprocher le point si jamais il est pas dans la feuille.
et ça s'appelle comment ??? 
(c'est un mot que je connais depuis ce soit même si je crois l'avoir vu pendant ma scolarité...)
En tout cas, c'est une méthode, bravo !
alors je doit bien avouer que je ne connais pas le nom de la méthode par contre je suis à peu près sure qu'il doit y avoir moyen d'y arriver sans mesure mais mon cerveau est un peu ralenti en ses temps de télétravail 
Faire un milieu de segment sans mesure, c'est possible, oui : médiatrice au compas.
oui en effet pour le milieu d'un segment mais dans le cas du problème j'imagine bien que bien souvent la simple moitié de segment ne suffit pas à rentrer dans le "cadre" ...
trente six seb le hic, c'est qu'il faut diviser avec le même rapport sur les deux segments allant perpenduculairement vers les droites d et d'
fab83, y a toujours moyen de rediviser en 2 le nouveau demi segment avec une nouvelle médiatrice :)
C'est une Homothétie de rapport 1/2 !
Ça fait classe quand même !
On la doit à Michel Chasmes fr.wikipedia.o.../Michel_Chasles
Oh bah en fait peu importe plus on la trace proche de M plus l'intersection aura de chance de se retrouver dans la feuille cela permet juste de trouver une infinité de points D2 et D2' sans avoir à les calculés 
oui mais il faut bien que les 2 parallèles (celle de d et de d') soient tracées sur le même principe.
en fait j'ai encore plus simple et sans calcul il suffit de tracer deux droite passant par M formant D1 et D1' on trace n'importe ou une parallèle à cette droite passant par D2 et D2'
on reporte une parallèle à D passant par D2 et une parallèle à D' passant par D2' cela nous donne le point G (pour que des mathématiciens est chercher 11 méthodes différente de l'obtenir ce ne peut être que pour sa  )
)
et voilà on as notre droite
1er essai -raté !
Je tente ma chance à l'aide de la réponse de Kentaro
On trace V verticale passant par M
On mesure au compas la distance entre M et l'intersection V - d puis on trace l'arc de cercle en piquant le compas à l'intersection de d et le bord droit de la feuille (ou une quelconque autre verticale).
On fait pareil pour M - intersection Vd'
Normalement - si je ne me trompe pas  - l'intersection des deux arcs se trouve sur la droite recherchée.
- l'intersection des deux arcs se trouve sur la droite recherchée.
2ème essai -transformé!
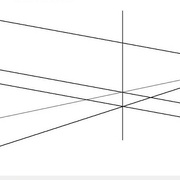
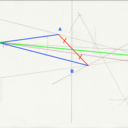
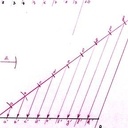
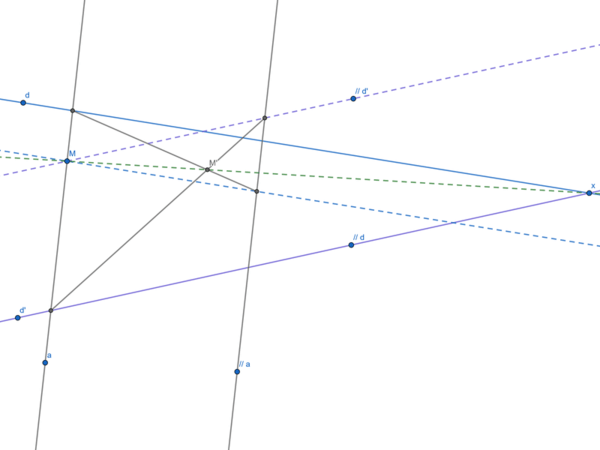
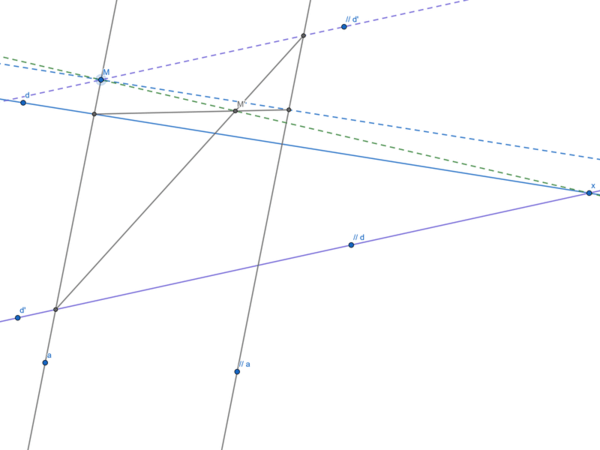
à tête reposée, cette fois-ci, modélisé sur GeoGebra (top ce programme) donc en image. En plus la solution est réalisable uniquement à la règle non graduée + compas (pour tracer les parallèles) :
on trace a (quelconque) passant par M et //a sa parallèle,
on trace //d et //d' les parallèles respectives à d et d'
on relie alors les intersections a.d, a.d', //a.//d, //a.//d' et à l'intersection de ces nouvelles droites on trouve M' le tant recherché 
Cette solution fonctionne même avec M en dehors des lignes d, d'
Je pensais verticale verticale, mais tant qu'elle est parallèle à mon "bord droit" ça devrait le faire
Oui c'est que j'avais cru comprendre, mais je ne voulais pas utiliser le terme de parallèle pour ne pas te donner de piste. Je vérifie  ...
...
Elle est jolie ta proposition, on dirait l'étoile noire !!!
Mais ça ne répond pas à la question (si j'ai bien compris ce que tu voulais dire).
Merci du test ! Tu as bien compris en tout cas.
Il y a comme un petit problème de référentiel à résoudre pour que les arcs se croisent... (avec un M plus centré verticalement ça le faisait probablement)
En reprenant le même dessin, en retraçant les mêmes cercles (en gardant leur même diamètre) mais en pointant maintenant le compas sur l'intersection cercle/droite, l'intersection des deux nouveaux cercles ne serait pas notre graal ?
eut Bretzel tu traces des novueaux cercles avec pour centre l'intersection des cercles et des droites ? Et en conservant le même rayon ?
trente six seb C'est vrai ! C'est peut-être grâce à ce tracé qu'elle a été conçue.
Ha oui pas mal aussi comme solution sans mesure .... en fait les deux sont quasi identiques même si l'approche n'est pas exactement la même
En m'appuyant sur la méthode de Stef64
Tracer deux parallèles à d et d' passant par M (droite bleue)Tracer la bissectrice de ces deux droites (droite verte) = solution = diagonale du parallélogramme "virtuel" formé par les lignes rouges et bleues
 EDIT : Ca, c'est pas bon :(
EDIT : Ca, c'est pas bon :(
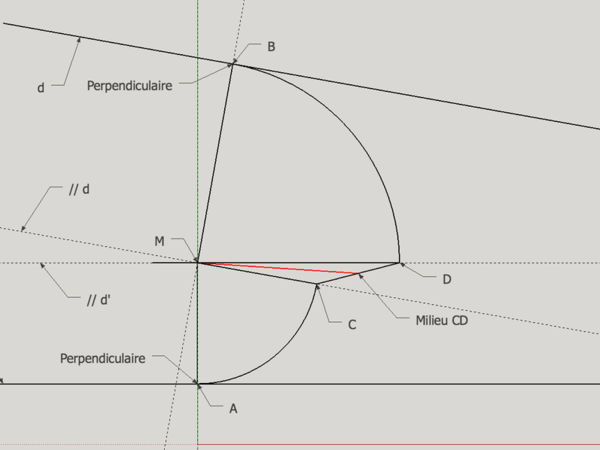
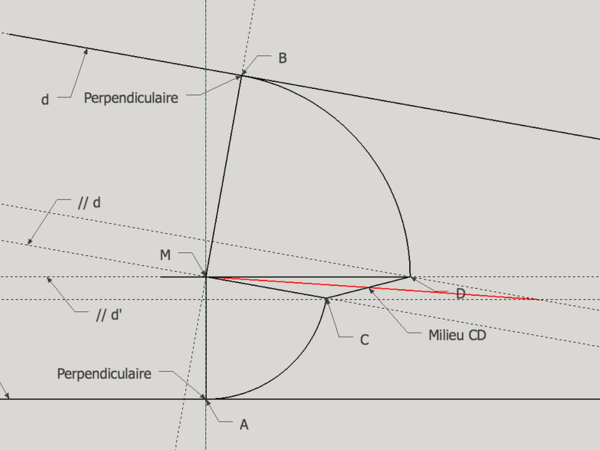
Deuxième essai :
- Tracer deux parallèles à d et d' passant par M
- Tracer deux perpendiculaires à d et d' passant par M
- Reporter au compas la longueur MA sur la parallèle de d passant par M = point C
- Reporter au compas la longueur MB sur la parallèle de d' passant par M = point D
- Tracer la droite reliant M au milieu de CD
La variante pour éviter de chercher le milieu de CD serait de refaire des parallèles passant par C et D et on retrouve le parallélogramme.
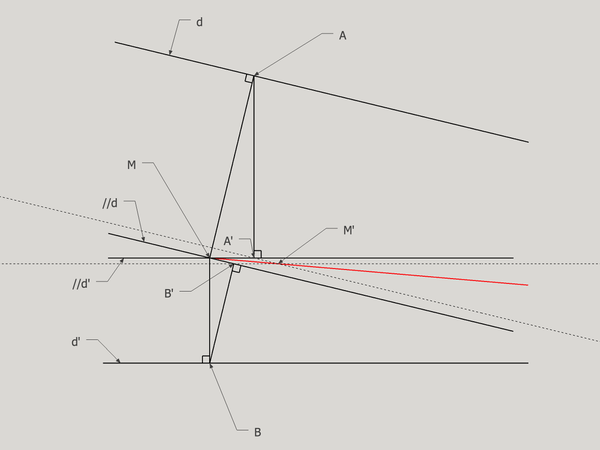
Autre solution pour arriver à un petit parallélogramme (encore plus petit) :
- Tracer deux parallèles à d et d' passant par M (//d et //d')
- Tracer deux perpendiculaires à d et d' passant par M formant les segments MA et MB
- Tracer deux perpendiculaires à //d et //d' passant par A et B et coupant //d en B' et //d' en B
- Tracer un parallèle à d passant par B' et une parallèle à d' passant par A'.
- Relier M à l'intersection des deux droites de (4.)
cela ne marche que si M est déjà à l'origine sur la bissectrice de d et d'.
Si on fait un dessin avec des droites différentes, et une position de M différente, cela ne marche pas.
M est forcément à l'origine de la bissectrice, parce qu'on //d et //d' sont les parallèles à d et d' passant par M.
Fait un dessin avec une position de M différente (beaucoup plus proche d'une des droites) et tu verras que cela ne marche pas.
Wep, je vois trente six seb me l'a démontré :). Je me dis qu'il doit bien y avoir une solution de tracé, pas juste avec Thales et mesure.
Un indice, je crois que ça marche avec des parallèles mais pas n'importe lesquelles...
trente six seb est-ce que ça c'est mieux ? la ligne rouge étant la solution.
Boris Beaulant Commentaire du deuxième essai. C'est bien tenté mais il faut rajouter l'étape utilisée par fab83 
Boris Beaulant ah oui, il y a une inversion, tu reportes un point sur la parallèle de l'autre droite... effectivement ça marche.
Je vérifie mais c’est peut être bien la solution par le parallélogramme...
Bien joué (mais faut être tordu  )
)
trente six seb Je vérifie mais c’est peut être bien la solution par le parallélogramme...
C'est, mais en le diminuant pour que ça rentre sur la feuille :)
C'est le "parallelogramme inaccessible de sommet M", wahou !!
Et en fait, le fait de diominuer, c'est le principe de l'Homothétie reprise par fab83.
Ha ha désolé de t'avoir empêché de dormir ^^
Il y avait des méthodes visuellement qui ressemblaient à ça.
C'est élégant ces solutions à base de parallélogramme.
Je pense que c'est toutefois peu précis, en terme de tracé, quand le parallélogramme est très écrasé (c'est à dire quand l'angle entre les deux droites d et d' est très petit). Parce que déterminer l'intersection de deux droites qui forment un angle très petit est source d'erreur...
intéressant Boris Beaulant , j'arrive pas a voir pourquoi la diagonale que tu crées est parallèle à la diagonale du parallélogramme original, mais ça a l'air de marcher... tu as une démonstration ?
En fait en dessinant autrement, je me suis rendu compte qu'avec les parallèles à d et d' passant par M, on pouvait avoir deux triangles pour lesquel il était possible de montrer que leurs angles étaient égaux, et que donc l'un est une homothétie de l'autre.
Et que donc les rapport des leurs côtés sont les mêmes.
Etant donné que leur hypothénuses sont les deux côtés du parallélogramme, en prenant le rapport des autres côté, on refait un autre parallélogramme, mais avec un facteur d'échelle ...
Je sais pas si c'est clair :)
J'avoue que je commence à m'y perdre un peu avec toutes ces solutions. On voit que certains on quand même des bons niveaux en géométrie !
J'ai pas trop le temps de faire un tracé sur logiciel.
La question n'est pas de trouver le centre de l'arc qui passe par m n'est ce pas?
Mais on a un parti des deux rayons et un point de l'arc à dessiner qui est M
Donc on s'imagine sur une épure.
Depuis le point m tracer une perpendiculaire à d -> cela donne le point A
Depuis le point m tracer une perpendiculaire à d' -> B
On obtient ainsi trois points qui sont sur l'arc A M et B
Planter un clou sur les points A et B
Construire l'outil qui va tracer l'arc avec deux planchette (règles):
Il faut quelles soient plus longes que AM ou BM
Placer la première planchette reliant AM (a gauche du clou donc des points a et M)
Puis superposer la deuxième reliant BM (toujours à gauche du clou aussi)
Il y a superposition des deux règles autour de M -> maintenant il faut les lier ensemble au chevauchement-> Deux vis
Placer le crayon sur M et faire glisser ce montage contre les deux clous en montant vers A
Puis en descendant vers B. On obtient l'arc sans utiliser de compas.
En fait, pour trouver le centre du cercle passant par M, A et B, il suffit de tracer la perpendiculaire à MA passant par le millieu de MA, et la perpendiculaire à MB passant par le milieu de MB. Les deux perpendiculaires se rejoignent au centre du centre passant par M, A et B.
Et en fait, c'est la même chose que l"homothétie 1/2 qui a été proposée par ailleurs: tracer une parallèle à d passant par la moitié de MA, et une parallèle à d', passant par la moitié de MB.
la perpendiculaire à MA passant par le milieu de MA
La médiatrice de MA tu veux dire :)
Dans ce cas, c'est exactement la solution de fab83
Donc j'ai juste, sans avoir le centre du cercle, on peu tracer l'arc.
Sauf que en fait j'ai faut car j'avais compris qu'il fallait tracer un arc de cercle par le point M.
je suis hors sujet en fait!
La solution est pour moi... vieux rouleau de papier peint comme ça tu n'as plus problème initial 
J'espère que si j'ai gagné le concours, je ne gagne pas un vieux fond de colle à papier peint...
Jusqu'à 10 m de longueur ce ne serait pas un souci si j'avais du papier en réserve... ce n'est plus le cas et ce fil me fait me rendre compte que comme un c... je n'ai pas pensé à garder un rouleau ! 
Bon, pour des angles très faibles on devrait y arriver sur un rouleau de PQ, mais il y en a qui ont tout thésaurisé 
Pour ma part je répercuterais l'angle d'arrivée des deux droites sur le bords de la feuille afin de tracer la suite des droites en dedans, comme si la feuille était pliée finalement.
Pas bête, mais si la feuille est toujours trop courte ? Tu répercutes de l'autre coté ? Jusqu'au croisement ?
Je crois que cela ne marche que dans un cas particulier. Avec M positionné différemment, cela ne marche pas
Il existe bien une méthode par pliage mais ce n'est pas celle-ci ! 
Peut être que la limite est la perte de précision à chaque renvoi d'angle. OU tout simplement ça ne marche pas, je ne sais pas.
Je dirais que ça marche. La précision en limite oui.
Je dirais que la techn De boris est la bonne mais avec l'angle formé à gauche du point M et non a droite 
Oak arf, non mas technique ne marche pas. Le parallélogramme n'a pas les 4 côtés égaux.
Oak ça c'est la bissectrice. Ca ne marche que si M est équidistant des deux droites, non ?
Boris Beaulant la j'ai placé M au pif, effectivement cela demande une triangulation si M n'est pas équidistant.
Thalès peut être.
Je tiens une discussion avec ma femme et en meme temps je tente d'apporter de l'eau au moulin. 
+1 Boris Beaulant , c'est ce que j'allais dire, si M se trouve sur la bissectrice, c'est plus facile
Oui, mais si on veut faire la coupe dans la vraie vie, sur un parquet par exemple. On peut pas le plier :(
Moi aussi, j'ai réfléchi 
Et je suis parti sur le principe de la géométrie descriptive.
Je me suis dit on voit une élévation avec 2 droites et un point qui sont sur un même plan.
Donc ça se projette sur un plan, que j'ai pris parallèle à la ligne d'horizon. On imagine qu'on met le dessin au mur quoi.
Ensuite on virtuellement changer de plan en faisant tourner le plan autour d'une verticale.
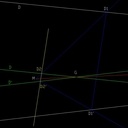
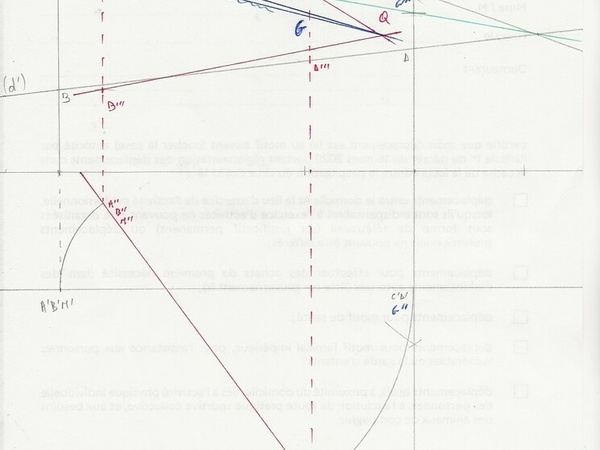
J'ai tracé une Verticale qui coupe les droites d et d' en A et B en passant par le point M.
Le bord de feuille coupe les droites d et d' en C et D.
Tout se petit monde se projette en plan sur une droite et les points A'B'et M' sont confondus, tout comme les points C'et D'.
L'axe de rotation se situe entre ces deux séries de points sur la projection en plan.
En plan, on obtient les points rouges A", B" et M" ainsi que C" et D".
En élévation, ces points se projettent en A''' B''' et M''' d'un côté puis C''' et D''' d'un autre côté.
On rejoint A''' et C''' ainsi que B''' et D''' qui sont les projections verticales des droites d et d' sur le nouveau plan.
La méthode marche, le point d'intersection des droites rentre dans la feuille. Cela nous donne... le point Q !
On rejoint M''' et Q ce qui est ce qu'on recherche. (c'est là que j'ai fait une erreur de tracé, arrivé là, je n'ai pas tout recommencé)
Cette droite coupe la verticale C''' D''' en G !
On projette le point G c ) sur le premier plan de référence.
) sur le premier plan de référence.
Ce qui nous donne le point où la droite M / intersection des droites va couper le bord de feuille.
Le compte est bon !!! 
Vous n'êtes pas autorisé à indiquer votre accord ou désaccord vos propres contributions.
L'adresse e-mail associée à votre compte doit être confirmée avant de pouvoir indiquer votre accord ou désaccord.




 .
.






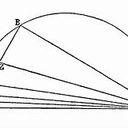
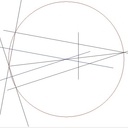
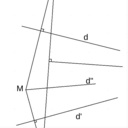
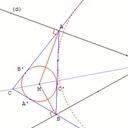







Bon, j'ai cherché une solution à base de cercles mais je n'ai pas trouvé... alors j'ai ouvert un bouquin.
Un indice,
laune solution se trouve dans:Que des cercles ?
Ce n'est pas là que je l'ai trouvée.
Il y a eu de bonnes propositions même si elles ne marchent pas. (sauf peut être celle de Kentaro).
Ce n'est pas un indice mais il y au moins 11 réponses possibles.
dneis quand le concours sera terminé, ce sera sympa de voir le domaine d'application
Je précise que les droites et le point M sont totalement aléatoire. Certaines réponses explorent même avec un point M extérieur aux droites (d) et (d').
trente six seb grrr, 11 réponses et pas en trouver un, c'est moche :(
Tu m'agaces ... hihi
Boris Beaulant finalement si, il y a en a une voire 2 de trouvées. Mais dans les 11, il y a en a des vraiment compliquées.
finalement si, il y a en a une voire 2 de trouvées. Mais dans les 11, il y a en a des vraiment compliquées.
Les plus grand noms des mathématiques ce sont amusés là dessus !
Non, la solution que j'ai lue n'utilise pas de cercles. C'était mon idée de départ qui n'as pas débouché. Je me suis mal exprimé...
L'exercice a-t-il un nom ?
Trouver une concourante à deux obliques données et passant par un point donné.
Petit malin ;)
C'est pas un nom ça, c'est une définition :P
Je me dis que si plein de gens ont cherché mille solution, il leur a bien fallu à un moment le nommer sans en faire une phrase.
Effectivement, j'ai pris bien soin de ne pas utiliser les mêmes termes que le site internet sur lequel j'avais fait cette trouvaille.
C'est "l'intersection inaccessible".
trente six seb ha oui, c'est plus facile comme ça. Y a des solutions sacrément "complexes".
Boris Beaulant oui, c'est ce qui m'a étonné à la base.
Le problème est simple à poser mais plus compliqué qu'il en a l'air.
Et on voit que la ressource en géométrie est infinie ou presque, on arrive à trouver plein de méthodes.
Sur ce site , Bricolo36 est un connaisseur Certainement qu'il appellera cet exercice avec les mots de son métier, quelque chose comme
"traçage d'un cône à sommet inaccessible"
Merci à tous pour votre participation, je ne pensais pas qu'on userait autant nos neurones sur cette question !
Voici le site sur lequel j'ai trouvé le problème et les solutions.
Sauf celle que j'ai proposé dans ma réponse.
debart.pagespe...ble.mobile.html
Le site est franchement bien, pour ceux qui n'ont pas encore mal à la tête vous pouvez aller y faire un tour.
Mais c'est moins marrant qu'ici.
Ça n'empêche pas de continuer à jouer pour ceux qui veulent.