Bonsoir à tous,
J'essaie de comprendre les rudiments de la Géométrie Descriptive et ce n'est pas toujours très simple.
Le livre des 20 leçons va bientôt arriver mais en attendant, j'ai repris la partie du Traité Complet de Menuiserie qui traite de la Géométrie.
A la deuxième lecture, certaines choses se sont éclaircies.
Mais il reste des questions insolubles.
Voici la première :
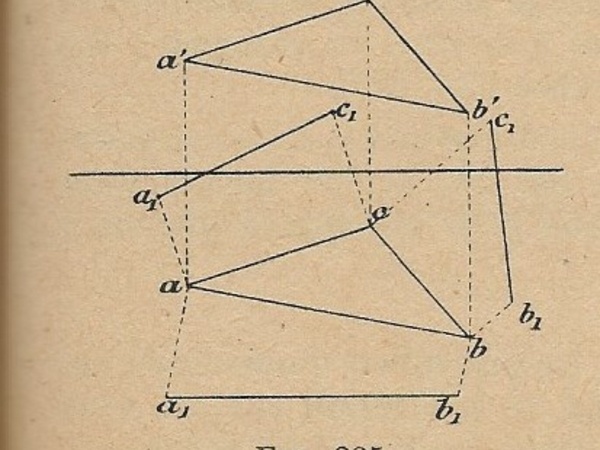
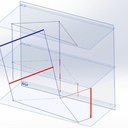
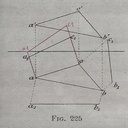
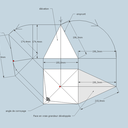
La figure 225 de la photo jointe est accompagnée de l'explication suivante : déterminer la grandeur d'un triangle connaissant les projections des 3 sommets. (voir photo 3)
Nous avons bien les triangles abc et a'b'c' formés par les projections des 3 sommets, séparés par la ligne de terre.
Les vraies grandeurs en éclaté a1c1, a1b1 et c1b1 sont construites en reportant à partir de la vue du bas (sur le sol) les hauteurs reprises sur la projection du haut (sur le mur).
Ainsi, la distance ligne de terre / b' est bien reprise pour projeter b1 à partir de b (perpendiculairement à cb d'une part et ab d'autre part).
Jusque là tout va bien et je pense avoir compris.
Par contre, la vraie grandeur du côté a1c1 m'échappe : les deux a1 et les 2 c1 ne sont pas égales distances. (j'espère être clair).
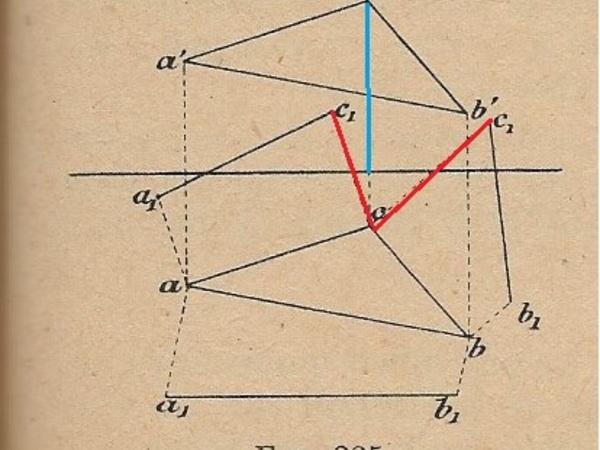
En reformulant : pourquoi est ce que les 2 lignes rouges ne sont pas égales entre elles et ne devraient elles pas êtres égales à la ligne bleue ?
(idem à partie de a)
Merci de votre aide : soit le schéma est faux, soit je n'ai pas tout compris.
(je penche pour la deuxième solution).

Cet énoncé est peu éloquent.
La partie du Chapitre III L'art du trait qui traite l géométrie dans l'espace commence à la page 111.
Cet énoncé est page 123 et la difficulté est progressive.
Pour s'y retrouver un peu plus voici les pages 121, 122 et 123 dans leur intégralité.
Mis à jour4 réponses
C'est une erreur. Pour une question de mise en page on peut placer la nouvelle ligne de terre (y1'y1) au changement de plan frontal n'importe où parallèlement au segment du plan horizontal (c'est le cas pour le segment cb où y1'y1 est collinéaire avec cb).
Dans ce problème on a trois changements de plan frontal et les distances cc1 à droite et cc1 à gauche n'ont pas besoin d'être identiques, par contre la différence entre les segments aa1 et cc1 à gauche doivent être identiques dans l'ancien et le nouveau plan frontal (distance jusqu'à la ligne de terre).
Hello perso je suis un adepte de l'immersion concrète et utile dès le départ (art du trait) !! j'ai toujours eu du mal avec les explications théoriques de ce genre .
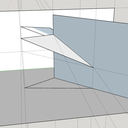
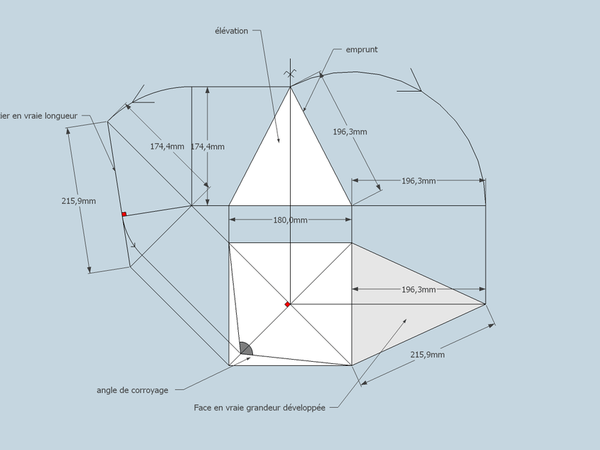
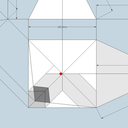
Dès que l'on m' a dit (en charpente) , pense pyramide , tout c'est éclairé d'un coup !
Le schéma ci dessous devrais illustrer mes propos !
pourrait tu nous donner l’énoncé exact de l'exercice et n'y aurait il pas en préambule de la série d'exercice des infos qui pourrait nous servir ?
ce qui me dérange c'est le "Les vraies grandeurs en éclaté" pour moi le éclaté signifie un placement aléatoire des droites a1c1 / a1b1 / c1b1 les pointillés aa1/bb1 par exemple ne sont là que pour montrer de quelle droites ils sont issus .... bref qqch m'échappe







 Mais c'est bien : je pense que j'ai compris là où je ne comprends pas.
Mais c'est bien : je pense que j'ai compris là où je ne comprends pas.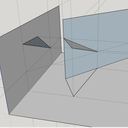







Merci à tous pour vos réponses !
Elles me permettent de mieux comprendre la Géométrie Descriptive et d'éviter un raccourci fâcheux.
En même temps j'ai compris un autre point essentiel : il est souvent question de la droite AB et celle ci n'apparait pas sur l'épure.
En fait AB est la droite "réelle" ou "en perspective" et sur l'épure n'apparaissent "que" les projections nommées avec des petits a et b : a1b1, a'b', etc...