Bonjour à tous,
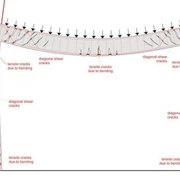
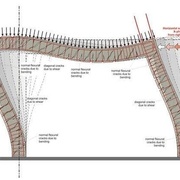
J’ai trouvé par hasard ces schémas qui montrent comment réagissent les portiques . Celui-ci est en béton armé mais peu importe s’il avait été en bois il aurait réagi de la même manière. On voit bien les fissures qui correspondent aux moments de flexion et celles qui correspondent au cisaillement. Je signale que ce calcul est extrêmement simple à effectuer c’est l’une des premières choses que l’on réalise quand on apprend la RDM (on est loin de la mécanique des milieux continus mais pour un truc aussi simple cela suffit). Alors la question que je me pose est la suivante : en bois on réalise des triangles pour réaliser des encastrements, mais quand le triangle est en traction comment est réalisé l’encastrement ? Une simple clavette qui va solutionner le problème ?
Un forumeur a déclaré un jour qu’il n’y avait pas de calcul en charpente. Cela m’a rassuré. Au moins quelqu’un qui a fait pas mal de choses et qui est conscient de les avoir réalisées « par expérience ».
Mais un autre forumeur a déclaré qu’il était capable de calculer une ferme : alors là j’ai longtemps rigolé car selon moi les fermes de charpente sont incalculables avec la théorie des poutres. Et bien entendu je ne parle pas de la théorie de l’élasticité qui n’est jamais employée en construction.
Comme quoi il y a de tout parmi les forumeurs….c’est la fameuse courbe de Gauss.
A bientôt et réfléchissez à cette clavette qui reprend tout le moment d'encastrement qui est assez considérable.
3 réponses
En fait, cela fait des dizaines de milliers d'années que les hommes font des constructions en bois, et des charpentes, et cela sans calcul. Ils ont même fait des trucs capables de supporter des contraintes dans tous les sens, même pendant un tremblement de terre, et il y a des temples japonais qui sont encore debout, même après 1000 ans de secousses permanentes... Et tout cela, sans calcul, avec essais/erreurs et retours d'expérience.
La plupart du temps, ces structures sont largement surdimensionnées, overbuilt, comme disent les zanglais, mais ça marche.
Le recours aux calculs est devenu nécessaire quand on a commencé à vouloir gagner plus de fric, et optimiser les trucs (économiser sur les coûts, sur la matière, sur la main d'oeuvre, etc).
Pour cela, il faut mettre le moins de matière possible dans la structure, et le plus possible de charges et de contraintes. Dans ce cas, les concepteurs s'amusent à être aux "limites", et pour cela, il faut des calculs de plus en plus subtils. Mais dans ce cas, en effet, il ne faut pas nom plus oublier la question de la "clavette"... C'est souvent là que les calculs pêchent...
Le capitalisme a créé les besoins en calculs.
Mais les deux approches font du sens.
Tout a fait d'accord!
J'ajoute, pour avoir manipuler et développer des modèles de calcul pendant une quinzaine d'années - sans rentrer dans les détails, cela concernait des modèles de propagation, que les résultats bruts de ces modèles accompagnaient toujours d'une correction des résultats par le fameux coefficient de sécurité...qui donnait systématiquement le même ordre de grandeur que l'abaque graphique utilisable par simple lecture avec un papier et un crayon, basé sur l'expérience et existant depuis quelques décennies.
Bonjour,
En ce qui me concerne je n’ai aucune affinité concernant les constructions réalisées « au pif » des charpentiers. J’ai lu sur ce forum des indications de gens très sérieux qui montraient comment calculer des constructions. A mon sens tout était erroné dû au manque de formation de ces gens. Je ne leur en veux pas mais c’est ainsi. Aussi ai-je été rassuré lorsqu’on m’a indiqué que les calculs n’existaient pas dans les structures des charpentiers.
Attention je ne parle que des petites structures réalisées par des charpentiers car les grosses structures en bois, celles qui passent par un BE sont correctes, mais il y a un fossé entre les deux.
Au point de vue des connaissances en calcul de structures on a fait un bond considérable en une génération. Il y a pas mal de temps lorsque j’étais étudiant en 1973 on étudiait le béton armé aux états limites (déjà l’élastoplasticité dans le béton). Aujourd’hui si l’on regarde les règles des Eurocodes pour la construction métallique on voit que celles-ci prennent en compte les non linéarités géométriques ainsi que les non linéarités dues à la loi de comportement….on est à l’infini de la RDM. Je ne sais si c’est appliqué, car pour dominer ces choses c’est loin d’être évident mais cela existe dans certains programmes de calcul.
En ce qui concerne les assemblages par triangles avec clavettes, j’étais capable (j’ai écrit à l’imparfait car aujourd’hui en retraite depuis 14 ans………) de les calculer sans aucun problème avec les théories modernes, mais je reconnais que ce n’est pas le job d’un charpentier. Il faut aussi se rappeler que la connaissance de la construction n’est pas venue en quelques jours…..que de catastrophes lorsqu’on est passé de l’art Roman à l’art Gothique, pour les constructions de voutes !!!!
Donc encore une fois je ne sais ce qui existe dans les vraies règles Eurocodes des constructions en bois, mais je suis très étonné que les charpentiers en soient encore à l’âge de pierre. Ce n’est pas une critique mais une simple contestation. Mais bon chacun fait suivant sa technique, et le monde continuera de vivre
A bientôt
Concernant ta question sur les encastrements en triangle, si je dois traduire en termes de charpente, j'imagine que ton encastrement est un tenon-mortaise, et que la clavette dont tu parles est une cheville.
Oui, cela suffit dans la plupart des situations, entre autres parce qu'un assemblage de charpente travaille rarement uniquement en traction.
En fait, dans le cas du tenon-mortaise chevillé, la partie la plus fragile de l'assemblage est le tenon puisqu'il risque, s'il y a du jeu dans la mortaise, de se fendre à l'endroit où il est traversé par la cheville et donc de n'être plus tenu par celle ci.
En général pour éviter ça on sacrifie un ingénieur en faisant des incantations au dieu cornu, comme depuis l'âge de pierre.
Bonjour
il ne faut pas oublier les constructeurs de cathédrale qui ont poussé le modèle gothique jusqu’à ses limites et l’effondrement des édifices qui en suivit…
même si les modèles mathématiques n’existaient pas encore, les maîtres d’œuvre devaient avoir en eux-mêmes les ferments d’une pré-science de la construction et des états limites de la matière ! 
Licence
Je ne suis pas charpentier mais j en ai cotoyé assez pour savoir qu un bon charpentier ne dessine pas une ferme au pif.fr.wikipedia.o...pure_de_Cremona
Je ne vois pas ce qu'est une clavette dans un assemblage bois ? C'est la cheville ??