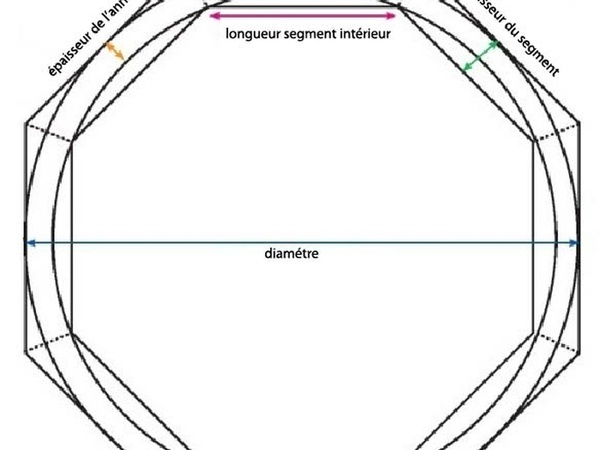
bonjour les boisseux et boisseuses , je suis à la recherche de la formule mathématique pour calculer la longueur exterieur des segments, a partir du diamètre final et du nombre de segments ( longueur du débit) je joins une pj pour mieux m'expliquer
5 réponses
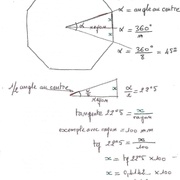
exemple pour un octogone avec 100 mm de diamètre suivant ton plan
formule pour l'angle au centre d'un polygone régulier
Juste vérifier que les unités utilisées par le tableur ou de la calculette sont les bonnes (degré ou radians, le cercle complet fait 360° ou 2 pi radians (2 x 3.1416...), donc le cas échéant convertir les mesures d'angle (1° = 2 pi radians/360).
Sinon, les calculs de type 2r × cos(α/2) provoquent des arrachements capillaires et des crises de nerfs dommageables pour le matériel et la paix des ménages 
Slt, je sais pas si c'est exactement ça que tu cherches, tu as aussi ces abaques: spacecoastwood...rning_Table.pdf , par rapport au diamètre ça te donne le nombre de morceaux et les angles, mais c'est en anglais...si ça peut t'aider.
cette page donne des billes.
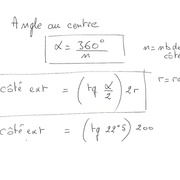
la formule serait :
Un côté mesure 2r × cos(α/2).
avec l'angle α valant 180-360/nombre de cotés du polygones
par contre le diamètre ici est celui englobant le polygone, donc de sommet à sommet. (pas du milieu de l'arête comme sur votre dessin)




un grand merci a tous je viens de faire sur exel je contrôle si mes résultats sont juste apparemment ça colle entre les calcul ,tableaux et exel à suivre @+
Bonjour les amis, j'ai un souci et j'espère que quelqu'un pourra de me venir en aide. J'ai créé un tableau sur excel et lorsque je demande la tangente d'un angle de 22.5° j'ai un résultat de 0.5578 alors que la réponce correcte est de 0.4142. Pourquoi?
Mouligneau parce la fonction tan() renvoie la tangente d'un angle exprimé en radians, il faut donc le convertir en degrés (enfin plutôt en radians) : =tan(radians(22,5)).
Ou sinon, sachant que 22,5° c'est PI/8, tu fais tan(PI/8), tu trouveras bien 0,4142.
Ara y sont chiants.... y zauraient quand même pu faire un truc simple avec des degrés...c’est vraiment pour em... l’monde...
Tout ça à cause des sumériens qui savaient pas compter autrement qu’en base 60...
Kentaro la base 60 est quand même géniale, surtout quand personne n'a encore inventé les chiffres décimaux : tu peux diviser par 2, 3, 4, 5, 6, 10, 12, 15, 20, 30... avec ça, besoin de rien d'autre !
Mais les radians, ça c'est vraiment la classe... un angle égal à une longueur, que c'est beau !