Bonjour à tous.
Ce matin, j'allais vous poser une question concernant l'un des exercices contenus dans les 20 leçons d'André Ricordeau.
Et puis finalement en rédigeant la question, j'ai trouvé une réponse, ce qui finalement n'est pas si rare.
Par contre, la méthode trouvée me convient à moitié et je pense qu'elle ne fonctionne que quand un prisme a ses arrêtes paralèlles entre elles.
Du coup, ma première question évacuée, en voici une seconde.
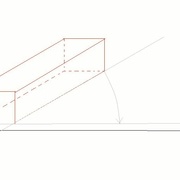
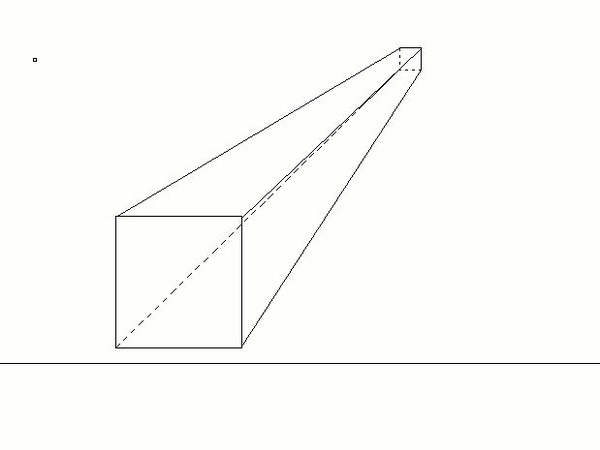
Soit un prisme dont on voit la projection frontale.
Je veux le faire tourner suivant le centre de rotation O afin de rendre les arrêtes parallèles à ligne de terre.
Pour l'arrête qui comprend O, c'est facile.
Pour l'arrête AB, il suffit avec le compas en prenant O pour centre de décrire des arcs de cercle à partir de A et B.
**
Oui, mais comment savoir quel est le point de l'arc de cercle qui convient ?
A quel moment s'arrêter dans la rotation ??
C'est cette question qui m'a turlupiné ce matin.
La réponse est simple : quand la projection de la droite AB est perpendiculaire à la ligne de terre.
Oui mais comment le tracer ?
Voici comment j'ai procédé.
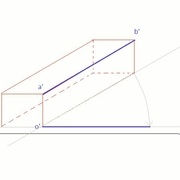
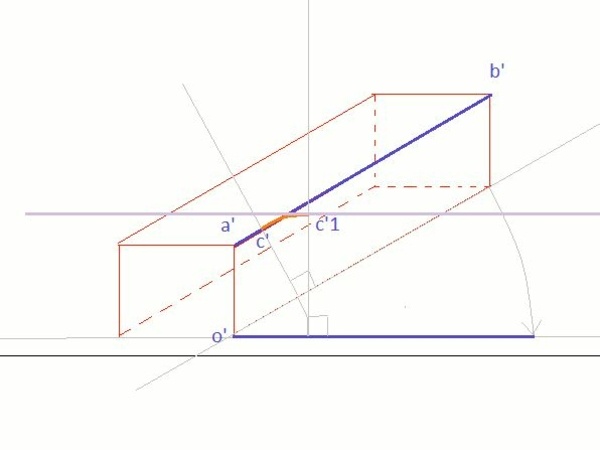
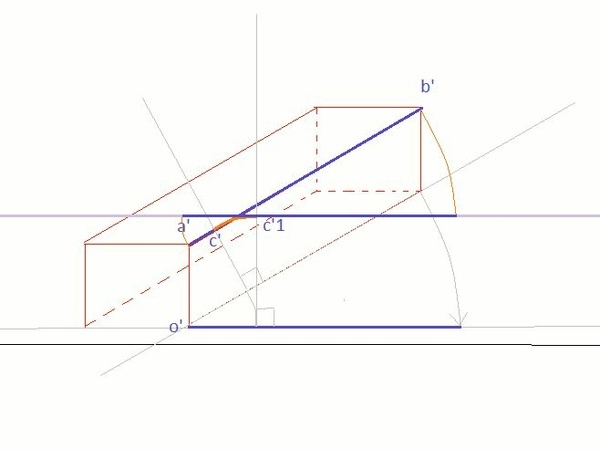
Je trace une perpendiculaire à l'arrête qui passe par O sur la projection initiale et sur celle qui a tourné.
La perpendiculaire coupe AB en C.
(c') se projette en c'1 par rotation de centre O
l'arrête AB après rotation passera donc par c'1
Les rotations des points A et B donnent les bornent de l'arrête (a'b')
Il suffit de faire la même chose pour toutes les arrêtes et de rejoindre les sommets.
Est ce que vous utilisez la même méthode ?
Je n'ai pas l'impression que ce soit le plus simple.
Et puis... comment fait on lorsque le prisme ne possède pas d'arrêtes parallèles entre elles ??
Merci de vos lumières, bonne journée à tous.
Désolé pour les dessins faits avec paint.
Mais c'est plus lisible qu'au crayon de papier sur une feuille.
Mis à jour1 réponse
Bonjour cher Collègue,
Ton approche n'est pas la meilleure.
Si tu veux traiter la géométrie descriptive depuis la base, telle qu'elle est présentée dans l'ouvrage de Ricordeau, tu as omis de tracer la deuxième vue en-dessous de la ligne de terre, qui est indispensable pour comprendre les manipulations à effectuer.
Cela n'est en rien compliqué, c'est comme avoir une vue de face et une vue de dessus, la géométrie descriptive est d'ailleurs la base du dessin industriel. Et si tu sais faire une vue rabattue, tu n'as pas besoin de développer des connaissances en géodes, à part si tu veux faire des tracés plus complexes. C'est un verbiage bien inutile pour des constructions courantes.
Il serait intéressant que tu nous donnes la totalité de l'exercice.
"Rotation d'un prisme" : non, ce n'est pas une rotation mais un rabattement et tu ne rabats pas un prisme, mais un segment pour le transférer sur le deuxième plan de vue. Voir le dessin ci-desous et suit le segment FJ.
Tu rabats un segment jusqu'à la parallèle au plan de projection représenté par la ligne de terre qui est l'intersection entre le plan de tracé et le deuxième plan perpendiculaire : frontal ou de dessous.
"Oui, mais comment savoir quel est le point de l'arc de cercle qui convient ?"
Quel point ? Le centre du cercle ?
"A quel moment s'arrêter dans la rotation ??"
Lorsque tu as rabattu le point sur une parallèle à la ligne de terre.
Oui le rabattement, j'ai compris.
C'est la rotation que je ne comprends pas.
page 39 du même livre ;-)
Ricordeau fait tourner le prisme autour d'un point.
Et à partir du prisme tourné, il projette la vue de horizontale.
Il n'y a donc pas besoin de la vue horizontale pour faire la rotation.
Principe : Cette méthode consiste à faire pivoter l'arêtier autour d'un axe vertical jusqu'à ce que les arêtes deviennent des droites frontales.
Qu'est-ce que tu ne comprends pas dans cette phrase ? Connais-tu la définition d'une droite frontale ?
La rotation de la pièce représentée (l'arêtier ici) s'effectue dans l'espace, en conséquence cette rotation est représentée sur les deux plans frontal et horizontal.
L'arêtier est un terme que je n'utilisais pas, cela doit être spécifique à la menuiserie.
Je conseille de regarder le cours de géométrie descriptive du Chevalier, le guide du dessinateur industriel (appelé gedï par les djeuns "Dgi","di", "aîe"), il est facile d'abord et bien représenté.
Un GDI est facilement trouvable ( 5€ sur leboncoin), même un exemplaire des années 80 est encore valide sur bien des points.
Un guide intéressant : Géométrie Descriptive
Si, ç ay est j'ai compris (voir un peu plus bas les explications).
J'avais compris le principe mais je n'arrivais pas à le tracer. En tout cas, pas de manière satisfaisante.
L’explication est que les écartements entre les arêtes restent constants.
Merci pour la référence, si je croise un Chevalier GDI, je ne manquerai pas de l'attraper au vol. D'ailleurs, j'en ai trouvé une version PDF qui ne me semble pas très légale, du coup je ne la partage pas en public.
L'arêtier doit même être un terme de charpente à la base.
justinstorck.f...r/a/aretier.php
(un article très intéressant)
Les // de af ch bg ont un écartement que l'on retrouve sur l'autre vue après rotation les arcs de cercle coupent ces// ce qui détermine les nouveaux points a f1 C1 H1 B1 g1 . Les écartements sont marqués / et //.
ah oui merci kaj, bien vu ! Les écartements restent constants.
Mais du coup pour le tracer, il faut mesurer ?
Ou on arrive à le faire au compas ?
kaj oui faut passer par une perpendiculaire.
C'est toujours mieux que 2 comme je proposais au début.
En tout cas, je suis content, cette leçon m'avait pas mal enquiquiné depuis le temps que j'y suis...
Je pense qu'il faut reporter au compas ou alors reporter fghe au compas en f1. En gros comme tu fais une rotation par rapport à une face du prisme, les distances sont conservées au niveau des faces et tu peux reporter la distance fh en f1 au compas et en déduire h1 par l'intersection des deux arcs de cercles
benjams ah oui, je vosi ce que tu veux dire. J'ai l'impression que c'est bon aussi. Faudra que j'essaye.
Et du coup ça résout aussi le problème des arêtes non parallèles.
Tu peux reporter une surface au compas avec la longueur des côtés et la longueur des diagonales, comme pour une prise de mesures (il faut trianguler )
Oui, c'est que je n'avais pas vu que beaucoup de choses restaient dans les mêmes dimensions. Je n'ai pas encore tous les réflexes et j'ai parfois du mal à anticiper les résultats de certaines opérations.
Faut que je bosse pour ça.
En fait, comme tu fais juste une rotation perpendiculaire à la vue de face, sur ta vue de face aucune dimension ne change
Licence
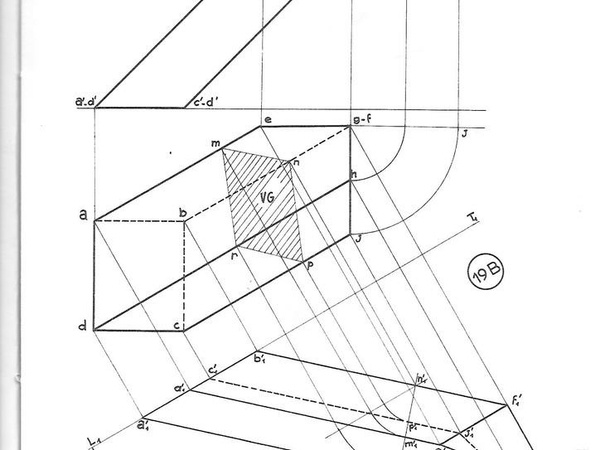
Sur Ricordeau la méthode est page 39, le centre de rotation est le point a ensuite af devient af1, tous les points ont leur centre en a. Ici les // croisent les arc décrit et la figure a fait une rotation. Si tu fait la rotation d'un pied gainé, reproduit les sections hautes et basses ensuite tu a les arêtes
Oui j'ai bien vu ça.
Je n'ai pas de souci pour "faire tourner" à partir d'un point mais jusqu'où la fait on tourner ?
trente six seb proposition d' une progression (avec un peu d’humour, il en faut...)
kaj excellent !
C'est ce livre (fr.shopping.ra...bles-Livre.html) ? Pas très cher en plus.
En son temps, j'avais publié les plans