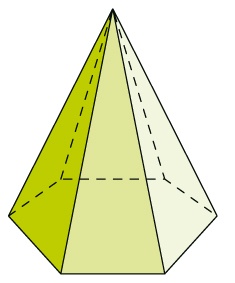
Cette feuille de calcul permet de déterminer, pour une pyramide hexagonale, inscrit dans un cercle de rayon r et de hauteur h, les angles dièdres entre chacune des faces, les pentes, et les longueurs des triangles. Cela peut être calculé pour une pyramide avec axe décalé.
Autres plans de
Kentaro



Discussions
Ce fichier est très impressionant. Je l'ai parcouru un peu, sans vraiment comprendre, mais j'ai une question :
Il me semble que la seule formule de trigono utilisée est le théorème de Pythagore, qui ne fonctionne que pour les triangles rectangles.
Or cette pyramide éventuellement désaxée n'en a aucun, à moins de découper chaque triangle en deux ?
J'ai remarqué que le fichier exécute pythagore "en 3D", c'est à dire x² + y² + z² = h². Mais comment crèe-t-il les triangles rectangles ?
Aussi, une deuxième question : serait-ce difficile de l'adapter pour des pyramides à base triangulaire, carrée, etc., toujours potentiellement désaxées ?
Nairod La racine de (X2+Y2+Z2), ce n'est pas pythagore, c'est un calcul de norme de vecteur (ou de distance entre deux points dans l'espace 3D).
Soient deux points dans l'espace, de coordonnées (X, Y, Z) et (x,y,z). La distance entre les deux points dans l'espace se calcule comme étant la racine carrée de
(X-x)^2+(Y-y)^2+(Z-z)^2
Et on peut en effet l'adapter avec des bases triangulaires, carrées, ou un hexagone irrégulier.
Kentaro Ok d'accord !
Je pense que prendre la différence des coordonnées (par exemple X - x) équivaut à prendre la longueur d'un segment de droite sur l'axe de ces coordonnées.
Idem pour les axes Y et Z, et du coup on a un parallélépipède rectangle et on peut appliquer pythagore "en 3D".
Il me semble que c'est ce que ta formule fait ?
Bon du coup je pense que je réponds à ma question du dessus : les triangles rectangles viennent probablement de ces calculs de coordonnées qui crèent des parrallelelllepipèpèdes ( ) rectangles et permettent d'appliquer Pythagore.
) rectangles et permettent d'appliquer Pythagore.
Nairod Oui, ce sont des calculs à partir des coordonnées xyz dans un repère orthonormé.
Avec du calcul vectoriel, produits vectoriels, produits scalaires, matrices, etc. C'est beaucoup plus puissant que la trigonométrie, car plus souple.
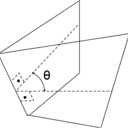
Pour calculer l'angle diedre entre deux surfaces quelconques (définies par 3 points quelconques), tu as ceci:
Si tu me donnes les dimensions de ton bureau, je peux te calculer tous les angles dièdres.
Kentaro C'est une approche vraiment intéressante. Je la garde en tête pour le jour où SketchUp me fera défaut
(c'est pas open source, ils forcent à utiliser leur version intégrée au navigateur, etc etc.
Donc je suis bloqué avec une vieille version de 2017 qui va probablement rendre l'âme d'une façon ou d'une autre bientôt).