Trisection du carré de bottcher

Salut à tous

Milles excuses pour avoir placé dans un premier temps ce document en "création" alors que sa place est ici dans les plans.

Un exemple de trisection du carré

Si comme d'habitude on me demande à quoi ça peut bien servir? Je réponds toujours: "au moins à faire plaisir à ceux qui aiment".

Cette dissection donne par exemple la possibilité de fabriquer un jeu de trois tables carrées qui s'assemblent et se transforment pour en former une seule plus grande et toujours carrée, ou encore en une petite et une moyenne à partir d'un jeu de 6 à 10 tables de formes variées à trois pieds (quelques fois quatre).

Une trisection du carré est constituée d'un jeu de pièces qui peuvent s'assembler soit en un grand carré soit en trois petits carrés dont la surface est par définition le tiers du grand carré.
On peut rechercher des trisections avec des propriétés remarquables comme avec le nombre de pièces le plus petit par exemple! Actuellement le record est de 6 pièces et il semble bien que ce soit le nombre minimum mais l'exactitude de cette affirmation n'est pas encore démontrée (un seul contre exemple démontrerai le contraire).

On sait que certains problèmes ont des solutions avec des démonstrations géométriques qui n'utilisent que la règle et le compas. Qu'il existe aussi des problèmes géométriques non solubles avec la règle et le compas comme la quadrature du cercle, la trisection d'un angle quelconque ou la duplication du volume du cube.

Il en existe plusieurs et bien que ce problème soit étudié depuis l'antiquité par des générations de mathématiciens la dernière découverte sur le sujet est assez récente et l'œuvre d'un amateur. C'est celle d'un copain Christian Blanvillain qui en 2010 a publié une solution totalement nouvelle avec seulement 6 pièces et justement une propriété particulière la surface de chaque pièce est égale!

Visitez son site qui donne les plus connues: qucub.com/home_fr
Un très joli défi géométrique sera pour vous de (re)trouver une démonstration de construction des neuf cas de trisection du carré donnés dans le site de Christian Blanvillain.

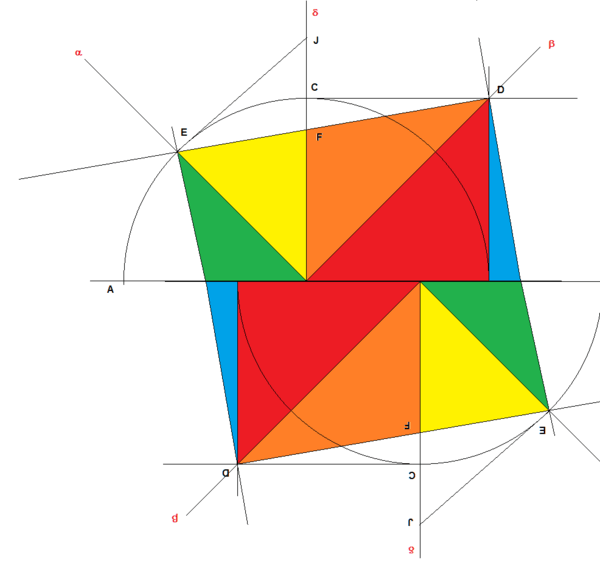
La démonstration pour celui de bottcher:
On part d'un demi-cercle de centre O et de diamètre AB=2 unités.
On trace perpendiculaire δ à AB passant par O et les bissectrices α et β des angles AOδ et BOδ
δ coupe le cercle en C
D est sommet du carré BOCD de coté unité donc sur β
α coupe le cercle en E
On trace la droite passant par ED elle croise δ en F
La perpendiculaire à ED en E coupe AO en G
La perpendiculaire à ED en D coupe AB en H
La perpendiculaire à EO en E coupe δ en J

Le triangle FCD est identique à HBD car:
CD=BD=1 et ils sont rectangles respectivement en C et B
CD est perpendiculaire à BD et FD à DH donc l'angle FDC= HDB
les angles encadrants les segments CD et BD sont respectivement égaux (CQFD).
Le triangle EGO est identique à EFJ car:
L'angle GOE fait 45° par construction et l'angle OJE a ses cotés OJ perpendiculaire à GO et EJ perpendiculaire à OE.
Le triangle OEJ est donc rectangle en E et isocèle EJO=EOJ=45° donc EO=1=EJ.
L'angle JEF et l'angle OEG car les cotés EJ perpendiculaire à EO et EF perpendiculaire à EG.
Un coté égal et deux angles égaux pour EGO et EFJ (CQFD)

1= ODB = ODC (2+5) = OJE (3+4) sont des demi-carrés coupés par la diagonale
2= OFD
3= OFE
4= OEG = JEF
5= BDH = CDF

Il est donc assez facile avec 6 demi-carrés de surface 1/2 de faire 3 carrés de 1 de surface ou 1 carré de 2 et 1 de 1 de surface. Par contre la démonstration de construction donne la solution de construction du carré de 3 qui elle est moins évidente.

le même article sur mon blog:
puzzles-et-cas...rre-de-boetcher