Dôme géodésique F3 - Goodkarma
Rayon de la sphère = 1 m → faire un facteur d'échelle pour obtenir une autre valeur de rayon.
Mise à jour : j'ai ajouté un second fichier, avec les dômes en fréquences 2 et 3, en Goodkarma mais selon 2 méthodes différentes.
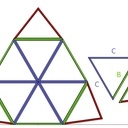
► La première avec des chevrons de section trapézoïdale, un peu plus longue à fabriquer (puisqu'il y a plus de coupes) mais avec des sommets bien propres.
► La seconde est celle que l'on retrouve dans le calculateur Acidome, avec des chevrons de section rectangulaire, plus rapide (car moins de coupes à faire) mais avec des petites différences dans les sommets (voir Img 6).




Discussions
Merci à toi pour ce plan et les différents angles, dont les angles diedres, que l'on n'a pas souvent! C'est très précieux.
(pourrais tu nous donner les longueurs des différents segments A B et C ?)
Salut Kentaro,
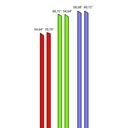
oui sans problème, voir img 4. Ce sont les valeurs pour R=1, à multiplier donc selon le rayon de notre dôme. Après je sais pas si c'est très lisible, le plus simple à mon sens est d'ouvrir le dessin sur Sketchup, faire un facteur d'échelle sur le dôme, selon le rayon qu'on veut et on aura directement les longueurs souhaitées.
Je remets les img 2 et 3 avec la précision sur la position des A et A', B et B'... sur la structure.
Bonjour, allez vous ensuite fabriquer ce dome ?
VictorDome Merci beaucoup!
Bonjour! Pour l'instant j'ai construit des dômes avec connecteurs, mais à terme j'aimerai expérimenter les dômes en Goodkarma sans connecteurs oui.
Le dernier que j'ai fait était en chêne avec des connecteurs en contreplaqué, et ça me plait bien comme ça. Mais les Goodkarma ont aussi leurs avantages.
VictorDome Merci ! En fait, je pense que c'est un peu plus compliqué que cela... Il me semble qu'il faut tenir compte de la pente au niveau de chaque "sommet". C'est un angle composé (combinaison de deux angles dans les deux sens).
Je suis d'accord. Pour l'angle de coupe de l'extrémité des chevrons B par exemple, il y a l'angle de 60,71° (comme indiqué dans img 3), mais aussi l'angle du boit de bout : 96.79° (voir img 5).
Je pense qu'on pouvoir retrouver toutes ces valeurs sur Acidome (lien fourni par Remi25 dans une autre discussion : lien)
Le plus simple pour moi est d'utiliser le plan 3D et de prendre les cotes et les angles directement dessus.
Bonjour, je ne sais pas si je peux encore poser une question au bout de 4 mois mais je tente tout de même. Je viens de me pencher sur ce type de projet et j'ai compris les différents modes d'assemblage notamment GoodKarma avec des chevrons trapézoïdaux ( qui a ma faveur).
Ma question est la suivante : comment fait-on pour calculer la section de ces chevrons dans lesquels le trapèze s'inscrit. Par avance merci.
Salut, Lyveus ,
Aucun problème pour reprendre un sujet d'il y a quelques mois.
Je vois 2 solutions à ta question : soit on utilise un calculateur comme acidome, qui nous donne toutes les infos d'angles et de cotes (voir l'image jointe pour comprendre à quoi correspondent les valeurs d'acidome), soit on le modélise en 3D (par exemple sur sketchup) et on cote pour avoir les mesures.
Re-bonjour Victordome, merci pour ta réponse.
Acidome me convient parfaitement pour faire un dôme de 1.5 m de rayon avec la méthode Goodkarma. Simplement je réitère mai question sous une autre forme: comment fait-on pour calculer la section des chevrons? La "taille des chevrons" est indiquée avec les valeurs 27 et 18 mm par défaut sans être incrémentée lorsque l'on fait varier le rayon du dôme ce qui n'est pas logique.
J'aimerais donc savoir s'il existe une formule qui corrèle le diamètre du dôme et la section des chevrons. Ou alors quelqu'un peut-il me dire quelles valeurs il a choisies pour un dôme d'environ 3 m de diamètre.
Par avance merci.
Lyveus Haa OK. Et bien à ma connaissance non il n'y a pas de formule unique pour le bois car les propriétés mécaniques sont très différentes d'une essence à une autre, selon le séchage etc... Pour d'autres matériaux on peut utiliser des abaques de charges admissibles (alu, acier...), peut-être en existe t-il par essence de bois mais je n'en ai pas connaissance (ça m'intéresserait beaucoup d'ailleurs).
Pour répondre à ta question, si ton dôme est en fréquence 2, les longueurs max font 90cm environ. D'après les constructions que j'ai déjà réalisées, je dirais qu'une section de 10cm² environ serait suffisante. Après ça dépend du bois, et de l'usage (si on suspend des choses ou pas...).
Bonjour Victor Dôme,
J'ai commencé les débits de mon dôme en respectant scrupuleusement les angles et malgré cela je ne parviens pas à assembler correctement les triangles qui ne sont pas plans . Est ce normal et si oui as tu trouvé une méthode pour que le vissage se fasse vite et bien. Au départ j'ai fixé trois carrelets sur un contre-plaqué de 12 mmm en respectant les cotes intérieures et les pentes puis j'ai bloqué mes montants avec des presses en C et vissé et ça ne fonctionne pas .
Par avance merci pour tes conseils.
Salut Lyveus. Je n'ai pas fabriqué de dôme en Goodkarma, je n'ai étudié que la conception, je ne pourrai donc pas te répondre sur la partie fabrication.
Mais la méthode de construction que tu décries me parait bonne, faire un gabarit sur un panneau et puis assembler les 3 arêtes.
Je remarque sur ton image que tu utilises la méthode Kruschke, qui permet d'avoir une base de dôme plane en F3, cela ajoute des types de longueurs différentes, dans ton exemples, on a 9 types d'arêtes différents.
Ma méthode est de dessiner en 3D sur sketchup mon modèle de dôme, et de reproduire dans l'atelier selon les cotes mesurées sur mon dessin. Si ça colle pas, comparer le dessin 3D au réel.
Bon courage pour ta fabrication!
Bonjour,
Je viens de tomber sur ce post, qui répond à une grande partie de mes questions. Merci, les explications sont au top!
Je viens de faire un petit dome/proto en good karma V2, j'ai 2/3 défauts à corriger que j'ai compris grâce à ces commentaires.
J'aimerais modéliser en 3D sur sketchup comme tu le conseils, VictorDome, mais je ne me sens pas assez caller pour le moment sur sketchup. Est-ce que tu as des tutos/ conseils à donner? Tu commencerais par modéliser les triangles à partir des cotes d'acidome et à les lier entre eux?
Merci beaucoup!
Salut Birouf, désolé je viens juste de voir ton commentaire.
Pour moi la base du dessin est le solide de base qu'on utilise, très souvent l'icosaèdre. Je n'ai pas de tuto mais je peux te dire : pour dessiner un icosaèdre, tu commences par dessiner un rectangles d'or. Ensuite copie/colle le même que tu tournes à 90° horizontalement et verticalement, et un 3ème avec encore 2 rotations à 90°. Tu devrais obtenir l'image 6 jointe. De cette figure il ne reste plus qu'à relier tous les sommets, et POUF voilà un icosaèdre, soit un solide à 12 sommets, 20 faces équilatérales.
C'est lui qu'on utilise pour la grande majorité des dômes géodésiques.
Ensuite si on divise chaque arête de cet icosaèdre en 2, on obtient un fréquence 2, en 3 un fréquence 3 etc... Quand on divise une arête, il faut toujours ramener le nouveau sommet créé à R (rayon) du centre du volume, de sorte que tous les sommets (anciens et nouveaux) soient tous à la distance R du centre.
Sinon tu peux aussi utiliser mon dessin : un facteur d'échelle pour obtenir la dimension de dôme que tu souhaites (sur le dessin R=1m). Tu peux aussi modifier les sections des arêtes du dôme en modifiant les sections des composants F3A, F3B et F3C du dessin. Quelques connaissances Sketchup sont nécessaires pour cette dernière opération.
J'espère que tu trouveras comment concevoir ce que tu souhaites!
Salut VictorDome,
Ton poste m'intéresse beaucoup car avec une partie de la sphère géodésique que je compte faire mon projet final a la fin de ma formation d'ébéniste. La question que je me pose et pourquoi tu as pris différentes section de traverse ? Est ce pour t'adapter au plus prés de la forme géodésique ? Y a-t-il un coefficient de relation entre chaque? J'aurai aimé partir avec une section de traverse de 25 mm X 50 mm même si ici, on nous apprend à travailler en pieds et pouces.
Merci d'avance pour ton retour d'info.
Aie décidément j'ai encore laissé passer un mois avant de voir le dernier commentaire, désolé Thierry.
Alors pour répondre à ta question : je n'ai pas pris différentes sections de traverse, j'ai juste expliqué la différence entre 2 techniques : soit on prend des section rectangulaire et on aura des petites différences d'arasements sur les sommets, soit on prend des sections trapézoïdales et on aura des sommet bien pointu bien propres.
Bonjour,
Merci beaucoup pour le plan c'est top. Cependant j'ai une question :
Lorsque je coupe la sphère en deux pour avoir le dome, je me retrouve avec une différence de 4 cm à certains endroit par rapport au niveau du sol.
Est ce que vous compensez cette différence avec un morceau de bois ? Ou il y a peut être une astuce que je n'ai pas compris !
Merci par avance !
Salut Chen,
Comme d'hab un mois plus tard je découvre la notification ! ;)
Oui c'est tout à fait normal, en F3 il n'y a pas d'équateur bien horizontal, donc la base n'est pas tout à fait plate.
En effet un morceau de bois permet de compenser ce petit écart (voir pièce jointe).
Depuis j'ai découvert la méthode Kruschke, qui permet d'avoir une base bien plate, avec des longueurs de bois légèrement différentes (et 4 sections différentes au lieu de 3).
Salut Victor,
Bravo pour ces avancées au niveau de la conception ; c'est vraiment enrichissant. Si je comprends bien, avec GoodKarma classique, les faces supérieures des triangles (qui constituent l'enveloppe externe) sont dans le même plan quand 2 triangles se touchent. Donc chaque face supérieure d'un même triangle est dans un plan différent. Si tel est le cas, la pose d'un éventuel contreventement (ou parement) se fait en appui sur les arêtes les plus intérieure du triangle ; toutes les arêtes extérieures étant légèrement rentrant par rapport au plan formé par l'habillage de la structure.
As tu déjà construit des zômes, et si oui, l'as tu fais en appliquant ta méthode GoodKarma améliorée ?
Merci d'avance
Nico
Salut Nico,
Oui c'est tout-à-fait ça!
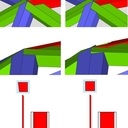
Pour dire autrement, sur l'image jointe (img 10) dans le premier cas les sections des morceaux de bois sont rectangulaires et X et X' ne sont pas tout à fait dans le même plan, de même que Y et Y', Z et Z'. Par contre X' et Y sont dans le même plan, de même que Y' et Z...
A l'inverse quand on a des sections de bois trapézoïdales, alors X et X' sont dans le même plan, de même que Y et Y', Z et Z'... et c'est plus propre pour poser des plaques ou autres sur les triangles
Bonjour Victor et merci beaucoup pour ton partage.
As-tu la formule de l'angle de coupe pour calculer le trapèze en fonction de la section du chevron (par exemple pour moi 38x60) ?
Merci beaucoup.
Salut Gugus33. Et non je n'ai pas de formule, je dessine sur sketchup et je regarde ensuite combien font les angles.
Mais sur mon dessin tu peux faire un facture d'échelle du dôme ( x le rayon de ton dôme) et ensuite tu modifies les dimensions des chevrons pour correspondre à ce que tu as.
Bonjour et merci de ta réponse rapide. Je vais me pencher dessus alors.
Super boulot en tout cas !
Bonjour VictorDome,
Bravo pour ton travail de conception. Je pense que la réalisation de ce type de dôme n'est pas facile, comme tu le précises, car les sections des brins sont trapézoïdales et les extrémités sont également suivant une découpe inclinée. En plus, plusieurs types de brins sont à concevoir selon si il construit un pentagone ou un hexagone ce qui définit différents angles de section et de découpes d'extrémité.
Bonne réalisation.
Bonjour Victor,
Super boulot le plan Sketchup en Good Karma.
Ca m' arrange bien !
Juste une question, parce que j' aime bien comprendre.
Sur le F2,l' entretoise B à l' angle dièdre côté intérieur du triangle.
J' avais jamais vu ça. Une explication ?
Ca doit être un plus galère pour l' assemblage.
Salut Lulu, merci pour ton message.
Dslé je n'ai pas compris ta question, peut-être avec un schéma?
J’ ai dis des bêtises, j’ assure pas trop avec Sketchup. Sorry.
Sinon techniquement tu maitrises un peu question étanchéité, parce que c’ est tout et n’ importe quoi les groupes FB.
Pour l’ instant je suis sur le polycarbonate et le HPL en revêtement avec un joint type pare brise, mais si je pouvais remplacer le HPL par du bois, ça ferait une saccré économie
Hello, et non désolé je ne m'y connais pas en étanchéité.
A+ !
Salut VictorDome,
Déjà bravo pour ta motivation et ton temps passé à répondre, même si je dois attendre un mois ;)
Mon projet est de construire 4 à 6 Dômes permettant d'installer un couchage double par dôme + 1 dôme bien plus grand pour recevoir séminaires et autre formations en Thérapie, Dev Personnel et Bien être ... tout ça à la campagne dans le Périgord.
La fabrication commencera fin 2025, début 2026 car j'ai pas mal d'étapes préparatoires.
Le temps étant plutôt utile pour réaliser tous les plans, devis et sélection du bois.
A aujourd'hui, je commence ma réflexion et je n'en suis qu'au début, à l'étape où je découvre et je vais me faire un premier test petit format en GoodKarma, car comme son nom l'indique, vue de loin c'est celui qui est le plus apaisant et surtout Fullbois et certainement le plus solide excepté si je méprends.
Mon intro étant faite, voici les questions que je me pose et pour lesquelle tu as peut être quelques réponses ou approches de réponses.
1/ Le site acidome.com actuel implique 3 coupes. La version actuelle de ce site corrige t'elle la propreté du résultat dont tu parles et pour laquelle tu préconises des découpes en trapèze (Image 1) ? Car il y a 3 coupes proposés par Acidome, dont la première permet d'obtenir 1 trapèze.
2/ dans l'image 2 où on voit les 3 coupes (apparemment issues de acidome), on voit l'angle "e", mais l'image de la coupe en suivant ne semble pas correspondre à la bonne arrête ? Alors que l'angle "a" lui semble être au bon endroit. Il y a certainement quelque chose que je comprends pas. Du coup, je ne suis pas certain du l'arête de laquelle je dois partir pour réaliser cette première découpe.
3/ Je suis étonné d'un sujet. On parle d'angles et de longueurs de montant dans ces discussions mais jamais au regard des largeurs et épaisseurs sélectionnées. N'y a t'il pas des implications à ces 2 choix ?
Voilà grosso modo les questions que je me pose pour réaliser ce premier test en tasseau de 24 sur 29. D'ailleurs, y a t'il une préco ? Epaisseur > largeur ou inverse ?
Salut Steph,
Wow super projet!
Question 1/ : alors sur le site Acidome, la construction des dômes se fait avec des chevrons rectangulaires, et non trapézoïdaux. On peut le vérifier en téléchargeant le fichier .obj (en haut à droite de la page du site) et en l'important dans Sketchup (il faut une extension "OBJ importer").
Mais ils indiquent quand même la valeur de l'angle e si jamais on souhaite faire la coupe pour avoir des chevrons trapézoïdaux j'imagine.
Question 2/ : effectivement l'indication de l'angle e n'est apparemment pas du bon côté. Il y a peut-être quelque chose qui m'échappe, mais en dessinant la 3D tu verras qu'il n'y a pas de confusion possible, c'est le côté qui est en contact avec le triangle voisin.
Question 3/ : oui bien-sûr, plus la longueur de ton chevron est grande, plus la section doit l'être aussi. Mais il n'y a pas de règles générales étant donné que cela dépend énormément de l'essence du bois, de ses défauts, de son séchage, de ses caractéristiques quoi, et puis de l'utilisation de ton dôme (si tu y accroches des objets, des hamacs... ou pas). Enfin si, il peut y avoir des règles générales, sous forme de de tableaux d’abaques en résistance des matériaux par exemple, mais j'en sais pas plus.
Le petit dôme que tu vas faire, c'est quel diamètre? Et en fréquence 3?
VictorDome
Merci pour ta réponse précédente qui m'a permis de comprendre que pas mal de question était encore ouverte concernant Acidome. Il fallait que je trouve les réponses de mon côté du coup :).
Pour te répondre, il s'agira d'une maquette de .425 de rayon pour commencer en V3 en largeur 38 épaisseur 27.
Je viens d'acheter le bois à Point P : 40 m linéaire pour un prix défiant toute concurrence je trouve : 25 €
Concernant les plans, je pense avoir corriger ma compréhension des différents plans et interprétations des internautes.
J'obtiens ce triangle test que j'ai lazuré pour le côté symbolique du passage d'étape :)
Maintenant, je vais passer à la phase pratique de la fabrication de ma maquette.
Et en parallèle je vais continuer sur l'identification théorique de ce que devra être la meilleure isolation : air et eau.
Bonjour VictorDome
Je déterre un peu le sujet car je potasse depuis un moment la construction d'un dome F3 pour une serre et je suis ravi de tomber sur toutes ces explications. Merci
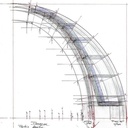
Toutefois, une question me chagrine: les angles indiqués sur ACIDOME et les angles mesurés sur les plans Sktechup (version ACIDOME ou même ta version avec les chevrons trapézoïdaux) ne corresponde pas du tout.
Ci-joint une illustration des différences sur l'exemple du montant A (en haut l'extrait du ACIDOME, en bas les cotes que j'ai tiré du plans SketchUp). Même les dimensions sont différentes (pour un rayon de 80cm).Je me trompe peut-être quelques part....
J'ai réalisé quelques premier triangle pour tester (aux dimensions et angles du plans SketchUp) et ne cela semble pas trop mal avec les côtes et angles indiqués tiré du plan sketchup.
Peux tu m'éclairer sur le sujet ? Quelqu'un a t'il déjà constaté ces différences ?
Merci
Salut sebb85,
Alors c'est un problème qui revenait régulièrement à l'époque, comprendre à quoi correspondent les valeurs indiquées sur Acidome. Beaucoup de gens se posaient des questions. J'avais fait un schéma pour faire le lien entre les valeurs indiquées dans Acidome et les angles sur une vue 3D.
Je t'avoue que ça fait un bon moment que je n'y suis plus retourné. Et en fait mon plan Sketchup m'allait très bien, alors je n'utilisais plus Acidome.
La seule chose que je puisse te dire aujourd'hui, c'est que si tu as bien dessiné ta 3D sur Sktechup, il n'y a pas de raisons que ça ne fonctionne pas dans la réalité. Jpeux pas plus.
Bonne construction!
Victor
Merci VictorDome pour ta réponse. .
.
Effectivement en partant du plan SketchUp mes essais ont très bien fonctionné. Merci
Mais je voulais m'intéresse au modèle "f3 7/12 Kruschke" pour sa base plate. En cherchant les angles sur Acidome ça a été compliqué. J'ai réussi à réunir tous les valeurs en recoupant avec les vidéos de la chaine "domo KupulArt".
Le résultat est plutôt bien sur ma maquette 1/5 ci-jointe, par contre il a un triangle de plus à faire (x35 exemplaire !).
Bonne journée
Waow, super ta maquette! Oui la méthode kruschke est vraiment meilleure. Je viens d'ajouter un fichier sketchup avec la 3D pour le F3 kruschke.
En F3 classique tu as 30 triangles AAB et 75 CCB,
En F3 kruschke tu as 30 triangles AAB, 35 CCB et 40 CCD. Donc en effet un type de triangle en plus mais ça vaut le coup.
J'espère que le fichier te sera utile
Bonne journée
Super, Merci VictorDome pour le fichier, il me sera utile
Je posterais la photo une fois ma serre achevée.
Bonne journée