Ce pas à pas présente un projet en cours de réalisation.
Le cahier d’atelier, devrait être dans le tiroir de tout établis, prêt à être consulté ou notifié !! 
C'est un outil à part entière, car il permet en temps réel d'avoir accès à tout les tracés géométriques et règles élémentaires de calculs utiles spécifiquement a nos professions, que l'on connais, mais que l'on doit parfois se remémorer en situation (ex tracé du pentagone) pour tracer une épure ou un croquis pratique dans la fabrication d'un ouvrage ou d'un montage d'usinage et de gabarits.
A mon époque en apprentissage, il s'agissait d'un grand cahier A4 moitié pages petits carreaux et page blanche en vis a vis, que l'on remplissait au gré des cours de géométrie, et in situ à l'établi pour noter certains tours de mains singuliers ( ex: cotes d'un montage de toupillage) , le tout permettant de gagner du temps .
Mon prof disait "Le carré, le cercle et le triangle sont les trois figures primaires à connaitre parfaitement pour faire de la géométrie appliquée dans nos dessins et tracés de projets complexes!
C'est comme les trois couleurs primaires qui ont donnés les bases de chefs d'oeuvre de la peinture, ou les 12 notes de musique 7 + les fameuses touches noires qui ont donné les bases des plus grands opéras!
Ici je vais essayer d’être complet, mais sans rentrer dans un ouvrage académique que l'on referme "ad vitam æternam" car peu digeste .
Mais de façon ludique donnant matière à réflexions constructives !
ici des fondamentaux intéressants, pense bête de bases d'ébénisterie : passion.bois.f...terie_index.htm
Liste des articles
- Les 3 nombres clefs des menuisiers et autres métiers faisant appel à la géométrie
- Le carré et les rectangles
- Le cercle et le disque
- Le triangle, triangulation
- Rappel : L' art du trait ! Dessins, plans, épures ....
- Les polygones réguliers utiles dans nos épures : Introduction
- Les polygones réguliers utiles dans nos épures (suite).
- Ellipses, ovales, oves et anses de paniers, utiles dans nos épures
- Tracés de divisions !
Les 3 nombres clefs des menuisiers et autres métiers faisant appel à la géométrie
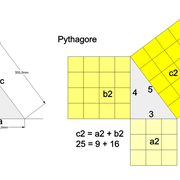
Le théorème de Pythagore (3-4-5)
Le théorème de Pythagore en géométrie, met en relation les longueurs des côtés dans un triangle rectangle. Il se défini sous la forme suivante :
Si un triangle est rectangle, le carré de la longueur de l’hypoténuse (ou côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés.
3-4-5 (ou ses multiples, ex: 90 cm-120 cm-150 cm) est utilisé systématiquement pour poser les bases des épures en charpentes échelle 1, et un menuisier doit savoir le faire pour certains chantiers sans instruments assez grand (équerre): ex implantation de parquet Versailles
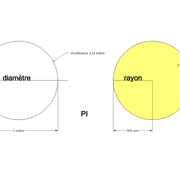
PI 3.14
π (pi), appelé parfois constante Archimède, est un nombre représenté par la lettre grecque du même nom en minuscule (π).
C’est le rapport constant entre la circonférence d’un cercle et son diamètre .
On peut également le définir comme le rapport de l'aire de surface d'un disque au carré de son rayon.
Circonférence d'un cercle = 3.14 x diamètre ; surface du disque = 3.14 x (rayon x rayon)
En menuiserie, il est utilisé très souvent !
PHI (nombre d'or) 1.618
Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b), ce qui s'écrit : (a+b)/a = a/b (1.618+1)/1.618 = 1,618
Le nombre d'or, doit être utilisé le plus souvent possible dans les études des projets à réaliser.
Ici pour comprendre la fabrication de notre compas de proportions avec PHI 1.618 .
Ici pour approfondir :
ici pour appliquer :
Le carré et les rectangles
Le carré et le rectangle, sont les formes géométriques les plus utilisées dans nos professions!
En géométrie plane, ce sont des "polygones" traçables avec le compas et la règle !
La base du tracé d'épure pour le carré ou le rectangles, commence toujours par savoir tracer une perpendiculaire à une ligne de niveau !
Le carré
En géométrie un carré est un quadrilatère à quatre côtés de même longueur avec quatre angles droits a ses sommets (90°) et deux diagonales avec intersection à angle droit (90°) . C’est donc un polygone régulier, qui est à la fois un losange si ses diagonales sont en verticale et horizontale.
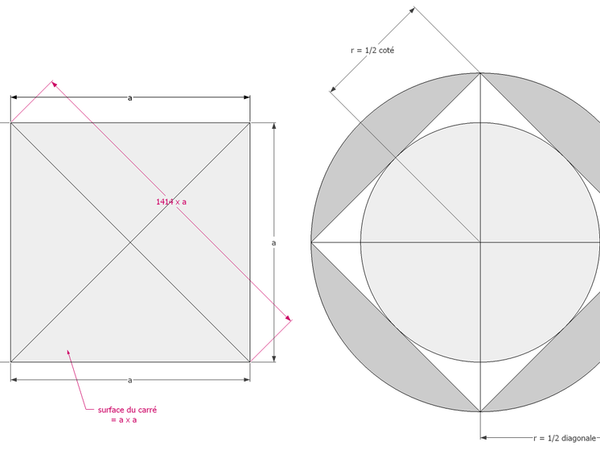
Le calcul de sa surface = longueur du coté x longueur du coté
Le périmètre = longueur du coté x 4
Longueur trigonométrique de ses diagonales = longueur du coté x 1.414
Longueur trigonométrique du coté = diagonale x 0.707
Deux cotés d'un carré et sa diagonale (45°) donne un triangle dit "demi-carré" !
Un carré peut être inscrit dans un cercle, ou contenir un cercle inscrit , en prenant le centre de ses diagonales !
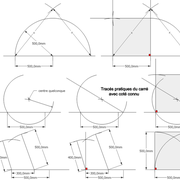
Tracé du carré depuis un coté connu
Le principe est :
1/ De tracer une perpendiculaire !
2/ Au compas de reporter les points!
3/tracer tous les cotés depuis les intersections de la construction !
Trois solutions ci dessous !
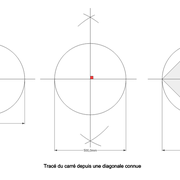
Tracé du carré depuis une diagonale connue
1/ tracer le segment de diagonale connu !
2/ tracer une perpendiculaire au segment !
3/ Depuis le centre de la construction, tracer un cercle de rayon demi segment de diagonale !
4/ Aux intersections cercle et diagonales, tracer les cotés du carré !
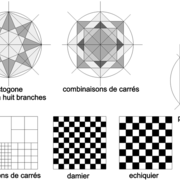
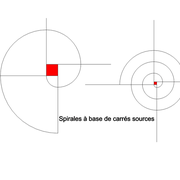
Les combinaisons de tracés et de projets en partant d'un simple carré sont infinies, quelques exemples ci dessous !
Les rectangles
Un rectangle est un quadrilatère en géométrie plane, qui est constitué de quatre sommets à angle droit 90° et de quatre côtés, reliant ces sommets deux par deux de manière à délimiter une circonférence.
Le rectangle comporte deux diagonales identiques donnant son centre ,mais deux angles différents à l'intersection .
Le calcul de sa surface = longueur du grand coté x longueur du petit coté
Le périmètre = (longueur du petit coté + longueur grand coté) x 2
Il y a quatre sortes de rectangles :
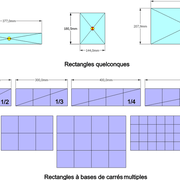
1/ Le rectangle quelconque ! aucune proportion particulière .
2/ Les rectangles double carré, triple carrés, etc. Proportions à base de carrés successifs . Ces derniers, sont utiles pour avoir des pentes de queues d’arondes par exemple, sachant que cela va de 1/6 à 1/8 !
D'autre part, un rectangle fait de N carrés, est pratique pour faire des découpes géométriques réciproques, (pour des décorations de mobilier art and craft par exemple) lairdubois.fr/...rafts-1860-1910
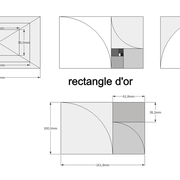
3/ Le rectangle d'or ! Tracé avec Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) , soit:
Le petit coté x 1.618 = grand coté
Le grand coté / 1.618 = petit coté
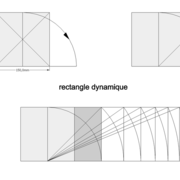
4/ Le rectangle dynamique (depuis un carré) ! La symétrie dynamique est un système de proportion.
Les deux derniers, étant utilisés pour dimensionner harmonieusement des travaux ! ici pour aprofondir :
lairdubois.fr/...e-et-nombre-dor
Quelques rectangles en usage normalisés:
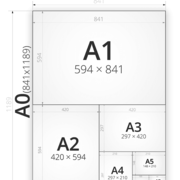
1/ Les formats rectangulaires de dessins, appelés A0, A1, A2, A3, A4, A5, A6 , Ils passent tous en formats standards inférieurs en les pliant simplement en deux , ex A1 = 2 x A2 , A2 = 2 x A3 etc.
2/ Le dessin en perspective , le point de fuite central est situé à l'intersection des deux diagonales d'un rectangle de proportion 4/3 !
3/ Les écrans de télévisions, sont des rectangles standards calculés pour le confort des images, les premiers étaient de format 4/3 comme pour le dessin en perspective !
4/ Les formats de portes intérieurs standardisées !
5/ Les formats de panneaux dérivés, (CP, medium, agglomérés, etc .) Cotes les plus utilisées :
2,500 x 1,220 et 3,100 x 1,530 mètres .
Le cercle et le disque
En géométrie, un cercle est une courbe plane fermée constituée de points situés à égale distance d'un point nommé centre. Cette distance est appelée rayon du cercle.
Parfois pour plus de compréhension, on considère qu'un cercle est un polygone régulier, formé de 360 cotés avec un angle de 360°
Quand cette figure est considérée avec une surface, sa dénomination est un disque !
En menuiserie et autres métiers faisant appel à la géométrie appliquée, le cercle et portions de cercles, sont la base de tous les tracés d’épures et de la majorité des constructions géométriques planes utiles, que ce soient pour des courbes, ou des points !
Puis des rabattements et tracés de points dans l'espace 3D dans "l'art du trait" (géométrie descriptive)
Le tout ce trace avec le symbolique et incontournable compas ! (traditionnel, ou "à verge" pour des grandes longueurs de rayons .
1/ les rapports généraux 3.14 : diamètre, rayon, circonférence, surface (voir chapitre nombres clefs).
Une polémique existe entre historiens/archéologues académiques  , et praticiens de la géométrie (nous)
, et praticiens de la géométrie (nous) , le fait que les égyptiens de l'antiquité connaissaient le nombre PI et le mètre ???
, le fait que les égyptiens de l'antiquité connaissaient le nombre PI et le mètre ???
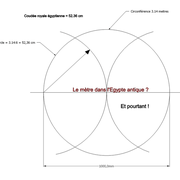
En effet, la coudée royale égyptienne a été calculée à 52.36 cm !
Si l'on multiplie cette coudée par 6, on obtient 3.14 mètres !
3.14 mètres dans une circonférence de cercle, on obtient un diamètre de 1 mètre ! Étonnant non ? 
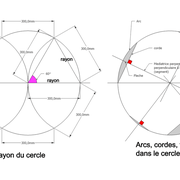
2/ Le rayon du cercle : = au diamètre :2 .
En deux coups de compas, il a la particularité de diviser en 6 parties égales la circonférence d'un cercle, et chaque points obtenus reliés donneront un hexagone (nous y reviendrons plus tard) et angles connus 60° ainsi que ses multiples .
Extrêmement utiles dans nos dessins d'études et des épures !
3/ Arcs, cordes, flèches et médiatrices : Un arc de cercle est construit par un segment de droite appelé corde, la hauteur médiane (médiatrice) entre le sommet de l'arc et la corde se nomme flèche !
En prolongeant la flèche, on obtient un rayon passant obligatoirement par le centre du cercle .
4/ Les secteurs circulaires : Issus des arcs de cercles en y traçant deux rayons depuis les intersections de la corde (portion de tarte à l'école primaire  ) .
) .
Je vous épargne les calculs trigonométriques ou Pythagore de rapport entre les longueurs d'arc, corde, flèche, hauteur , trouvés généralement par tracés d'épure pratique en atelier ! Mais je vous rappelle les calculs de bases des secteurs circulaires !
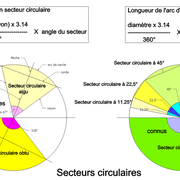
Surface d'un secteur circulaire = ((rayon2 x 3.14) : 360°) X angle du secteur circulaire
Longueur de l'arc d'un secteur circulaire = ((Diamètre x 3.14) : 360°) X angle du secteur circulaire
ex: pour cercle de diamètre 80 cm et secteur de 53°
surface = ((40 cm2 x 3.14) : 360°) x 53° = (1600 x 3.14) : 360° x 53° = (5024 : 360°) x 53° = 13.9555 x 53° = 739.64 cm2
longueur de l'arc = (80 x 3.14) : 360°) x 53° = (251,2 : 360°) x 53° = 0,6977 x 53° = 36,97 cm
Au final, nous comprenons que les secteurs circulaires, nous permettent de construire par tracés des angles facilement depuis ceux déjà connus en les divisant ou en les multipliant, puis en les additionnant (ex 90° = 2 x 45° ou 60° = 2 x 30°, 90° + 45° = 135°, 60° + 30° = 90° , etc .).
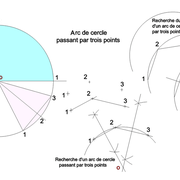
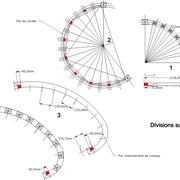
Principe de l'arc de cercle par trois points:
Dans nos dessins ou épures, il faut souvent retrouver le centre d'un arc de cercle, afin de tracer précisément ou encore pouvoir centrer un montage axé de machine pour calibrer des pièces de bois ou gabarits !(ex défonceuse)
Souvent, le cahier des charges de notre projet nous donnes directement diamètre et autres rayons, mais parfois ces informations sont inconnues, ou alors le gabarit tracé sur le chantier n'est pas propre !
Pour retrouver un centre d'arc de cercle, on applique le principe par trois points ! Sachant déjà qu'une médiatrice de corde passe automatiquement par le centre du cercle dont elle est issue.
Par les constructions ci dessous (image 1) , nous découvrons qu'il est possible de retrouver le centre d'un arc de cercle connu , ou de faire passer un arc de cercle par trois points connus ! 
Les différents arc de cercles utiles dans nos travaux en bois:
Les arcs de cercles le plus utilisés depuis l'antiquité, sont : le plein cintre et l'arc surbaissé ! Ensuite, nous pouvons construire sans limite d'autres types.
ici aussi dans les arcs utiles en architecture , les centres sont souvent à rechercher pour fabriquer une menuiserie bien calibrée ! ex ci dessous !
à suivre, les triangles
Le triangle, triangulation
En géométrie plane, un triangle est un polygone plane formée par trois points (appelés sommets) et par les trois segments qui les relient (côtés) et trois angles (somme des trois angles, dans tous les cas 180°).
En menuiserie ou autres professions utilisant la géométrie appliquée, il y a cinq types de triangles utiles que l'on étudie !
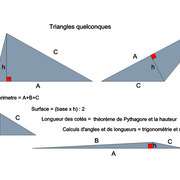
1/ Le triangle quelconque: C'est un triangle qui n'a pas de propriétés particulière !
En apprentissage, on apprend a y appliquer tous les moyens mathématiques de calculs d'angles, de longueur etc ..à condition d'y tracer la hauteur perpendiculairement depuis la base . En atelier, nous nous contentons de calculer son aire, le reste étant tracé aux instruments, puis mesuré.
En atelier, nous nous contentons de calculer son aire, le reste étant tracé aux instruments, puis mesuré.
Sur le chantier, il nous sert souvent à trianguler des prises de cotes et angles non réguliers .
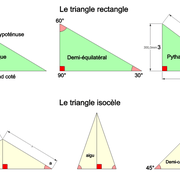
2/ Le triangle rectangle: C'est un triangle comportant un angle droit , donc chaque fois sa hauteur est à 90° (petit coté ou grand coté). Il satisfait alors le théorème de Pythagore.
Il est formé d'un petit coté d’équerre à un grand coté, les deux reliés par son hypoténuse biaise.
(Le demi-carré, est considéré faisant partie des triangles rectangles.)
Le rapport "3-4-5" (Pythagore), nous sert souvent à tracer au compas des perpendiculaires sur épures en atelier .
3/ Le triangle isocèle: C'est un triangle ayant au moins deux côtés égaux, et deux angles égaux.
En atelier Il sert aussi souvent a élever des perpendiculaires sur épures!
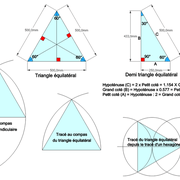
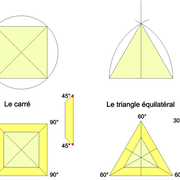
4/ Le triangle équilatéral: C'est un triangle dont les trois côtés ont la même longueur. Ses trois angles ont alors la même mesure qui vaut donc 60° et il admet trois axes de symétrie identiques (hauteurs).
En menuiserie ou autre, c'est le plus utilisé à cause de sa régularité et son tracé extrêmement facile et précis au compas, qui nous sert aussi très souvent pour élever une perpendiculaire sur épure .
Le demi triangle équilatéral (triangle rectangle) en est issu depuis sa hauteur comme coté ! (équerre de dessin 90°-60°-30°)
Ici en apprentissage, on apprend par cœur ses valeurs trigonométriques :
Hypoténuse = 2 x Petit coté = 1.154 X Grand coté
Grand coté = Hypoténuse x 0.577 = Petit coté x 1.732
Petit coté = Hypoténuse : 2 = Grand coté x 0.866
5/ Le triangle demi-carré: Voir chapitre du carré ! Il fait partie des triangles isocèles et rectangles.
En menuiserie, c'est surtout une équerre dite: "pièce carrée" (90° et 2 x 45°)!
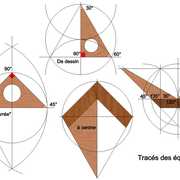
Tracés de équerres : En apprentissage, après avoir étudiés les précédents chapitres, nous apprenions à tracer les équerres, afin de les comprendre géométriquement !
Evidemment elles sont aujourd'hui largement remplacées par les équerres contemporaines, beaucoup plus précises et stables !
Triangulations
Dans nos langages professionnels, la triangulation est devenue un terme commun employé dans la majorité des projets de fabrications, prises de cotes, solidité, indéformabilité, débit économe, contrôles, etc .
Nous allons essayer de déterminer ce qui pourrait nous être utile !
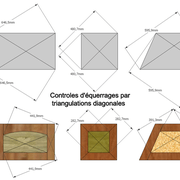
Triangulations par diagonales (vérifications d'équerrages) :
Le principe est connu depuis l'antiquité, il suffit de vérifier la mesure des deux diagonales d'un parallélogramme régulier (rectangle, carré, trapèze) , pour être certain d’être d’équerre dans une construction .
Dans l'implantation de grandes surface, c'est plus précis qu'une équerre ! (Charpente, maçonneries, etc)
Dans des ouvrages classiques, il suffit de déplacer un peu les appuis de serrages (serre joint, sangles, dormants, cale de cadreuse , etc) afin de rectifier l'équerrage désiré ! (sur le schéma, la position est exagérée pour la technique)(fig 5)
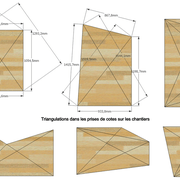
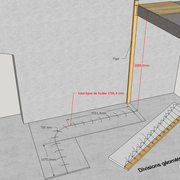
Triangulations dans les prises de cotes sur les chantiers:
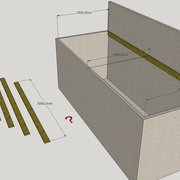
Quand parfois sur certains chantiers, nous aurions besoin de tracer le plan d'une pièce d'habitation irrégulière, nous optons pour la triangulation des mesures, afin de pouvoir replacer les points au compas et reproduire ainsi leurs géométries singulières!
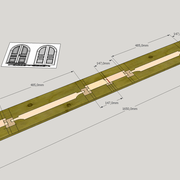
Il suffit de prendre les mesures au sol de toutes les parois, et toutes les mesures possibles depuis chaque angle ! (fig 1 , les cotes sont en mm désolé, mais le principe reste le même en mètres ! )
)
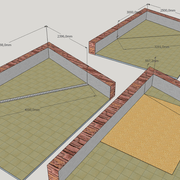
Pour relever des "grand angles" échelle 1 d'épures, pour construire des éléments dans ces angles de murs irréguliers (cuisine, bibliothèque, salle de bain etc.), on triangule avec une règle, par mesures, ou un gabarit tabletté . (fig 2)
trianguler des débits de bois :
Au prix ou l'on trouve le bois , il faut faire marcher ses neurones pour gagner en matière ! Donc économiser un peu de sous ! (y a pas de petites économies) 
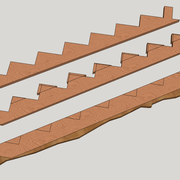
Pour des crémaillères d'escalier, on peu prendre redans dans redans, ou encore en "écoinçons" partiels.
Pour assembler des travaux circulaires, il faut partir des bois assemblés des polygones de base , puis en tirer un gabarit afin de prendre coupe dans coupe .
On peut aussi débiter en fonction du gabarit de calibrage a la toupie .
Les coupes triangulées, nous permettent d'utiliser des bois trop courts ( ex ci dessous sur des solivettes)
Trianguler des travaux afin de les rendre indéformables et stables:
De tout temps, l'homme a cherché a renforcer ses travaux en bois, il y est parvenu par la triangulation!
En effet un triangle est considéré comme indéformable grâce à ses seuls trois points reliés, qui se contrebalancent mutuellement !
Trianguler en charpente :
Trianguler est le maître mot ! La triangulation bien faite et bien assemblée sur des bois d'une charpente est le gage de sécurité et de pérennité dans le temps .
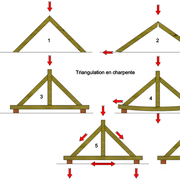
La logique de base d'un toit est un triangle formé de deux pièces de bois (arbalétriers, chevrons) organisant deux pentes reliées au sommet (faîtage).
Si ces deux bois, ne sont pas reliés à leur base, par pression sur le sommet ces deux pièces vont s’affaisser tout en s'écartant l'une de l'autre au "sol" !
Imaginons qu'elles se trouves placées sur des murs, ceux ci vont eux aussi s'écarter, engendrant ainsi l'effondrement du bâtit ! (fig 1-2)
Donc en charpente, on ajoute un bois de liaison au pied nommé entrait, et un bois vertical appelé poinçon !
Mais ceci ne suffit pas si cette triangulation effectuée n'est pas assemblée dans les règles de l'art 
A savoir que de simples coupes clouées ou vissées, vont à la longue travailler en glissement et causer à termes des désordres plus ou moins graves dans des projets d’ampleurs !
La règle générale ici c'est : "En charpente seuls les bois doivent travailler en appuis !" Les clous, vis, boulons, chevilles ect, ne sont que des liaisons et ne doivent pas travailler aux cisaillement !
Dans l'absolu, on doit pouvoir enlever toutes les liaisons sur une charpente mise en charge, sans que celle ci bouge ou se désassemble (couverture).
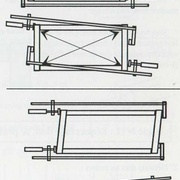
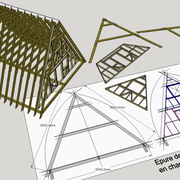
Faite l'expérience avec quelques morceaux de chevrons avec coupes clouées et une autre juste des coupes de désabouts, mise en pression par un serre joint comme sur les figures 3-4-5 ci dessous !
En résumé, la figure 6 représente une ferme "indéformable" dans les conditions normalisées.
Triangulations des tréteaux :
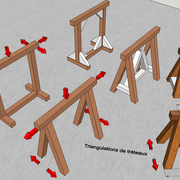
Un tréteau dans nos métiers est un outil servant a énormément de choses, pour cela il doit pouvoir porter des lourdes charges tout en étant fiable et solide!
En effet un tréteau non triangulé, peut se déformer et s'écrouler sous un poids, occasionnant des dégâts sur nos ouvrages, et pire des accidents graves sur nos personnes (chutes, écrasements, fractures et pire ! )
)
Ci dessous quelques dessins pour se familiariser avec la logique quand on construit nous même des tréteaux !
Le "must" restant le tréteau en arêtier considéré comme indéformable dut à sa forme pyramidale, qui et utilisé souvent en charpente et taille de pierre !
Leurs résistances est en tonnes .
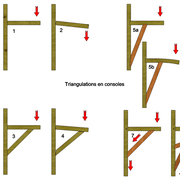
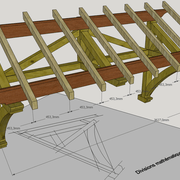
Triangulations en consoles :
Appelées le plus souvent jambes de forces ou bras de forces, ce sont des bois assemblés en biais pour trianguler les deux bois perpendiculaire d'une console .
Ici aussi, En charpente la solidité du procédé est basé sur l’assemblage correct de l'ensemble !
En travaux plus menus, cela n’empêche pas la réflexion en fonction de la charge d'une console, à savoir que ce ne sont pas des clous ou des vis qui doivent travailler ! (assemblages tenons mortaises, pigeons, dominos, lamello collés , etc .) (figs 1-2-3-4)
La position la plus efficace est de poser une jambe de force le plus proche possible de 45°!(fig 7)
Un angle trop fort de la jambe de force, apporte beaucoup de résistance, mais raccourci la portée du support ! (figs 5)
Un angle trop faible de la jambe de force, fera levier et arrachera l’assemblage tout en s'affaissant! (figs 6)
Mais parfois il faut réfléchir pour garder du passage quand une jambe à 45° empiète dans un couloir par
exemple ! dans ce cas là, on mixes les angles !(fig 8)
Cela dirige les charges au sol, en plus de faire un mouvement en "tenaille" qui à tendance à plaquer les assemblages !
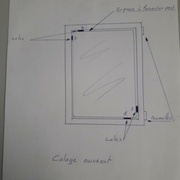
Triangulations par écharpes :
Ici c'est la même chose que en "console", sauf que les bois sont intégrés aux bâtis !
Les exemples les plus courant, sont les colombages, les portes de granges, volets etc !
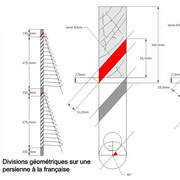
Le principe est utilisé couramment dans le calage des vitrages contemporains sous la dénomination de "à la française) , ci qui maintient l’équerrage des menuiserie dans le temps .
Attention au sens des écharpes, toujours du haut coté serrure et en bas coté ferrage (charnières) 
La parfaite boulette (écharpe à l'envers)!!  thibaultflorki...orte-a-echarpe/
thibaultflorki...orte-a-echarpe/
Discutions intéressantes sur l'air du bois :
A suivre
Rappel : L' art du trait ! Dessins, plans, épures ....
Avant d'aller plus loin sur les tracés géométriques et leurs utilités appliquées à nos métiers, nous devons nous remémorer à quoi cela nous sert !
L'art du trait
En 2009 l'UNESCO inscrit « la tradition du tracé dans la charpente française » (dit art du trait), cela dit tout les corps de métiers qui battissent ou construisent des choses en volumes, doivent se servir de cet art ancestral, qui va de la géométrie plane jusqu'aux "tracés dans l'espace" (3D).
L'arrivée de l'infographie a révolutionner les moyens , tout en effaçant des pans entier de cet art ancestral !
Pour en avoir parlé avec lairdubois.fr/@dasnevej, je pense maintenant que l'un ne va pas sans l'autre!
Maîtriser l'art du trait permet de se familiariser à l'infographie plus facilement grâce à des automatismes acquis traditionnellement, si j'en crois mon expérience.
Mais le contraire existe, puisque dessiner des projets ambitieux sur sketchup et ne pas pouvoir les réaliser si on ne connais pas l'application sur épure de fabrication échelle 1, c'est très bête non ?!  Donc on y reviens toujours !
Donc on y reviens toujours !
Je me permet donc un petit rappel ici de ce que l'on utilise professionnellement !
Le dessin d'art : Le dessin d'art est une technique de représentation visuelle sur un support plat. Il désigne l'action de représenter un objet quelconque, sans cotations ni techniques particulières afin de définir en situation ou non le projet d'un ouvrage ! (dessin, peinture, etc )
Le dessin main levée: Complet ou partiel sans recherche artistique, sur lequel on applique des cotes générales et des détails de formes à main levée.
Si ce dessin ce concentre sur du détail particulier ou des fonctions, ce dessin se nomme alors un croquis coté et/ou un schéma !
Très facile a tracer sur du papier bloc à petits carreaux 5/5 mm
Le dessin en perspective: Tracé académique aux instruments, il permet une représentation très détaillée d'un projet en situation, avec des proportions réelle avec points de fuites ( comme une représentation photographique), mais ne permet pas de prendre des cotations utiles dans sa fabrication !
Majoritairement remplacé par l'infographie .
Le dessin industriel, plan ou étude : C'est un dessin orthogonal à échelle réduite, qui défini toutes les faces d'un ouvrage, avec cotations et détails de fabrications (coupes, sections, etc.) !
Initialement il est tracé sur format normalisé "à la planche" et instruments .
Dés que l'on part de la vue en plan et d'un développement pour projeter des points, on parle de dessin géométral et de stéréotomie !
Art du trait maîtrisé ici: dumetier.org/e...d74574d472af835
Majoritairement remplacé par l'infographie, mais encore nécessaire en taille de pierre, escaliers, charpente , etc !
Le plan sur règle: C'est une représentation des éléments d'un ouvrage vus en coupes ou sections horizontales et verticales, à l'échelle 1, de manière a représenter des cotes de fabrications ainsi que des détails de fonctionnement (Arasements, jeux, quincailleries, panneaux, déviations d'assemblages ect.)
Elle se trace précisément sur une "règle" bien droite et parallèle, avec les instruments (équerre et un"trainard")! Celle ci, peut aussi servir a tracer une épure ! voir ci dessous .
Une épure : C'est une représentation échelle 1 d'éléments non transposables depuis un plan échelle réduite d'origine.
Elle se trace sur un grand support (ex panneau cp ou mélaminé en menuiserie,ébénisterie) ou directement au sol (charpente)
Elle est figurée que de traits utiles à la prise de cotes, tracer des gabarits, ou à "piquer" les points utiles en y positionnant directement les bois !
Les cintres, peuvent être directement tracés sur les bois au crayon depuis le point de centre avec un compas à verge, ou directement "pré-découpés" précisément:  à la défonceuse avec un montage axé !
à la défonceuse avec un montage axé !
ici le principe : youtube.com/wa...h?v=gdmN4-ZnF-E
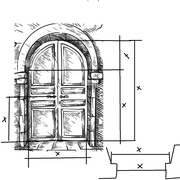
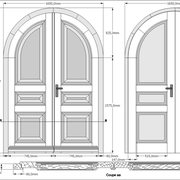
Ci dessous, illustration de chaque type de représentation expliquées dans cet article sur un même thème, (ex: une porte double en plein cintre) pour une lecture plus facile des différences !
Les polygones réguliers utiles dans nos épures : Introduction
Les polygones réguliers sont des figures géométriques planes, formées de plusieurs cotés construites majoritairement dans un cercle .
Dans nos métiers, nous utilisons ces polygones réguliers qui seront tracés à base de segments identiques, reliés par des angles identiques !
Le plus simple étant le triangle équilatéral (trois cotés identiques et trois angles à 60°) et le plus complexe étant logiquement par définition, le cercle à 360 cotés et 360 angles à 1° .
Entre ces deux extrêmes, nous utiliserons plutôt le carré (4 cotés), le pentagone (5 cotés), l'hexagone (6 cotés), l'heptagone (7 cotés), l’octogone (8 cotés), et parfois le Ennéagone (9 cotés) .
Des multiples par bissectrices d'angles peuvent être fait depuis ces simples figures, ce qui est amplement suffisant dans des dessins d'études ou d'épures !
D'autres plus complexes, sont utiles en mécanique, horlogerie, ingénierie, ect .(Engrenages)
Le triangle et le carré :
Nous en avons déjà parlé précédemment, juste en rappel que les coupes d'assemblages sont à 30° pour le triangle équilatéral et 45° pour le carré ! (bissectrices des angles)
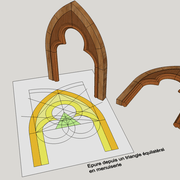
Ci dessous des exemples d'épures à base de triangles équilatéraux ! En résumé, pas de limites donc apprenez en vous amusant !
Les polygones réguliers utiles dans nos épures (suite).
Le pentagone
En géométrie plane, un pentagone régulier est un polygone à cinq sommets, donc cinq côtés et cinq diagonales, identiques !
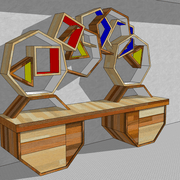
Dans nos professions l'utilité du pentagone réside surtout a élaborer ludiquement des travaux singuliers, qui obligent à la réflexion aussi bien pour le praticien que pour le détenteur d'un ouvrage pentagonal !
Le tracé du pentagone est très précis et intéressant, de plus il permet ensuite le tracé du décagone (10 cotés) , utile dans des pièces multiples a l’intérieur d'un pentagone ou d'un de ses secteurs (ex des pieds)
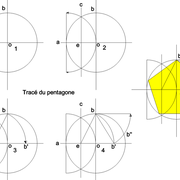
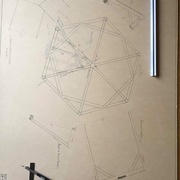
Le tracé du pentagone régulier :
1/ Nous traçons le cercle désiré de base avec ses deux diamètres perpendiculaires (a-b)!
2/ Avec le compas ouvert au rayon du cercle, nous élevons une perpendiculaire "c" depuis le diamètre "a" ,ce qui nous donne le point "e" .
3/ Depuis "e" comme centre, au compas nous projetons "b" en "b'" sur le diamètre "a"
4/ Depuis "b" comme centre, nous projetons "b'" sur la circonférence du cercle pour placer
"b""
5/ Le segment (b-b") étant le coté du pentagone, nous le reportons au compas sur la circonférence du cercle pour tracer la figure finie !
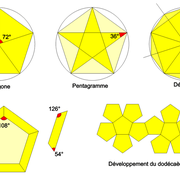
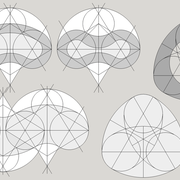
Particularités utiles du pentagone:
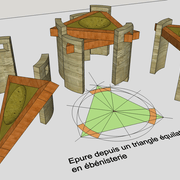
Ci dessous, les différents angles présent dans le pentagone, le tracé du décagone, et le développement du dodécaèdre (solide à 12 faces pentagonales)
lairdubois.fr/...ns/?q=pentagone
lairdubois.fr/...as/?q=pentagone
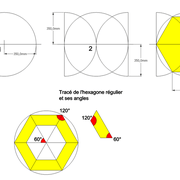
L'hexagone
Un hexagone régulier est un polygone convexe dont les six côtés ont tous la même longueur et des angles aux sommets identiques à 120°.
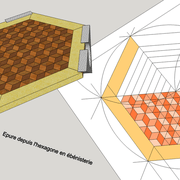
Comme les carrés et les triangles équilatéraux, les hexagones réguliers permettent un remplissage d'un plan. (ex: Les pavages de sol carrés et hexagonaux des tomettes en terre cuite, ou des décors en marqueteries)
Dans nos professions, c'est pour ainsi dire le polygone complexe le plus utilisé en épures, pour la facilité et précision du tracé initial ! Sachant que les cotés sont égaux au rayon du cercle .
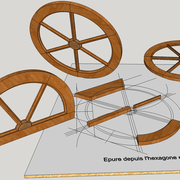
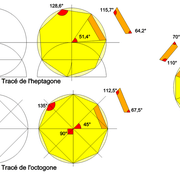
Le tracé de l'hexagone régulier :
Ici deux arcs de cercle depuis le diamètre avec le compas ouvert au rayon, suffisent a tracer très précisément les points de segments des 6 cotés de la figure !
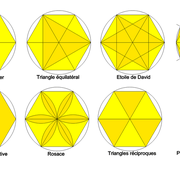
Depuis le tracé de base, il y a une source infinie de combinaisons et de motifs géométriques utiles ! (Ex: la célèbre grande rosace de la cathédrale de Notre Dame )
lairdubois.fr/...ns/?q=hexagonal
L'heptagone
Un heptagone régulier est un polygone à sept sommets, sept côtés, et sept angles égaux !
Tres peu utilisé dans nos métiers, car sa construction est approximative, et l'on doit cheminer plusieurs fois le réglage du compas sur la circonférence du cercle !
En effet , le segment né de la construction est légèrement inférieur à sa mesure juste !
On fait quelques travaux de progressions à l'aide de l'heptagone, afin de compliquer les épures, donc pimenter le travail !
L'octogone
Un octogone régulier est un polygone a huit sommets, dont les huit côtés ont la même longueur et dont les angles internes sont égaux.
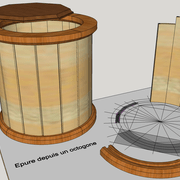
Apres l'hexagone, l'octogone est le polygone le plus utilisé par sa facilité et précision de son tracé!
Dans nos professions du bois, on en fait pratiquement les mêmes applications que pour l'hexagone, plutôt dans des travaux de plus grande ampleur, car ce dernier nous apporte plus de points d'assemblages !
lairdubois.fr/...ons/?q=octogone
L'ennéagone
Un ennéagone appelé aussi nonagone est un polygone à 9 sommets, donc 9 côtés et 9 angles internes égaux .
Memes choses que pour l'heptagone, la construction est très complexe, pour un résultat approximatif !
Toutefois, avec un bon rapporteur, on arrive à des tracés correct, car ses angles intérieurs sont de 40°
En résumé :
En 40 ans de métier, je n'ai tracé qu'une fois un heptagone et un ennéagone, pendant mon apprentissage sur mon classeur de géométrie ! Et maintenant pour vous
! Et maintenant pour vous 
Et donc, à vos compas et règles, et surtout éclatez vous avec les polygones !  exemples ci dessous !
exemples ci dessous !
Pour l'anecdote, j'ai connus l'inventeur du ballon de foot en bois à base de pentagones et d'hexagones. Il s'agit du Pays Esteban , Compagnon du Devoir menuisier Bordelais, avec qui j'ai partager quelques bons moments sur le tour il y a 40 ans à Nimes
Il a fait cette série de ballons officiel pour la coupe du monde 1998 !
auction.fr/_fr...morant-16959256
lairdubois.fr/.../?q=ballon foot
lairdubois.fr/.../?q=ballon foot
Ellipses, ovales, oves et anses de paniers, utiles dans nos épures
Ovoide ?
Définition géométrique qui inclue dans le sens étymologique œuf ou une forme d'œuf en latin , une ellipse, un ovale, une ove !
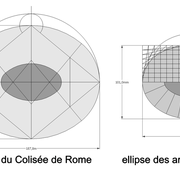
Commençons par une petite question ? Ci dessous nous avons deux photos de monuments prestigieux de l'époque romaine !
A savoir :
Le Colisée de Rome, qui est un immense amphithéâtre ovoïde
Dimensions externes Longueur : 187,75 m Largeur : 155,60 m
Dimensions de l'arène Longueur : 86 m Largeur : 54 m
Les arènes de Nîmes, qui est un amphithéâtre ovoïde de 133 m de long sur 101 m de large, avec une Dimensions externes Longueur : 133 m Largeur : 101 m
Dimensions de l'arène Longueur : 69 m Largeur : 38 m
Géométriquement, quelle est la différence entre ces deux monuments magnifiques ?
La réponse est que, le Colisée est tracé avec l'ovale et que l’arène de Nîmes est tracée en ellipse ! 
Pour résumer cette constatation, c'est que un ovale de part sa construction géométrique, permet de tracer toutes courbes parallèles internes ou externes à sa circonférence depuis des mêmes centres !
Alors que la construction d'une ellipse ne permet que de tracer sa circonférence ! En effet Les parallèles ne peuvent être tracées que par des projections de points d’équerre tout au long de sa courbe ! (Trusquin à semelle deux points)
Depuis l'antiquité a nos jours, on utilise régulierement les formes "ovoïdes", à l'image de la belle structure ci dessous ! 
L'ellipse
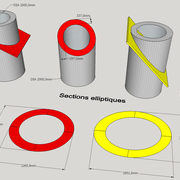
En géométrie, une ellipse est une courbe plane fermée obtenue par la section d’un cylindre de révolution avec un plan incliné (ex raccords de tuyauteries).
L'ellipse par conséquent représente un "ovale parfait"! Par contre comme déjà indiqué plus haut, des courbes parallèles ne peuvent être tracés que par points, ce qui prend beaucoup de temps, en plus d’être reliés avec instrument appelé un "pistolet ou perroquet" ou une "cerce" (règle semi rigide) à l'atelier dans les grandes constructions 
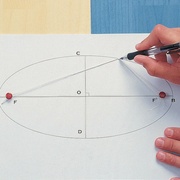
Tracé de l'ellipse au cordeau :
Bien connu des jardiniers, ce principe est simple et efficace, par contre il n'apporte pas la précision requise dans nos professions !
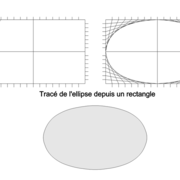
Tracé de l'ellipse depuis un rectangle :
Cette technique est intéressante, il suffit de partager un rectangle en quatre quartiers, sur lesquels on traces des divisions en nombres égales sur le grand coté et le petit coté !
Il suffit enfin de joindre par des droites les divisions réciproques, leurs intersections modélisant les points à relier au pistolet .
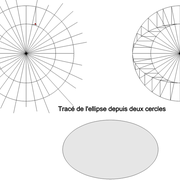
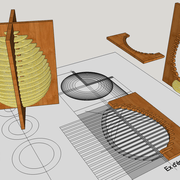
Tracé de l'ellipse depuis deux cercles :
C'est la construction la plus précise, il suffit de tracer deux cercles concentriques correspondant au deux mesures grand axe/petit axe désirés de l'ellipse finale .
Après avoir choisi leurs rayons respectifs (huit par quartiers à la volée) Les diamètres des deux cercles étant les axes de l'ellipse.
Nous traçons ensuite des lignes d'aplombs à chaque rayons du grand cercle, qui se couperont avec des lignes de niveaux de chaque rayons réciproques du petit cercle!
Enfin à l'aide du pistolet, nous traçons la courbe finale de l’ellipse .
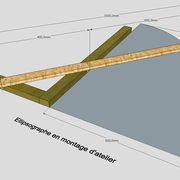
Tracé de l'ellipse depuis un ellipsographe :
Ce sont des montages articulés, qui permettent de tracer des courbes elliptiques en un seule fois très précisément !
On peut aussi y installer une défonceuse afin de découper ou pré-découper en direct des bois ! 
youtube.com/wa...h?v=JlGADVaItv8
Ci dessous des articles autour de l'ellipse sur l'air du bois !
lairdubois.fr/...ions/?q=ellipse
lairdubois.fr/...-pas/?q=ellipse
lairdubois.fr/...lans/?q=ellipse
L'ovale
Étymologiquement, un ovale est une forme d'œuf. En mathématiques, l'ovale n'est pas vraiment défini de manière académique !
En résumé, comme un ellipse, un ovale est composé de courbes autour d'un grand axe et d'un petit axe perpendiculaire !
Par contre , la construction géométrique de l'ovale permet de faire des courbures parallèles depuis les mêmes axes , facilitant ainsi le tracé des épures !
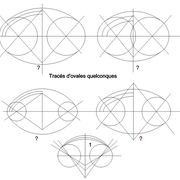
L'ovale quelconque :
C'est la construction la plus simple, mais pas nécessairement proportionnée !
En effet nous pouvons partir d'un grand axe connu, sur lequel on trace des cercles à volonté, puis par constructions depuis les axes de ces derniers, nous les raccordons par les grandes courbes.
Comme nous le voyons sur l'illustration, tout est à peu près possible, mais nous ne pouvons pas déterminer un petit axe précis, mais juste par tâtonnements s'en approcher en décalant l'axe à volonté (fig 1) !
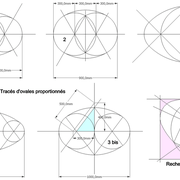
L'ovale proportionnés :
Ici les constructions sont "normées" , elles permettent des ovales proportionnés de formes plus fluides !
1-2/ Par cercles et grand axe connus :
En divisant le grand axe connu par deux et en y traçant trois cercles d'intersections (trois diamètres), ou en divisant le grand axe connu par trois et en y traçant deux cercles d'intersections (deux diamètres) .
3-3bis/ "A la romaine" par cercles quelconques sur le grand axe connu, mais la recherche des centres des grandes courbes avec triangles Pythagore (3-4-5)
4/ Tracé avec petit axe connu , depuis un cercle de diamètre équivalant au petit axe !
5/ Recherche du centre d'un ovoïde en traçant un rectangle tangent .
Puis tracer un cercle déterminant 4 points d'un quadrilatère afin de déterminer les deux axes de l’ovoïde.
Cette construction permet de le retranscrire précisément construit pour une épure (ex prise d'un gabarit à la volée sur le chantier ou un mobilier)
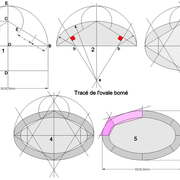
L'ovale borné :
C'est celui qui nous est vraiment utile dans nos travaux, car nous pouvons tracer un ovale de petit et grand axe connus, se rapprochant de l'ellipse, tout en permettant des constructions avec des parallèles !
C'est en fait le tracé de l'anse de panier en miroir ! (mais nous y reviendrons plus tard) 
1/ Apres avoir tracé les deux axes AB et CD perpendiculairement aux cotes désirées, nous traçons un arc de cercle de centre AOB, qui nous donne le sommet E.
Depuis C comme centre, par arc de cercle, nous rabattons E sur les segments AC et CB .
2/ Depuis les centres des segments AE et BE, nous élevons des perpendiculaires, qui se croiseront sur l'axe CD en petit a .
Sur le grand axe vertical après cette construction, nous trouvons le centre de la grande courbe de l'ovale en petit a, et sur le grand axe les deux points petit b, nous donnant les axe des petites courbes .
En traçant des fuyantes en alignement des perpendiculaires, nous obtenons les lignes de raccordements ds courbes !
3/ En reportant cette construction en miroir, nous obtenons le tracé complet de l'ovale .
4/ Depuis la construction, nous pouvons a volonté tracer des parallèles utiles dans nos travaux ! 
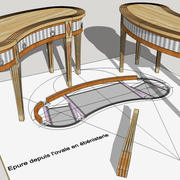
5/ En traçant tangentiellement aux segments donnés par les lignes de raccordements, nous avons les bloc capables de débit, accueillant les pièces cintrées utiles !
L'ove
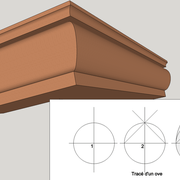
Un ove (terme utilisé en architecture et en orfèvrerie) est un motif ornemental en forme d'œuf qui orne une corniche ou une moulure.
Dans nos professions, ce qui est en forme d’œuf tracé géométriquement !
Il est très peu utilisé dans nos ouvrages , mais ludique à dessiner et inventer des objets de formes d'oves!
L'anse de panier
Une anse de panier est, en géométrie, une courbe plane fermée tracée au moyen d’arcs de cercle, en nombre impair, utilisée en architecture et principalement dans le domaine des ponts et voûtes .
Sa forme ovoïde présente une variation de courbure continue depuis sa naissance jusqu'au sommet, c'est-à-dire depuis les extrémités du grand axe jusqu’au sommet du petit axe.
Comme expliqué dans le chapitre précédent de l'ovale, une anse de panier représente par conséquent un demi ovale !
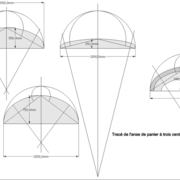
L'anse de panier à trois centres :
Elle est employée couramment dans nos professions, surtout dans le bâtiment en divers éléments construits par les menuisiers, charpentiers, maçons, plâtriers, tailleurs de pierres, ect , Pour son esthétique et la facilité de la tracer !
Elle à évidement la particularité d’être bornée par un grand axe connu et son petit axe (hauteur) connus . De plus on peut y tracer à volonté des courbes parallèles (1) !
je ne reviens pas sur son tracé déjà décrit dans l'ovale ! 
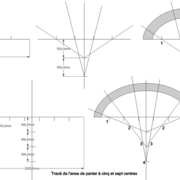
L'anse de panier à 5-7-9-11 centres :
Connue des tailleurs de pierres, qui l'utilisent régulièrement, car elle se rapproche le plus de la courbe parfaite de l’ellipse, et permet de tracer des parallèles .
Elle à un ratio de solidité supérieur !
Elle est facile à tracer, mais ne permet pas de borner le petit axe !
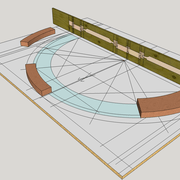
En résumé, on trace l'anse de panier en fonction de son grand axe désiré, puis on détermine les hauteurs désirées depuis le sol ! (ex ci dessous en menuiserie et en charpente)
La manière de la tracer, est de diviser le grand axe en 5-7-9 ou 11 parties égales, puis de les reporter en fonction sur l'axe vertical . Les intersections , sont les centres des arcs de cercles formant la courbes finale de l'anse de panier .
lairdubois.fr/...=anse de panier
En résumé, avec les ovoides, il y a un grand champs de créations possibles, à vos crayons ! et à suivre !
autre lien intéressant :
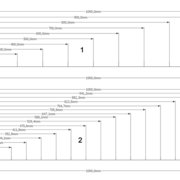
Tracés de divisions !
Les divisions
Les divisions dans les tracés d'exécutions d'ouvrages, sont légions!
En effet balustres d'escaliers, petits bois de fenêtres et autres chevronnages, posent souvent des soucis aux novices et l'on se retrouve souvent en "galère" quand au troisième tracé on est encore pas précis !
Nos allons essayer de remédier à cela ! Des tracés et procédés spécifiques existes pour gagner en temps et précisions . En règle générale, ne faire qu'un tracé précis ,et en une seule fois !
Des tracés et procédés spécifiques existes pour gagner en temps et précisions . En règle générale, ne faire qu'un tracé précis ,et en une seule fois !
Divisions de segments :
Tout d'abord, un principe simple à mettre en oeuvre chaque fois que c'est possible!
Nous devons prendre et tracer des points de mesures sur nos bois avec un réglet, un mètre ruban, un décamètre fixes, et toujours des mesures progressives multiples .
1/ La figure 1 le principe, nous démontre une division tracée (connue) sur un segment de un mètre à diviser en 10 parties égales avec l'outil de mesure fixe !
On aperçois la précision de la technique (100 mm, 200 mm, 300 mm, etc)
2/ Dans l'exemple 2, on découvre le même principe avec une mesure de segment X divisée en x parties égales!
Ici on se sert d'une calculette et sa fonction mémoire :
Nous prenons la mesure du segment à diviser, puis avec la calculette nous divisons la longueur par le nombre de divisions désirées .
Le résultat est mis en mémoire (touche M+) .
Enfin, chaque fois, nous ajoutons la mémoire au dernier résultat (touche RM).
Il suffit alors de pointer chaque fois le résultat afin d'avoir des divisions constantes .
3/ Par divisions géométriques, principe souvent utilisé car sans calculs ! (Thales)
Sur un segment (a-b) à diviser en x parties égales désirées, nous traçons une droite biaise (c) depuis (a) quelconque !
Sur cette dernière, nous traçons au compas le nombres de divisions désirées, mais arrondies plus grandes que le calcul de divisions finales. (ex divisions calculées 246 mm, on arrondi à environ 260 mm)
Par une droite reliant la dernière division et le point (b) du segment, nous trouvons un angle a prendre avec une fausse équerre ou sauterelle, puis à l'aide de cette dernière nous traçons des parallèles aux divisions sur (c) qui nous donnent les divisions finales très précisément de notre segment (a-b).
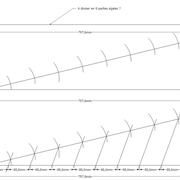
En résumé, ces deux options paraissent logiques, mais dans le métier, il faut chaque fois prendre en compte les largeurs des pièces a diviser ! 
En effet, ne pas les prendre en compte, nous ne diviserons que des axes, et en y plaçant ensuite les bois, on s'aperçois que le tracé est faux !
Ci dessous, l'illustration 3, exemples qui nous démontrent le principe de base de divisions arithmétiques et géométriques avec les bois pris en compte dans les tracés utiles, que nous allons approfondir plus loin !
Applications de divisions avec prise en compte des bois !
Ici la pratique professionnelle ancestrale sur divers travaux spécifiques! nous allons étudier les différentes façons de faire que l'on rencontre le plus communément !
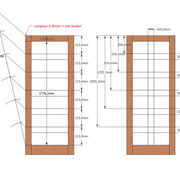
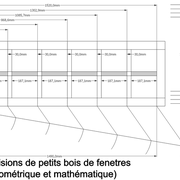
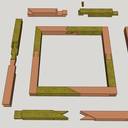
Divisions géométrique et arithmétique des petits bois:
Dans l'illustration nous prendrons un bâtit principal en section de bois 60 mm de largeur, et de petits bois "croisillon" en 30 mm de largeur !
Les deux principes de divisions géométrique et arithmétique, nous montre l'utilisation d'une largeur supplémentaire de petit bois tracée outre le vide du bâtit.
En effet, nos divisions seront parfaitement égales, en un seul tracé ou il sera simplement ajouté par superpositions des bois pour tracer les mortaises ou entailles croisillons .
De plus les petits bois montants intermédiaires, auront tous les mêmes arasements bien calibrés
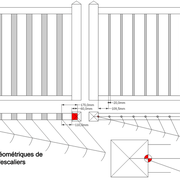
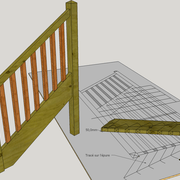
Divisions géométriques de balustres et barreaudages :
Pour des balustrades et garde corps , il faut partir de divisions maximum 110 mm de vide entre deux éléments de sécurité (balustre ou barreau)!
Pour des balustres de section carrée ou rectangulaire, nous procédons comme pour les petit bois, à savoir que l'on ajoute un balustre hors arasement d'un des poteaux suivant le multiple approchant 110 mm max .
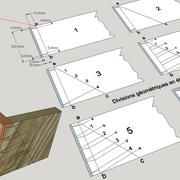
Divisions géométriques de queues d'arondes d'ébéniste:
1/ La largeur et l'about d'équerre de notre pièce est dessinée, puis nous y traçons parallèlement à l'about l'épaisseur du bois à assembler (a-b) ici 20 mm !
Nous traçons ensuite les tenons de rives en fonction de leurs proportions calculées de 1/5.
2/ Nous traçons classiquement maintenant une diagonale quelconque fuyante (a-c).
3/ Sur la diagonale quelconque, nous traçons 4 divisions correspondantes au nombre de queues définies par la formule de calcul . (ici au réglet en ligne 30/60/90/120 ), on peut aussi se servir du compas évidement.
Puis nous relions la 4 eme division avec l'extrémité de la pente du tenon de rive inférieur.
4/ Nous traçons toutes les parallèles à (b-4) depuis les points 3-2-1 !
Puis en parallèle nous traçons d'autres divisions avec la même mesure de 30 mm ou du même écartement de compas depuis l'extrémité de pente du tenon supérieur placé sur l'autre l'autre rive de la pièce , que nous nommerons a/b/c/d.(théorème de Thalès).
5/ Parallèlement aux pentes des tenons de rives préexistants, avec une fausse équerre ou un rapporteur, nous traçons toutes les joues des queues d'aronde.
6/ Nous matérialisons les enlèvements pour découvrir visuellement nos queues d'arondes de l'assemblage d'angle parfaitement équilibrées prêtes à être taillées une fois tracées sur nos bois .
En résumé, comme pour les exercices précédents, ce tracé devra être fait en amont du tracé final directement sur un des bois qui servira de référence en cas de tracés multiples.
Autres exemples
Ce pas à pas présente un projet en cours de réalisation.















































Discussions
Direct dans mes favoris !
C’est super tous ces liens qui font découvrir des articles forts intéressants.
Merci sylvainlefrancomtois
De rien ! C'est de la transmission d'un art, c'est juste passionnant de partager, et faire perdurer celui ci (devoir)
Bel esprit sylvainlefrancomtois, qui t'honore.

Merci !
N’y aurait-il pas un soupçon de préjugé à prétendre qu’un ouvrage à caractère académique est par définition “indigeste” ? Ou serait-ce une conséquence d’un système d’éducation à vocation hélas trop élitiste qui laisse des traces ?
Commentaire à prendre avec du recul, mon intention n’est pas polémiste.
Cordialement, Filou
Je prend pas mal ! au contraire, les grands ouvrages sont à lire quand on apprend évidement, mais une synthèse sur ce que l'on utilise couramment est à mon gout un moyen pédagogique plus compréhensible pour des novices et amateurs !
au contraire, les grands ouvrages sont à lire quand on apprend évidement, mais une synthèse sur ce que l'on utilise couramment est à mon gout un moyen pédagogique plus compréhensible pour des novices et amateurs !
Les fondamentaux, peuvent être bien sur approfondis en fonction des besoins et des envies, à mon avis !
sylvainlefrancomtois +100
Dans une société qui privilégie le ludique (voire même le futile…) à l’académique, un retour sur les connaissances fondamentales (oui oui) fait un bien fou à mes neurones engourdis
Merci sylvainlefrancomtois pour ce cours de géométrie appliquée
Quant à mon cahier d’atelier, c’est un aide mémoire très précieux pour éviter de réinventer tous les réglages de fraiseuse …
Emmanuel Libaudiere
Un grand merci pour cet article qui va, je n'en doute pas me permettre de compléter ce fameux cahier d'atelier déjà présent dans mon tiroir d'établi. D'ailleurs, je l'ai en double, j'en ai également un exemplaire dans mon bureau où je réalise mes plans, gabarits, etc.
Merci beaucoup
Merci papa ça me sera bien utile


en fait c'est un peu grâce a toi que j'ai eu cette idée !
Encore un pas à pas qui va s'avérer précieux !
Merci Sylvain !
J'ai liké avant de voir ce dont il s'agissait.
On avait déjà eu droit au cahier de kaj (qui a servi de base au mien)
et plus modestement mais plus ancien celui que j'ai sauvé d'une déchetterie :
Nul doute que celui ci sera fort intéressant aussi.
Hello, je pensais les mettre en liens au moment opportun des prochains articles !
C'est mon côté Attila, je coupe l'herbe sous le pied trop tôt...
(désolé)
Bah voilà, merci sylvainlefrancomtois et trente six seb ! Je me suis créé une collection de cahiers d’atelier.. du bon sens, du partage et de l’inspiration
Très bon quelques rappels intéressant rafraîchi la mémoire
Super!
Très instructif, bravo.
Bravo, belle idee,
Merci.
Merci sylvainlefrancomtois pour ce cahier inélectrique, mais bourré d'énergie.
essentiel et en sus cela nous rajeunit en nous replongeant dans nos cours de géométrie
Merci pour ce travail salutaire, unitaire et qui deviendra légendaire !
pour ce travail salutaire, unitaire et qui deviendra légendaire !
Merci,
Merci pour ce partage. Certains rappels sont toujours bons à faire car toujours utiles
wouah, super, merci
ca me rapelle un bouquin d'atelier mécanique (vitesse des machines etc) j'essaye de remettre la main sur ce pdf qui se ballade sur le woueb, pour le mettre en trouvaille (même si il se révèle peu utilisable pour l'atelier bois)
j'aime feuilleter ces choses qui sont parues pour aider à rester efficace, ne pas perdre de temps et éviter les erreurs même quand on a la tête bien enfoncée dans le guidon.
edit j'ai retrouvé le nom du bouquin, je ne vais pas l'associer á l'AdB: pas certain qu'il soit dans le domaine public et puis finalement c'est très spécifique à la mécanique (et ce qui ne l'est pas figure certainement dans une forme plus adaptée dans le présent pas à pas)
un pdf de truc et astuces géo a utiliser a l'atelier joho.p.free.fr...UES DE BASE.pdf
sylvainlefrancomtois je trouve exagéré de déprécier le travail d'une personne en rendant public l'adresse www de son site ou apparaît l'écharpe à l'envers
(rien sur le bien-fondé de votre remarque juste sur la contre publicité publique)
je me permet de vous joindre une photo qui dit la même chose sans toucher à la personne.
encore merci pour la pertinence de vos publications, au plaisir de continuer a vous suivre,
bien à vous
fr Moreau
hello MoFran
Perso, professionnellement c'est pas entendable, de plus il a mis un petit texte pour essayer de se défausser de son erreur !
Il dit une porte de 40 kg c'est pas rien , et il a tout collé (cette porte doit etre un tonneau ou voilée avec le temps !
Une erreur ou une faute ça s'assume, c'est ce que je fait quand je fais des erreurs depuis toujours,
Ce sont les règles de l'art qui priment .
Imagine une soudure à l'argon de chaudronnier faite avec radiographie pour du nucléaire ! et que le gars fasse une boulette en disant ouvertement que il a fini sa soudure à l'arc car il lui manquait de la matière !
Et qu'il explique que le résultat visuel est identique ?
sylvainlefrancomtois merci pour votre réponse
je suis personnellement entièrement d'accord, c'est juste qu'on est sur la place publique et qu'il a l'air de s'être investit dans la promotion de son travail (plus que dans la réalisation ok) et que en dehors de la leçon qu'il ou qu'un autre aurait a en retirer (je devrais aller vérifier mes volets, je ne sais plus comment je les ais montés) , cet investissement donc á propos de son image numérique lui appartient et comme ici c'est les règles de l'image qui priment (on est pas sur le darkweb) je me permets de le relever (sans en faire plus), bien á vous
Une belle idée signée Sylvain
merci Jacky!
Pour trouver le centre d'un cercle ou d'un arc de cercle, il y a aussi la brillantissime Méthode de Napoléon:
+1

Bravo, rien à dire, tout y est.
Merci Sylvain
Un gros merci
merci pour la contribution relative aux cercles et disques !
Bonjour, sur la dernière image sur le calage des vitrages "à la française", je ne parviens à lire la phrase qui commence par "Espace...". Serait-il possible de nous la transcrire ?
Merci beaucoup
Amicalement,
Manuela
Espace a forcer un peu ! (mettre en pression)
sylvainlefrancomtois Merci beaucoup
0,866. 1,732. 1,414.......
...
G+2H=64.......
0.707, 1.154, 0.577

sylvainlefrancomtois
Oui Sylvain certain d'entre nous ont cela en mémoire et savent s'en servir... ces derniers ont-ils besoins d'un cahier? tu forces l'admiration de vouloir enseigner, voire rappeler le comment et le pourquoi. Merci
Merci de ta réponse Elle m'a obligé à chercher!
Pendant longtemps la règle à calcul GRAPHOPLEX a été ma compagne, aujourd'hui je ne suis pas sur de me rappeler toutes ses fonctionnalités mais à l'époque elle m'était indispensable je ne me vois pas aujourd'hui expliquer "comment ça marche"
Pour l'occasion je l'ai ressorti d'un tiroir poussiéreux. Impeccable, elle coulisse parfaitement, elle ne demande qu'à servir.
racmterrof
Ah les Règles de Calculs Graphoplex.... j'en ai 3 : 1 ordinaire pour la poche, 1 classique complète et une pour le Calcul des armatures pour poutres B.A.... +celle pour le Topigraphie. Tout cela bien pratique. Puis il y a eu la HP41CV avec Cartes Magnétiques pour y stocker des mini-programmes de calcul (95 % env du B.A.). Eh oui, on commencer à faire de la Programmation !!
Et oui tout ça était bien pratique sur Chantiers....
JPA33
Merci pour ton commentaire. Je n'ai pas retrouvé ma règle de poche.
Deux règles m'ont accompagné, la photo (pas retrouvé le curseur) et celle de poche.
Waouw, mon grand père m’en avait donné une, et je n’ai malheureusement pas eu le temps d’apprendre avec lui comment et pourquoi m’en servir.
Je serai peut être moins con devant cette règle à coulisse maintenant
Cortocox En tout cas bien pratique...... sans connexion !
Et on était bon sur les Echelles Logarithmiques !!
Il y a environ 2 ans, j'avais appris que Graphoplex avait été repris par une société étrangère. A voir avec Google....
Cortocox Il y a pas mal de tutos sur le net qui explique comment utiliser une règle à calcul.
Le principe repose sur les logarithmes et la relation log (a x b) = log a + log b.
Quand on veut multiplier deux nombres, on les transforme en log, et il suffit alors de les additionner. Si on prend deux règles où les nombres sont sur une échelle logarithmique, il suffit d'additionner les longueurs sur les règles, pour trouver la multiplication (ou la division).
J'ai été de la dernière génération à passer le bac avec une règle à calculer. L'année suivante, les calculatrices étaient autorisées. J'aimais bien, c'était rigolo. Cela ne donnait pas les unités, donc, il fallait un peu de jugeote pour rajouter le nombre de zéros, ou mettre les virgules. Cela obligeait à vérifier la cohérence de ses calculs. On était un peu plus intelligent avec ça...
Et on est quand même allé sur la Lune avec ce genre de machin...
Kentaro Excellent !
Merci pour la découverte !
Je sais pas si j'irai sur la lune (a priori y a pas de bois là bas donc je vois pas bien ce que j'irai y foutre ...!) mais du coup j'ai trouvé une règle à calcul sur eBay pour 10 euros.
Hâtes de creuser le sujet.
Et en cherchant je suis aussi tombé sur une "règle à calcul Omaro" sur les expressions trigonométriques ! Visiblement nous qui nous donne les sin, cos, tan des angles sans recours à la calculatrice.
racmterrof
Kentaro
dependancesbois
dependancesbois Génial! Tu devrais bien t'amuser!
Il y avait aussi les tables de trigo, en carton marron:
delcampe.net/f...-354925095.html
J'en ai encore une à l'atelier, que j'utilise souvent.
Kentaro Oh oui ces fameuses tables!
Oui je vais bien m'amuser sur chantier avec ça plus un boulier pour faire les factures devant les clients !
Là je les achève après les outils à main !
Kentaro c'est celle que j'avais aussi ! (déjà + 40 ans)
sylvainlefrancomtois avec la règle à calcul pas besoin de table de trigo, lecture directe.
J'ai reçu ma règle à calcul et de Trigo ! C'est juste génial ! )
)
La modernité de l'électronique fait vraiment disparaitre des systèmes ingénieux !
(Encore un pas vers la décroissance !
Ton idée de départ est excellente. Elle me rappelle les "aides mémoire TECHNOR" qui ont longtemps été mes compagnons.
L'aide mémoire est destiné à quelqu'un qui a une absence momentanée. Il retrouvera aisément dans un FASCICULE le détail qui lui échappe pour poursuivre l'ouvrage en cours.
En quelque sorte l'aide mémoire, le pense bête..... est l'antiseche du
Sachant.
Pardon pour ce chiasme loupé
je connaissais pas !
ici un fascicule écrit par le célèbre jacques heurtematte ! ebay.fr/itm/39...T4AAOSwBpNh1wtm
Étonnant!
racmterrof je viens de l'acheter pour ma fille !
sylvainlefrancomtois bon choix, on est aussi dans le principe de l'aide mémoire.
trente six seb oui c'est bien fait , y a méme des pages vides pour ses propres notes !
sylvainlefrancomtois
l'pdf traîne sur internet
dneis J'en ai acheté un pour ma fille !!
sylvainlefrancomtois je l'ai aussi en version papier. Top.
Super merci Sylvain !
Merci sylvain ! Très bon travail.
Sylvain tu nous fait toujours un énorme travail
c'est réciproque !
magnifique! comme toujours!
Bravo Sylvain pour ces nouvelles études géométriques et pratiques de ces Courbes.....
Mais je te pose une question concernant l'Ellipse : Comment s'appelle une Courbe //le à l'Ellipse, Extérieurement et/ou Intérieurement ?... Pourquoi ? Et la/les avantage(s) de cette dernière en pratique ?
hello L'ellipse ne peut pas avoir de parallèles par son tracé , il faut donc les tracer obligatoirement par trusquinage, ce qui est chronophage et peu fiable ! mais on peu s'amuser ! (ex ma table de cuisine en photo est fabriquée en ellipse)
(ex ma table de cuisine en photo est fabriquée en ellipse)
sylvainlefrancomtois
"...L'ellipse ne peut pas avoir de parallèles par son tracé ,..."
"...il faut donc les tracer obligatoirement par trusquinage,...."
Par définition : Une Torique est une Courbe //les à une Ellipse.... Ou Courbe définie par la Projection du Cercle des Centres des S.Droites du Tore donné... sur l'Intersection de ce Tore par un Plan inclinée et passant par un Diamètre choisi.
Construction par Points certe, mais relativement facile à tracer.... mais surtout qui permet de résoudre la Création des Surfaces Concaves à l'aide d'Outil Spécifique' (Disque de Fraise à Denture demi-circulaire... et non avec une Lame de Scie Circulaire à Denture droite), tout en éliminant la 'fameuse Anomalie de la Surcôte !!'... dans la création des Corniches, par Exemple... Ca doit te rappeler un certain Article sur BLB bois.
"...ce qui est chronophage et peu fiable ! mais on peu s'amuser..."
'Peu fiable'... un peu fort je trouve.....
j'ai remarqué la plupart du temps des erreurs de proche en proche, par exemple quand l'épure échelle 1 est au 1/4 !
C'est plus fiable de faire un ovale et ses points de centres bien définis, surtout si on y place des montages pour défonceuse par exemple !
Apres dans le métier, on vas toujours au pratique et efficacité !
J'aime bien tes démonstrations, qui permettent d'approfondir les réflexions !
Bonsoir sylvain
Je tombe sur ce sujet qui est un super rappel de tout ce qu'on a pu oublier et qui est très complet et je voulais t'en féliciter. Je ne l'avais pas vu mais je ne le lâche plus!!!!
Bravo à toi!
A ce sujet, je suis à la recherche d'un livre de P Ricaud le tracé d'atelier et de géométrie tome 1 ! Je ne le trouve pas en occasion et il est épuisé!
Si quelqu'un du site avait ce livre et voulait s'en débarrasser ca m'intéresse fortement!!
Yann
Bonjour,
Faites une recherche sur
www.rakuten.com avec le titre complet et nom Auteur.
Ou même chose sur Google pour autres Sites.
Attention au prix !
Merci, le fait est je l'ai trouvé et acheté à un prix honnête!
je l'avais déjà fait cette recherche mais je n'avais rien trouvé à moins de 250 euros!
Cordialement
Yann
ebay.fr/itm/12...TAAAOSw0UhhfEd4
Une petite illustration du nombre d'or
C'est vrais qu'il est presque partout !
google.com/sea...041&dpr=0.9
sylvainlefrancomtois Tres bonne synthèse sur le thème Nombre d'Or !!..... et les très Anciens le pratiquaient déjà !... Peut-être savaient observer/comprendre la Nature !!
bonjour,
Quelle mine d'or!!! bravo et un grand merci pour ce partage!!
Je viens de faire un bond de 50 ans en arrière où j'apprenais la géométrie sans que l'on me dise à quoi cela pourrait bien servir , heureusement pour moi, à l'époque, ca me plaisait...et depuis que je menuise, ca me sert!!...et ca prend tout son sens!!
Merci à toi!
de rien, la géométrie est a la base de bien des métiers !
Peux d'anciens savaient lire et écrire, par contre leurs langages géométrique et stéréotomiques, étaient parfaitement maîtrisé !
sylvainlefrancomtois
+1
Merci, merci, merci !
Hey, sylvainlefrancomtois is back
douucement !!!!!
Yes, Sylvain
Nickel ton article !
Se souvenir: moins on mesure moins on se trompe !
Ravi de te retrouver !
Merci Sylvain, heureuse de te relire ici
sylvainlefrancomtois tu appelles ça doucement ?? Un article très bien ficelé avec captures d'écran SketchUp faites maison... Je trouve que c'est très bien comme retour, surtout si tu arrives à réutiliser SketchUp !
Très heureux de te relire !!
Merci pour tous ces partages, ça nous apprend beaucoup, c'est toujours un plaisir. Bon retour.
On retourne sur les banc de l'école... un grand merci pour ces rappels
Ce qui serait pratique, c'est que toutes ces informations se transforment en pdf puis en papier... pour aller à l'atelier
Ca a été discuté ici: