Ce pas à pas présente un projet en cours de réalisation.
Cette année , j'ai été très occupé autour des techniques de constructions en bois, liées au "trait" ou géométrie descriptive appliquée ,pour ceux qui ne connaissent pas le terme .
Dans ce domaine, le dessin d'épures ,permet d'accéder à la maîtrise d'une profession manuelle transformant la matière en objets , dans le bâtiment, ameublement, industrie, etc.(bois,fer,pierre, ect.) ,comme la chaire à prêcher d'illustration ,qui ne peut être fabriquée qui si l'on maîtrise les tracés spécifiques des pièces de bois non connues sur un plan simple.
Ces derniers temps, j'ai été sollicité plusieurs fois notamment, pour de l'aide à donner sur du tracé et des constructions en arêtier .
J'ai déjà produit quelques écrits et informations diverses, mais éparpillées par ci par là ! Donc pour la communauté de l'air du bois ,j'ai décider de faire un pas à pas complet sur l’arêtier pratique et applicable pour tous , depuis les fondamentaux vers des constructions plus complexes et en courbes à intégrer dans des projets .
Je vais essayer de vulgariser au maximum ,et de fournir une progression ludique , ce qui permettra à ceux qui veulent évoluer dans un champ de créations moins limités ,de sortir des plans plats vers de la géométrie dans l'espace !
Liste des articles
- Qu'est ce que l’arêtier ?
- La pyramide
- Exercices de tracés et développements pratiques pyramidaux réguliers
- Exercices de tracés et développements pratiques pyramidaux irréguliers
- Exercices de tracés et développements pratiques pyramidaux tronqués ,pénétrés, et collisions
- Les premières applications d'exercices d'apprentissage d’arêtiers en bois
- Angles de corroyage , arêtes en vraies grandeurs
- Tracés et façonnages d'apprentissage des différents types d'arêtiers droits sur un plan carré
- Tracés et façonnages d'apprentissage des différents types d'arêtiers droits sur un plan rectangle
- Tracés et façonnages d'apprentissage des types d'arêtiers cintrés et courbes depuis un plan carré
- Travaux pratiques d’arêtier : Tréteaux cadet pieds à dévers et pieds avec angle de corroyage
- Le mythique tréteau Buenos Aires !
Qu'est ce que l’arêtier ?
En termes professionnels, l’arêtier désigne une ligne saillante (arête) de rencontre entre deux versants d'un solide (exemple ,deux pans de toiture, deux faces de commode tombeau, trémie à farine, ...).
Arêtier ,nomme aussi la technique de construire des structures aux faces non aplombs et/ou courbes dans deux directions simultanément ,ce qui induit une étude de plans plus élaborés pour avoir des angles et cotes, non connus en géométrie plane (ex: tréteau ou tabouret en arêtier).
On imagine déjà ici, que pour faire ce genre d'ouvrages, un plan simple ne suffit pas ,et que un aventurier sans avoir appris les tracés d'épures en descriptif, va très vite se décourager et revenir à des travaux plus simples avec une certaine frustration! (je suis passé par là aussi) .
Le déclic pour moi, à été d'embaucher moi le menuisier en charpente chez un maître !Ce qui me permis de percevoir concrètement enfin le principe d’arêtier que je n'avais que survolé alors ,et de pouvoir l'apprendre et l'appliquer ou bon me semblait sans limites (charpente, menuiserie, ébénisterie , coffrage ....!)
ici le principe allié avec complexité :
La pyramide
La pyramide est un des solides en arêtier le plus connu universellement depuis l'antiquité, à l'image de celles d’Égypte datées de 4500 ans ou encore plus ancien par plusieurs bois réunis au sommet dans un tipi ! Cette géométrie simple au départ ,permet dès qu'on l'étudie, de dériver ensuite vers les formes les plus improbables que l'on puissent imaginer.
Dans le domaine qui nous intéresse, en changeant la forme de sa base carrée et quatre faces en polygones reguliers et autant de faces ,on arrive à terme au cône de révolution , qui n'est en fait qu'une pyramide avec 360 arêtes !
En changeant son profil d'élévation frontale droit en cintres ou courbes (ce que l'on appelle l'emprunt ou chevron d'emprunt en charpente) ,et suivant une base polygonale on obtient des dômes pyramidaux ,puis à terme des dômes sphériques ,qui ne sont en fait ici aussi' des dômes de pyramides à 360 arêtes cintrées ou courbes !
Enfin on peut imaginer de désaxer la hauteur et/ou faire des bases irrégulières (dévoyées) ou encore plusieurs profils différents d'un versant à l'autre, pour obtenir des pyramides , cônes ,dômes complètement irréguliers, etc .
Le point commun à tous ces solides coniques ,ce sont des arêtes (droites ou courbes) qui relient des versants ,donc l'étude de l’arêtier pour pouvoir ensuite inclure ou combiner ces formes ,tout ou parties dans des ouvrages élaborés sans aucunes limites .
Nota : Le cône classique à emprunt droit se développe facilement , dès que l'emprunt d'un cône est cintré ou courbe les développements sont impossibles, car on arrive aux volumes sphériques et cela créer des "déchirures" !!
Etude de la pyramide classique régulière
La présentation générale de la pyramide régulière est la plus commune. Sa base est un carré et ses quatre faces latérales sont des triangles isocèles (parfois équilatéraux), tous de mêmes dimensions.
C'est pour cela que l'apprentissage de l’arêtier débute par l'étude approfondie de ses composants et de ses propriétés ,puisque toutes autres formes en découleront .Ici nous allons l'aborder en immersion dans le cadre du travail du bois ,donc juste ce qui nous intéresse en pratique !
Nota : En avant propos , nous laisserons de coté la plupart des applications mathématiques "scolaire", car je l'explique ,les anciens ne savaient pas pour la plupart lire et écrire ,et peux pouvaient exécuter des calculs élaborés ! Donc nous allons nous concentrer sur "le trait" proprement dit qui était leur langage commun, c'est à dire construire n'importe quel ouvrage simplement à partir de plans et d'épures tracés avec seulement : quelques mesures, règles, équerres et compas !
La base de la pyramide régulière :
Elle est chaque fois délimitée par un périmètre carré , sa surface est calculée avec la formule simple : coté x coté = aire .
La hauteur de la pyramide régulière :
Elle représente chaque fois la distance entre la base et le sommet (apex). Elle sera toujours à 90° (d'aplomb) depuis l'axe sur l'aire de base . Pour information, aire de base et la hauteur ,servent a calculer le volume de la pyramide : (surface de base x hauteur):3 = volume
Les arêtes de la pyramide régulière :
Elles sont toutes identiques ,elles prennent naissances aux angles de la base et se rejoignent toutes en un point au sommet de la pyramide formant l'apex .
Le sommet ou l'apex de la pyramide régulière :
Il représente chaque fois la réunion des arêtes et des faces latérales en un même point , il situe l'axe de la pyramide car confondu dans la hauteur.
Les faces latérales de la pyramide régulière :
Elles serons chaque fois quatre triangles isocèles (parfois équilatéraux) tous identiques ,ayant comme base un coté du périmètre ,et deux cotés formés par les arêtes de la pyramide ,se joignant au sommet de celle ci .
Les apothèmes de la pyramide régulière :
En géométrie, l'apothème d'un polygone régulier est le rayon du cercle inscrit à ce polygone . Ici dans la pyramide régulière qui nous intéresse en pratique, il représentera l'emprunt (chevron d'emprunt en charpente) ,c'est à dire le profil frontal de la pyramide .
L’apothème de la base avec l'emprunt de la face latérale et la hauteur forment tout trois un triangle d’apothème qui correspond à une demi vue frontale de la pyramide !
L'angle dièdre de la pyramide régulière :
Il représente l'angle formé par deux faces latérales, tout en étant d'équerre à l’arête .C'est très important quand nous voulons apprendre la technique de l’arêtier car il représente l'angle de corroyage chaque fois recherché pour façonner les bois (ex: Pied de tabouret en arêtier)!
Retournons à l'école primaire !
Pour ces prochains chapitres, nous allons devoir nous munir de feuilles de papier, de crayons, gomme ,compas, double décimètre, équerre, et des ciseaux .
Pourquoi ?
Je me suis aperçu avec le temps, que l'immersion directe est parfois compliquée pour certains (personne ne perçois en 3d virtuellement de la même manière des explications ou des exemples) .
Donc nous allons tout d'abord nous familiariser avec des exemples de tracés et de modélisations sans notions d'épaisseurs des matériaux (comme en métallerie ou en zinguerie avec des tôles fines) , ceci pour la simple et bonne raison que des que l'on arrive à former des volumes simplement par leurs faces développées de façons acquises ,ce sera beaucoup plus aisé de rajouter des épaisseurs, angles et autres par la suite .
Pour l'instant ce sera tracés ,découpes et pliages avec les analyses qui vont avec !
Nous allons par ce procédé, commencer par la pyramide régulière , et petit à petit dériver vers des pyramidaux réguliers avec leurs profils en cintres et en courbes ,et enfin dériver le tout en bases ou profils irréguliers !
Pyramide régulière quelconque :
Les deux tracés à découper ci dessous ,représentent ce que l'on à appris à l'école , à savoir de dessiner un carré , et ensuite lui tracer en charnières, 4 triangles identiques, afin que une fois découpé et plié il en résulte une petite pyramide en volume .
Si l'on analyse le résultat , on s"aperçois qu'il y a deux principes principaux de développement d'une pyramide!
1/ par déploiement individuel des quatres face vers le sol depuis l'apex .
2/ par écrasement de l'ensemble vers le sol depuis l'apex .
Ayant tracé arbitrairement quatre triangles identiques quelconques attachés à la base, et après avoir découpé et plié l'ensemble, nous obtenons deux pyramides identiques , mais résulte un inconnue majeure ? La hauteur!
En effet ici c'est la réunion à l'apex des faces qui permet enfin de pouvoir la mesurer !
Dans la pratique , ce qui nous intéresse, c'est d'avoir au départ la mesure de la base ,et la hauteur pyramidale à placer dans un ouvrage!
Donc le cheminement du tracé sera spécifiquement différent par rapport à une pyramide d'écolier, car dans ce cas se sera la longueur des arêtes qui nous sera inconnue ! voilà pourquoi découvrir l’arêtier !
La pyramide régulière cotée :
Ici nous entrons directement dans le vif du sujet, une pyramide à construire avec des mesures à respecter !
1/ Soit une pyramide vue en plan (de dessus) formant une base carrée de 500 mm x 500 mm , et une élévation orthogonale ou vue frontalement d'une hauteur de 500 mm (à retracer à l'échelle que vous désirez) .
Le constat à ce moment ,est que nous pouvons tracer sa base ,sa vue frontale ,mais il est impossible de mesurer la longueur des arêtes ,donc de tracer une face en vraie grandeur de notre projet de pyramide ?? C'est généralement à ce moment là que un novice se rend compte qu'il y a un problème à régler pour construire son projet incluant de l’arêtier!
2/ Pour remédier à cela, on se sert de l' emprunt , soit le coté de la vue frontale de la pyramide sur le dessin ,que nous rabattons au compas par le point de rabattement, vers la ligne de sol (ou de trave chez les charpentiers) .
Puis nous projetons ensuite perpendiculairement vers la vue en plan ce dernier point sur une fuyante horizontale représentant l'alignement au sol de l'emprunt .
A cet instant, nous devinons tout de suite l’intérêt logique de ce premier tracé d’arêtier pratique ! il nous apporte avec un coup de compas ,et un coup d'équerre ,de quoi tracer une face de notre pyramide ,après avoir la mesure en vraie grandeur de nos arêtes !
Nota : Attention dans le dessin ,sur l'élévation frontale de pyramide classique ci dessous ,l'emprunt vu de face est confondu avec la hauteur !!
3/ Au compas , nous traçons un arc de cercle axé depuis le centre de la vue en plan, avec comme écartement le point de l'emprunt en plan généré précédemment , vers toutes les fuyantes d'alignement de tous les emprunts de la construction .
Enfin ,nous n'avons plus qu'à tracer à l'aide de tous ces points générés, les quatres faces triangulaires en vraie grandeur de notre pyramide .
4/ En découpant notre construction , et en repliant le tout en un volume , nous obtenons une pyramide avec la base et sa hauteur désirée !!
Tout le principe approfondis de l’arêtier vers des travaux en courbes les plus complexes, découlerons de ce simple procédé à comprendre au départ, qui par ailleurs porte le nom de développement à la herse en charpente !
L'image n°3 ci dessous ,nous démontre que le procédé reste identique ,quel que soient les mesures !
Exercices de tracés et développements pratiques pyramidaux réguliers
Apres avoir étudié et compris le principe de tracé sur le volume de pyramide classique ,et toujours à l'aide de tracés, découpes et pliages ,nous allons étudier plusieurs cas pratiques d'exercices sur des pyramidaux droits , cintrés ,et courbe .
Un petit peu de terminologie
Dans les écrits qui vont suivre , je vais chaque fois utiliser un vocabulaire spécifique ! Vous en avez déjà eu un échantillon dans le chapitre précédent !
Afin de vous familiariser pour la suite ,voila un petit glossaire qu'il faut essayer d'intégrer ,ce qui vous permettra de visualiser les prochains tracés et explications plus clairement .
La vue en plan : son nom parle pour elle, se sera pour chaque ouvrage à réaliser, le dessin de plan géométrique vu de dessus. Dans l'art du trait , c'est toujours la vue principale que l'on trace en premier ,d'ou partiront des génératrices vers d'autre vues à dessiner ou à développer .
L’élévation orthogonale ou vue de face frontale : Elle représente le profil frontal complet ou partiel d'un ouvrage à réaliser. Elle est destinée à donner toutes les informations de hauteurs et d'emprunt de formes nécessaires aux futurs développements .
Nous reparlerons bien plus tard de l'élévation géométrale pour ne pas vous compliquer les choses à ce stade!
L'emprunt ou chevron d'emprunt : il représente l’apothème d'un pyramidal ou d'un conique,donc le profil frontal de l’arêtier et de la face versant encore inconnus en vraies grandeurs ! Il sert aussi à tracer des épaisseurs de bois à œuvrer ou à reporter (nous le verrons plus tard).
Chez les charpentiers , il se nomme le chevron d'emprunt ,chez les autres professions généralement seulement l'emprunt .
Un développement : C'est une vue pratique d'épure entière ou partielle, déployée en vraie grandeur, issue des autres vues (en plan et élévation). Le développement se dessine par points reliés, générés par les intersections de génératrices projetées en verticales et horizontales .
Un point : C'est l'intersection de deux droites génératrices projetées et/ou arcs de cercles .Les premiers points de constructions et de divisons tracés sont des coordonnées que nous nommons si besoin ,à projeter vers les autres vues et développements .
Un point de rabattement : Il est placé toujours sur la ligne de sol de l'élévation ,à l'intersection avec la ligne de sol projetée depuis la base d'une face de la vue en plan .Il peut selon les cas y avoir d'autres points de rabattements ailleurs ,mais toujours placé à l'intersection de deux traits réciproques depuis deux vues différentes .
Une fuyante : c'est une ligne droite tracée sans mesure particulière .
Un segment : c'est une droite mesurée depuis deux points aux extrémités.
Génératrice : droite ou trait fuyant projeté ou rabattu au compas depuis un point (rabattement) ,dans le but de l'exporter sur d'autres vues en construction . on aura toujours un point défini par une génératrice verticale que coupe perpendiculairement une génératrice horizontale !
La ligne de sol ou de trave : Elle représente le sol virtuel sur lequel est posé l'ouvrage à réaliser. elle est présente chaque fois sur l'élévation comme référence du niveau 0 des hauteurs .Quand une base et plane est de niveau , rien ne doit dépasser en dessous ! Elle sera rabattue en ligne de sol pour le tracé du développement .
En charpente, elle représente le lattis (surface à latter) , soit le dépassement ultime d’arête du dessus de la coupe d'aplomb des chevrons !
Lignes de niveaux : Ce sont les droites horizontales servant généralement à matérialiser et nommer les divisions en élévation et sur un développement .
Liste non exhaustive , ne pas hésiter à faire remonter des intercompréhensions futures .
++++++++++++++
Passons aux développements pratiques sur papiers :
Comme expliqué pour la pyramide régulière à base carrée classique du dernier chapitre ,je vous conseille vivement de faire tous les prochains tracés! En plus c'est amusant d'apprendre ce genre de chose ,et vous en découvrirez par la suite tout l’intérêt ,quand il sera temps de transposer le principe aux bois .
Pyramides à base polygonales régulières
Ci dessous ,trois exemples de pyramides avec des bases polygonales régulières , à savoir triangulaire équilatérale , pentagonale (5 cotés) et hexagonale (6 cotés) !
Que constatons nous ? le principe est complètement similaire à une pyramide à base carrée classique , il faut rabattre chaque fois le chevron d'emprunt vers le développement ,puis tracer les faces individuellement depuis tous les cotés de la vue en plan !
La seule petite complication , est qu'il faut aligner l'élévation frontale perpendiculairement à un emprunt vu en plan! (C'est pour cela que j'ai intentionnellement tracé les polygones de bases vus en plan de façon non aligné avec la feuille de dessin)
Au pliage , on devine ici aussi que la hauteur désirée au départ n'est mesurable que une fois le volume construit .
dômes de pyramides réguliers cintrés et en courbes frontales
Ici nous allons commencer vraiment à utiliser du trait , en effet les développements sur ce types de tracés, impliquent des créations de points .
Analysons la mise en place du dessin d'épure: Que ce soit sur la construction 1 ou 2 , nous avons la même vue en plan ,soit une pyramide en vue de dessus !
Par contre , nous avons deux élévations différentes !
1/ Élévation frontale au profil d'emprunt formé d'un plein cintre : Si nous voulons développer les faces de ce dôme de pyramide , nous devrons les "dérouler à plat" ! Ici c'est aisé de calculer par la formule (PY x D)/4 la longueur de l'emprunt ,ce qui nous facilite la tache avec précision .
2/ Élévation frontale au profil en courbe plus ou moins définie : Si nous voulons développer à plat la face , il va falloir passer par une division segmentaire de celle ci pour déterminer de nouvelles coordonnées utiles ,assez nombreuse pour garder la précision ,mais pas trop pour rester lisible .
Développement d'une face du dôme de pyramide plein cintre :
A/ Sur l’élévation frontale, nous calculons déjà la longueur de l'emprunt , puis nous le divisons en huit segments réguliers par le procédé des cordes . puis par des fuyantes horizontales (lignes de niveaux) , nous projetons toutes ces divisions à l'ensemble du plein cintre .Cette dernière opération, nous donne des nouvelles coordonnées nécessaires à la suite du tracé
B/ Depuis la vue en plan, nous traçons depuis un coté, la longueur développée de l'emprunt .Puis nous le divisons en huit parties égales .
Nota : Pour des constructions à points de coordonnées et génératrices multiples , il faut de préférence tout nommer individuellement par lettres ou chiffres ,car les erreurs peuvent être fréquentes dans des épures très complexes (parfois des milliers de traits)!
C/ Depuis l'élévation ,nous projetons par génératrices, tous les points de coordonnées des deux emprunts formant le plein cintre ,vers la vue en plan sur les divisions réciproques du développement .
Par toutes les intersections représentant les points de coordonnées projetés générés, à l'aide d'un "pistolet de traçage ou perroquet" , nous relions tous les points sur cette construction , et traçons les arêtes développées représentant en miroir ,une face développée en vraie grandeur .
D/ Maintenant que nous avons tracer une des faces développée , il faut tracer les trois autres ! pour cela ,il y à plusieurs solutions !
a/ Par rabattements de tous les points depuis le précédent développement (c'est long ,mais très précis) !
b/ Par gabarit ,en traçant et découpant le développement , puis l'utiliser pour tracer les quatre faces développées sur une autre vue en plan .
Apres avoir découpé la construction complète , nous replions tout en roulant les faces développées en ajustant les arêtes jusqu'à l'apex .
Au final nous obtenons le volumes du dôme de pyramide avec sa hauteur définie .
Développement d'une face du dôme de pyramide en courbe :
A/ Sur l’élévation frontale, nous divisons l'emprunt en huit segments réguliers par le compas cheminant de proche en proche . puis par des fuyantes horizontales , nous projetons toutes ces divisions à l'ensemble de l'élévation .Cette dernière opération, nous donne des nouvelles coordonnées nécessaires à la suite du tracé depuis une courbe .
B/ Depuis la vue en plan, nous traçons depuis un coté, la longueur développée de l'emprunt en reportant autant d'écartements de compas que sur l'emprunt .Puis nous traçons les lignes de divisons . Enfin nous nommons le tout
C/ Depuis l'élévation ,nous projetons par génératrices, tous les points de coordonnées des deux emprunts formant le profil frontal du dôme ,vers la vue en plan sur les divisions réciproques du développement .
Par toutes les intersections représentant les points de coordonnées projetés générés, à l'aide d'un "pistolet de traçage ou perroquet" , nous relions tous les points sur cette construction , et traçons ainsi les arêtes développées représentant en miroir ,une face développée en vraie grandeur .
Nota : J'ai tracé un profil très "pointu", cela pourrait donner quelques imprécisions pratiques ,mais le principe reste juste .
D/ Maintenant que nous avons tracer une des faces développée , il faut tracer les trois autres ! pour cela ,il y à plusieurs solutions comme pour le dôme de pyramide en plein cintre!
a/ Par rabattements de tous les points depuis le précédent développement (c'est long ,mais très précis) !
b/ Par gabarit ,en traçant et découpant le développement , puis l'utiliser pour tracer les quatre faces développées sur une autre vue en plan .
Apres avoir découpé la construction complète , nous replions tout en roulant les faces développées en ajustant les arêtes jusqu'à l'apex .
Au final nous obtenons le volumes du dôme de pyramide avec sa hauteur définie ( en pratique ce sera compliqué d’être à 500 mm) .
Autres pyramidaux cintrés et courbes réguliers :
Pour résumer ce chapitre d'exercices ,Tant que la base polygonale est régulière , et que la hauteur est axée , le principe s'applique chaque fois ,quelques soient les cintrages et courbures d'emprunts .
Tout est possible ! Donc à vous d'en créer d'autres à titre d'entrainement .
Quelques exemples ci dessous .
Nota : Dans nos professions techniques , il est rare de faire plus de faces versants que l'octogone (8 cotés) immergé dans des ouvrages concrets .
A suivre , tracés d'exercices en arêtiers irréguliers !
Exercices de tracés et développements pratiques pyramidaux irréguliers
Dans ce chapitre, nous allons aborder les tracés de pyramidaux irréguliers, c'est à dire quand la base polygonale est irrégulière, ou que l'axe soit déporté, ou encore que les faces versants aient des profils d'emprunts différents!
Tout cela induit donc des versants différents les uns des autres ,qu'il faut relier par des arêtes communes.
Sachant que ces trois critères peuvent être mixés ensembles , les formes les plus improbables sont sans limite ,mais toutes développables!
Découvrons ensembles les trois critères indépendamment !
Pour aborder le sujet et comprendre le principe , le plus simple est de commencer par une pyramide à base rectangulaire !
Pyramide à base rectangulaire
A/ Soit une pyramide à base rectangulaire de 1000 mm x 500 mm, et une hauteur définie 500 mm axée .
Que remarque t'on ?
a/ La vue en plan est rectangle constituée de deux paires de triangles différents axés, de quatre arêtes vues en plan identiques, et de deux paires d'emprunts différents !
b/ L'élévation frontale, représente un triangle isocèle , construit depuis le grand coté de la base sur la hauteur définie !!
c/ La vue de coté frontale, représente un triangle isocèle plus aigu qu'en élévation, construit depuis le petit coté de la base sur la hauteur définie !
Nota: Il faut veiller à tracer l'élévation et la vue de coté assez espacées depuis la vue en plan pour pouvoir installer le développement! Pour ce faire, il suffit d'évaluer l'emprunt.
Sur l'épure nous découvrons donc une vue supplémentaire de coté, ce qui démarquera les tracés futurs par rapport aux tracés de pyramidaux réguliers, là ou une vue en plan et une élévation suffisent !
B/ Après avoir effacé les premiers traits de constructions pour la mise en page, nous construisons le développement .
1/ Nous rabattons les emprunts des deux vues vers la vue en plan . Soit ,les emprunts de l'élévation sur le développement en vraie grandeur de la vue de coté , et les emprunts de la vue de coté sur le développement en vraie grandeur de l'élévation .
2/ D'après cette construction , nous traçons les deux paires de versants en vraies grandeurs .
C/ En découpant la construction , et en repliant le tout , nous obtenons notre volume pyramidal irrégulier et sa hauteur définie mesurable .
Analysons le résultat : Sur l'épure, nous découvrons que chaque fois sur un pyramidal irrégulier rectangulaire, il y aura des faces de versants différents ,donc autant de vues toutes tracées au départ frontalement !
L'emprunt sur l'élévation correspond ici au versant du coté ,et l'emprunt de la vue de coté correspond au versant de l'élévation !
C'est ce qu'il faut retenir de cette première approche ,et qui sera chaque fois le cas dans des pyramidaux irréguliers à base rectangulaire quel que soient les profils d'emprunts .
Pyramide à base quadrilatère quelconque
Continuons avec une pyramide à base quadrilatère quelconque et sa hauteur axée par l'intersection des arêtes vues en plan !
A/ la vue en plan tracée ici, comporte quatre cotés inégaux aussi bien en termes de mesures et d'angles ! L'axe de hauteur de cette pyramide que l'on désire cotée de 500 mm, est centrée sur l'intersection des arêtes vues en plan ,donc l'ensemble induit quatre versants complètement différents 1-2-3-4!
Nous découvrons aussi que les emprunts vus en plan, sont tous indépendant et ne s'alignent pas ,voir même être confondu en plan une arête (n°4) !
B/ En projetant orthogonalement le versant n°1 en élévation frontale, nous remarquons que géométralement le versant n°4 est apparent ,et que l’arête des versant n° 2-3 n'est pas confondue avec l’arête des versants 1-2 !
Si nous élevons les trois autres versants orthogonalement en vues de coté et arrière, nous obtenons ici aussi trois projections géométrales!
Il faut en conclure que les emprunts in situ, ne sont pas mesurables ,puisque ils ne sont pas confondus avec leurs faces versants respectifs .Aie !!
Pour remédier au problème et développer nos faces versants en vraies grandeurs, nous devrons donc passer par les arêtes ou par les emprunts vus en plan ,donc faire de l’arêtier pratique !
Tracé des faces versants par les emprunts en plan :
C/ Depuis la vue en plan, nous projetons quatre constructions perpendiculaires à chacun des emprunts vus en plan !
Celles ci en traçant la hauteur désirée (500 mm) perpendiculairement à chaque emprunts vus en plan (ici projetés plus haut sur une autre ligne de sol ) .
Puis en reliant le point o' de l'apex avec la ligne de sol de chaque construction, nous obtenons les emprunts en vraies grandeurs .
D/ Par rabattements , nous projetons les vraies grandeurs des emprunts par des fuyantes alignant leurs emprunts réciproques en plan . Depuis chaque coté de la base ,en reliant les intersections décrites ci dessus nous pouvons enfin tracer les faces versants développés .
En analysant le résultat , nous découvrons que nous employons le même principe décrit dans le chapitre précédent pour tracer notre développement ! Mais en changeant de plan de projection depuis la vue en plan ,pour avoir les profils d'emprunts en vraies grandeurs à mesurer et rabattre !!
Tracé des faces versants par les arêtes en plan :
Le second procédé passera donc par les arêtes vues en plan ! c'est le grand classique dans le domaine de l’arêtier, car il sert généralement à développer les arêtes afin d'y tracer les bois , assemblages en vraies grandeurs et surtout de tracer l'angle de corroyage ! Mais nous le découvrirons plus tard ,retournons à nos fondamentaux .
E/ Depuis la vue en plan , nous projetons perpendiculairement aux arêtes et l'apex, des points de constructions sur de nouvelles lignes de sol parallèles à ces dernières .
1/ Sur nos constructions, nous traçons la hauteur désirée (500 mm) .
2/ Depuis ces nouveaux points projetés , nous traçons les arêtes en vraies grandeurs.
F/Nous rabattons ensuite toutes les arêtes en vraies grandeurs, vers la vue en plan .
G/ Au compas nous rabattons depuis les points de la base, sur des fuyantes alignant les emprunts vus en plan, toutes les vraies grandeurs d’arêtes !
Ci dessous , j'ai fait le dessin classique par art du trait! En pratique ,nous prenons au compas les écartement de longueur à reporter directement sur le développement .
Puis nous pouvons tracer les faces versants développés .
H/ En découpant la construction , et en repliant le tout , nous obtenons notre volume pyramidal irrégulier et sa hauteur définie mesurable .
En résumé de ce paragraphe , nous découvrons que les élévations et vues frontales ne sont pas utiles ,dès que les bases sont quelconques , seuls les arêtes et emprunts vus en plans sont exploitables .
Pyramides désaxées
Ici nous auront à faire ,à des volumes pyramidaux à base régulière ou l'apex n'est plus placé en axe de sa base !
Nous allons étudier deux cas de figure, à savoir une pyramide sur un plan carré ,et une sur plan hexagonale .
A-B/ Mise en page des épures de pyramides (1) à base carrée et (2) hexagonale :
Sur le tracé orthogonal initial de l'épure (1), soit une base carrée de 500 mmx 500 mm ,avec sa hauteur et apex décalé ,ce qui induit quatre faces versants différents .
L'élévation frontale , se traduit par un triangle quelconque induit par la base et la hauteur 500 mm décalée.
En analysant cette vue, nous apercevons que les emprunts des versants 2 et 4 vus en élévation sont mesurables sans problème car dans une projection parallèle, mais il manque la mesure des deux autres 1 et 3 .
Sur le le tracé orthogonal initial de l'épure (2), soit une base hexagonale de 6 cotés de 300 mm ,avec sa hauteur 500 mm et apex décalé ,ce qui induit six faces versants différents .
L'élévation ici géométrale , se traduit par un profil triangulaire quelconque induit par les faces versants 1 et 6 vus frontalement et la hauteur décalée .
En analysant cette vue, nous apercevons que les emprunts des versants 2 et 5 vus en élévation sont mesurables sans problème car dans une projection parallèle ,le reste pour le moment nous est inconnu .
Pour les deux épures, nous pouvons déjà développer en vraies grandeurs les faces versants par les emprunts vus en élévations, puisque ils sont en projections parallèles !
Développement en vraies grandeurs des autres faces versants (1) à base carrée et (2) hexagonale :
C/ Sur le tracé orthogonal initial de l'épure (1), nous projetons une simple vue frontale de coté , qui nous donne le second profil de cette pyramide avec donc les deux emprunts 1-3 inconnus jusqu'à maintenant !
Enfin de façon classique , nous pouvons développer en vraie grandeur les faces versants 1 et 3 !
D/ Pour la pyramide irrégulière de base hexagonale cela se complexifie un peu !
Sur le tracé orthogonal initial de l'épure (2),en changeant de plan de projection par les emprunts des faces versants 1-4 et 3-6 vus en plan, nous traçons perpendiculairement deux autres élévations géométrales frontales qui nous donnent les longueur d'emprunts 1-4 et 3-6.
**E/* Nous pouvons enfin rabattre ces nouveaux emprunts vus vers le développement, puis tracer les autres faces versants en vraies grandeurs!
Nota: Vous pouvez voir que sur la vue en plan, les emprunts 1 et 4 sont sortis littéralement de leur base respective, en effet l'apex en plan est tellement décalé des cotés de la base qu'il faut ligner celle ci en dehors du dessin pour le tracer perpendiculairement en plan !
F/ En découpant les constructions , et en repliant le tout , nous obtenons nos volumes pyramidaux irréguliers et leurs hauteurs définies mesurables .
En résumé, nous découvrons ici aussi que c'est toujours la même démarche de tracé de développement! Le principe est de toujours rechercher les emprunts inconnus pour pouvoir ensuite les rabattre !
Pyramidaux irréguliers à versants d'emprunts différents
Ici nous commençons vraiment l'immersion complète dans ce que l'art du trait à de plus intéressant ! En effet ,la vue en plan ne peut pas se tracer complètement, car les arêtes communes à deux faces versants d'emprunts aux profils différents ne sont pas jointifs de façon droite mais courbes ! Donc à rechercher !
Pyramide à base carrée avec une face de versant cintré :
Commençons simplement pour expliquer le principe !
A/ Soit une pyramide vue en plan de base carrée de 500 mm x 500 mm sur une hauteur désirée de 500 mm. L’élévation orthogonale principale, est définie frontalement par un profil triangulaire classique. La vue de coté orthogonale est définie par un emprunt droit et un autre en cintre concave.
Analysons la mise en page : On devine ici plusieurs inconnues, hormis les développements à rechercher , les arêtes communes aux faces versants 2-3 et 3-4 ne sont pas connues non plus, car induites par des profils d'emprunts différents!
B/ Nous pouvons d'ors et déjà tracer classiquement le développement de la face versant 1 , et les deux demis faces versants 2 et 4 !
Pour le reste , il faut produire des tracés plus élaborés !
C/ Nous pouvons déjà diviser l'arc de cercle d'emprunt concave en huit par les cordes, puis tracer en fonction de celles ci les divisions horizontales du futur développement ! Nous traçons aussi les lignes de niveaux qui définissent les divisions de la vue de coté,et à l’arête d'emprunt cintré de celle ci nous les rabattons vers la vue en plan .
Nota: Ici j'ai tracé les divisions de l'emprunt cintré avec les cordes au compas , mais j'ai aussi calculé intentionnellement la longueur courbe mathématiquement (à cause des nombreuses questions liées aux différences de mesures des deux méthodes) ! Nous voyons sur le dessin que dans le cas de cette courbes , la différence n'est que de 6/10 de mm ce qui est négligeable dans notre cas ! par contre pour une courbe très arquée dans des grandes épures , le calcul ou la prise de mesures avec un mètre flexible serait préférable !
D/ En rabattant et en projetant les lignes de niveaux depuis la vue de coté vers la face versant 1 déjà développée, puis en les rabattant à nouveau depuis l’arête vers la vue en plan , nous obtenons toutes les intersections réciproques représentant les points à relier pour tracer les arêtes courbes vues en plan !
En ombrant le tout ,nous découvrons la pyramide finie en vue de dessus avec ses faces versants identifiables.
E/ Depuis les arêtes courbes vues en plan ,nous projetons tous les points d'intersections par génératrices sur le développement de la face versant 3. Puis aux intersections avec les lignes de niveaux de divisions ,nous traçons les arêtes courbes, ce qui matérialise la face versant développée .
Nous recommençons l'opération pour la face versant 2 en rabattants les points réciproques depuis l’arête droite déjà développée.
F/ Une vérification peut être faite sur la précision et la justesse des tracés!
En mesurant les cordes des deux développements d’arêtes courbes ,et en les additionnant , ou en cheminant un compas , les deux doivent être évidement de même longueur !
Nota : Comme je l'ai déjà dit , la prise de mesure par les cordes donnent des petites différences , ici elle est de 2/10 de millimétres , autrement dit rien en terme de travaux en bois !
G-H/ Vue complète de la construction de l'épure , et pliage après découpage !
Pyramide à base carrée avec quatre faces de versants différents :
Pour le principe de l'apprentissage, nous compliquerons les choses !
A/ Soit une pyramide irrégulière de base carrée de 500 mm x 500 mm sur une hauteur axée désirée de 500 mm , mais l' élévation et la vue de coté , qui comportent frontalement chaque fois deux profils d'emprunts différents ,donc quatre faces versants différents ,qu'ils faudra relier par des arêtes !
En analysant la mise en place de cette épure , on devine immédiatement le nombre d'inconnues:
Les quatre développements en vraies grandeurs tous différents ,ainsi que les quatre arêtes vues en plan elles aussi toutes différentes ??
B/ Classiquement maintenant, nous divisons et/ou mesurons celles ci .
C/ Nous mettons en place les développements et leurs lignes de divisions des différentes faces versants !
Nota : Si nous traçons ici les lignes de niveaux de chacun des emprunts depuis leurs divisions aux cordes , on s'aperçois que quelque chose n'est pas cohérent ?
En effet si nous voulons pouvoir tracer les arêtes en plan, il faut que chaque points soient sur un même niveau,comme si l'on voulait couper la pyramide "en tranches" !
Ici les niveaux de chaque emprunt ne s’alignent pas avec les autres ? Nous devons trouver une solution précise !!
D/ Nous conservons la mise en page des développements en vraies grandeurs , puis nous effaçons les traits de constructions inutiles .
Pour harmoniser les niveaux de toutes les faces versants, nous divisons la hauteur de la pyramide en huit parties égales ,puis nous projetons tous les points par génératrices et rabattement sur les vue en élévation et de coté. (l'emprunt droit de la vue de coté ,correspond déjà à ces divisions dans notre projet) .
En analysant cette construction, nous devinons la logique que tous les points qui seront projetés verticalement de chaque emprunt ,seront réciproques d'altitudes respectives, quelques soient leurs profils ,ayant des lignes de niveaux communes !
E/ Classiquement maintenant,nous projetons les nouveaux points de divisions sur les différents développement, puis nous traçons les différentes courbes aux intersections de tous les développement et les courbes d’arêtes en plan . Si nous mesurons les courbes par les cordes , nous devinons quelles sont pratiquement identiques avec une variation infime sans incidence de façonnage de quelques 1/10 de millimètres !
En résumé, toutes les surfaces courbes différentes développées à plat, une fois repliées ,se joindront parfaitement aux arêtes en courbes !
G-H/ Vue complète de la construction de l'épure , et pliage après découpage !
A suivre
Exercices de tracés et développements pratiques pyramidaux tronqués ,pénétrés, et collisions
Nous abordons le dernier chapitre d’exercices et tracés pyramidaux sur papier à découper !
Au départ les termes employés de troncs, pénétrations, collisions, prêtent un peu à sourire, et les gens dans une classe généralement, se regardent bêtement avant d'identifier ce dont il est question (rires)!
Mais ces sont principes très importants pour se familiariser avec des éléments étrangers projetés ou découpés sur un volume de pyramide, et qui permettront plus tard de tracer des projets en bois !
Trois grands principes changent ou altèrent une pyramides :
1/ Les troncs de pyramides : Ce sont tous les actes de sectionnement d'une partie de la pyramide par un plan de coupe ,placé sur sa hauteur d’origine. Ils peuvent être de sections horizontales ,biaises , à l'apex et/ou à la base, et parallèle ou non à cette dernière .
Dans des travaux de bois d’arêtiers, se seraient par exemples: L'assise d'un tabouret, une vitrine biaise , ou en charpente une toiture sur des murs en faux niveaux . Ils occasionneront des accidents qu'ils faut identifier et savoir tracer sur une épure de fabrication !
2/ Les pénétrations de pyramides : Ce sont tous les éléments en volumes étrangers qui traverseraient les faces versants d'une pyramide (de niveau, d'aplomb, obliquement) ! Ils occasionnent des vides sur les surfaces de versants , donc des éléments de raccordement à tracer sur une épure de fabrication . Par exemples: Des fenêtres ou lucarnes de toitures, des cheminées , le vide de la face frontale d'un tabouret entre les montants et traverses, etc .
3/ Les collisions de pyramides : Ce sont tous les volumes étrangers solides, qui viennent s'encastrer depuis un même plan dans une pyramide déformant ainsi sa géométrie globale !
Ils produiront eux aussi des raccordements à rechercher . Par exemples : Le mur d'une tour ronde encastrée dans une toiture en charpente ("noues"), Des pieds de mobiliers pyramidaux en ébénisterie ou encore un habillage de hotte de cheminée sur un mur biais ou rond en menuiserie , etc etc ..
Tracés des troncs de pyramides
Le tronc de pyramide horizontal (de niveau) :
C'est le plus commun pour visualiser, et en fait aussi le plus utilisé dans des travaux en bois ,c'est le tronc pyramidal en section horizontale du plan de coupe (dit "de niveau" dans le métier) !
A l'image d'un tabouret ou d'un tréteau ,c'est une pyramide classique de plan carré ou irrégulière sur plan polygonal dont on à sectionné une partie de l'apex ,laissant une surface plane parallèle à la vue en plan!
A/ Le tracé de mise en page d'épure est assez simple, ce sont des pyramidaux classiques comme ceux étudiés du début de ce pas à pas ,mais sur lesquels, nous devrons tracer en plus des sections de troncs désirés.
Soit une pyramide régulière à base carrée de 500 mm x 500 mm tronquée sur sa hauteur à 250 mm, et une pyramide irrégulière à base rectangulaire de 1000 mm x 500 mm ,tronquée sur sa hauteur à 250 mm .
B/ Le principe du rabattement pour tracer les développements en vraies grandeurs reste classique ,sauf qu'ici ce seront les emprunts traversés par le plan de coupe, qui créeront les points correspondant au niveau de la section de tronc désirée, vers l'apex, que l'on rabattra à plat .
C/ Les épures complètes des deux constructions, comportent ici tous les rabattements nécessaires et développements en vraies grandeurs des faces versants , avec en plus le tracé par rabattements de la surface plane des sections du troncs de chaque construction .
D/Le pliage après découpage, ici aussi nous permet de mesurer la hauteur désirée de la section .
En analysant les dessins nous découvrons que le principe est toujours le même depuis le début de cet apprentissage sauf que les accidents ajoutent des nouveaux points de coordonnées à projeter .
E/ Dans les exemples ci dessous de troncs pyramidaux avec sections horizontales ,quelques soient les contours de la base (de niveau), de hauteurs désaxées et/ou profils d'emprunt différent du pyramidal initial, représenteront toujours une surface plane parallèle à la vue en plan!
En résumé, tous les points d'une section de tronc pyramidal horizontale ,se trouvent confondus sur une même ligne de niveau commune à l'élévation et vue de coté .
Le tronc de pyramide biais parallèle au plan de coupe :
Ici l'exercice se complexifie, car les points de projections de la sections du plan de coupe, ne seront plus confondus sur un même niveau !
A/ Le tracé de mise en page d'épure ,reste ici classique, sauf que les sections de troncs sont placés en biais non parallèles à la ligne de sol des élévations et/ou sections frontales vue de coté géométralement, définies par un plan de coupe oblique !
Soit une pyramide régulière à base carrée de 500 mm x 500 mm tronquée avec section biaise vue en profil oblique de coté sur l'élévation , et une pyramide irrégulière à base rectangulaire de 1000 mm x 500 mm ,elle aussi avec section biaise vue en profil oblique sur élévation, et vue frontalement sur la vue de coté .
En analysant la mise en page d'épures , nous allons découvrir l'importance des emprunts pour toute la suite de ce pas à pas !
En effet ce sont eux qui nous apporteront toutes les informations nécessaires aux futurs tracés de développements et autres .
Les emprunts 2-4 de l'élévation sectionnés par le plan de coupe , nous donnent deux mesures différentes à projeter par rabattements.
Les emprunts 1-3 de la vue de coté, nous donnent deux mesures identiques, mais avec deux points supplémentaires à projeter par rabattements.
C'est maintenant que dans l'apprentissage de l’arêtier que l'on apprend que l'emprunt (ou chevron d'emprunt chez les charpentier) ,servira à tracer puis projeter toutes les informations d'un ouvrage à exécuter en bois (sections de traverses, arasements , longueur de panneaux ,coupes de chevrons, épaisseurs de bois ,etc etc ..) Mais nous y reviendrons plus tard) !
B/ Les rabattements des différents emprunts se font classiquement , sauf que pour les emprunts 1-3 placés sur la vue de coté ,les rabattements projettent chacun deux points (a-d et b-c)!
C'est donc ici qu'il faut véritablement commencer à nommer les éléments étrangers rapportés sur un pyramidal! Donc les points de coordonnées de la surface biaise du tronc sera identifiée par des lettres ou des chiffres (ici a-b-c-d) .
C/ Pour tracer ensuite toutes les faces versants en vraies grandeurs, il nous suffit de projeter part génératrices fuyantes, les points a-b-c-d de la section de tronc vue en plan parallèlement, vers leurs réciproques en a'-b'-c'-d' des rabattements d'emprunts exécutés précédemment .
Aux intersections , par des droites nous pouvons tracer les faces versants développées avec chacune leur coupe de tronc en vraie grandeur .
D/ Pour développer la section du tronc pyramidal en vraie grandeur, Le principe reste identique, sauf qu'ici nous ne rabattons vers le développement que les points de coordonnées de celui ci ! (en violet sur le dessin).
E/Le pliage en volume après découpage, nous permet de mesurer les altitudes désirées de la section de tronc pyramidal .
Le tronc de pyramide régulier biais non parallèle au plan de coupe :
Quand une pyramide n'est plus parallèle depuis sa base à un plan de coupe oblique, la section de tronc se trouve "déformée" , induisant quatre faces versants différents en orthogonal.
Donc il est impossible de tracer orthogonalement la vue en plan complète avec la section, ni l'élévation et les vues de cotés , puisque nous ne connaissons aucunes altitudes mesurables au départ ??
A/ Commençons la mise en page de l'épure avec les données connues !
Soit une pyramide à base carrée de 500 mm x 500 mm et de 500 mm de hauteur, placée sous un plan de coupe oblique la sectionnant en tronc, mais sachant que sa base se situe non parallèle à celui ci (45° pour l'exercice) !
Nota : Il apparaît que les cotés de l’élévation géométrale représentes ici les arêtes de la pyramide entière en vraie grandeur, en effet cette vue étant générée par sa position à 45° de vue en plan, donc les arêtes vues en plan sont vues parallèlement et perpendiculairement au plan de coupe .
B/ Nous devons déjà tracer cette section sur la vue en plan, puis la nommer par quatre points singulier .
a: Depuis la vue en plan, nous projetons vers l'élévation les emprunts (2-3, 1-4 ici confondus ) , ce qui les positionnent géométralement entiers depuis l'apex, mais sectionnés par le plan de coupe oblique .
b: Depuis les points générés par cette construction, nous projetons maintenant ceux ci vers la vue en plan.
c: Aux intersections des génératrices réciproques des emprunts vus en plan, se trouvent les nouveaux points de coordonnées pour tracer la section biaise vue de dessus, puis nous la nommons ici a-b-c-d .
C/ En rabattant l’arête en vraie grandeur depuis l'élévation, et en la projetant vers la vue en plan, nous pouvons tracer classiquement dans un premier temps, les développements des quatre faces versants entiers en vraies grandeurs .
D-E/ En projetant les points a-b-c-d depuis les emprunts vus géométralement en élévation sur les arêtes, puis en rabattants et projetant ces nouveaux points vers le développement (tracés violet sur le dessin) ,nous obtenons les points de coordonnées développés en vraies grandeurs, des traits de coupes de chaque face versant .
Nota : Il est possible aussi depuis la section vue en plan, de projeter les points a-b-c-d perpendiculairement sur les arêtes déjà développées entières , mais dans la réalité le résultat sera moins précis aux intersections, et le principe doit servir uniquement de vérification.
Enfin depuis les faces versants développées à plat , nous pouvons projeter les points de coordonnées b'-c' (tracés bleu sur le dessin), qui nous permettent de tracer la section et sa surface en vraie grandeur .
F/Le pliage en volume après découpage, nous permet de mesurer les altitudes de la section de tronc pyramidal .
En résumé, le fait que la base de la pyramide est été placé à 45° par rapport au plan de coupe, nous donne une construction symétrique, mais nous permet d'assimiler le principe !
Dans l'exemple suivant ,nous allons l'appliquer sur une pyramide irrégulière à base rectangulaire, placée de manière aléatoire par rapport à son plan de coupe .
Le tronc de pyramide irrégulier biais non parallèle au plan de coupe :
A/ La mise en page de l'épure reste classique, soit une vue en plan de 1000 mm x 500 mm placée aléatoirement par rapport au plan de coupe, et une élévation géométrale représentant cette pyramide entière de hauteur 500 mm ,sectionnée par le plan de coupe !
B/ La section tracée vue en plan est définie par les emprunts et arêtes vus en plan projetés entiers vers l'élévation, puis une fois sectionnés par le plan de coupe, cette construction crée les coordonnées de points a-b-c-d, à projeter vers la vue en plan .
C/ Nous devons maintenant tracer le développement des faces versants en vraies grandeurs ! Contrairement au paragraphe précédent de la pyramide à 45°, dont on connaissait la longueur des arêtes dues à sa position ,ici nous devons la rechercher afin de pouvoir finaliser les tracés entiers .
Nous procéderons par un développement d’arête depuis la vue en plan, afin de pouvoir ensuite la projeter à chacune des faces versants .
A partir d'une arête vue en plan ,et en y traçant perpendiculairement la hauteur de la pyramide 500 mm, nous traçons aux extrémités de la construction l’hypoténuse représentant l’arête en vraie grandeur (en violet sur le dessin), puis projetée par rabattements simultanés vers les autres développements pour tracer toutes les faces versants .
D/ Le tracé complet de chaque face versant développé avec leur section respective, se produit à l'aide de la projection d'une arête vue en plan projetée par rabattement vers l'élévation (en violet sur le dessin), puis en y traçant la hauteur de la pyramide, nous traçons le profil de l’arête en vraie grandeur.
Sur cette nouvelle construction, nous projetons horizontalement les points de section de tronc, ce qui nous donne les mesures des arêtes sectionnées à reporter avec l’écartement de compas vers le développement .
A l'aide des mesures, nos traçons les faces versants et leurs lignes de coupes en vraies grandeurs, puis nous pouvons vérifier le bien fondé des tracés en projetant les points de sections vus en plan, perpendiculairement à la base vers les faces versants développés !
Enfin, avec les longueurs des sections de chaque faces versants développés , nous pouvons tracer la surface de la section de tronc en vraie grandeur .
C/ Le pliage en volume après découpage, nous permet de mesurer les altitudes de la section de tronc pyramidal .
Les troncs de pyramides biais à plan de coupe depuis la base :
Ici, les troncs sont effectués par un plan de coupe s'articulant depuis la base des pyramidaux, le principe appliqué reste strictement le même que les derniers chapitres, sauf que ce sont des faces versants à rechercher cette fois tracés depuis la section vue en plan à rechercher elle aussi en vraie grandeur !
A/ La mise en page de l'épure, nous donne ici des vues en plan et des élévations classiques, avec leurs plans de coupes!
Sauf que les sections rabattues en plan ne sont pas exploitables car projetées biaises depuis les élévation ?
B-C/ La projection en vraie grandeur des sections de troncs, se produit par un rabattement de leurs points issus du plan de coupe depuis l'élévation sur la ligne de sol, puis projetés ensuite vers la vue en plan .
Les arêtes ou emprunts réciproques sur les vues en plan, doivent être eux aussi projetés en horizontal ,pour avoir les points d'intersections de constructions, enfin nous pouvons tracer les sections de troncs vues en plan et en vraies grandeurs (voir l'agrandissement) .
D/ Les tracés de constructions complètes, se produisent classiquement, mais rabattus cette fois sur les sections de troncs en vraies grandeurs vues en plan !
E/ Le pliage en volume après découpage, nous permet de mesurer les altitudes de la section de tronc pyramidal .
Les pénétrations dans une pyramide
Ce sont tous corps étrangers venant traverser des faces versants de pyramidaux, dont il faut rechercher les vides occasionnés en vraies grandeurs sur une ou plusieurs faces versants !
ici les fondamentaux se classifient généralement par :
1/ Pénétrations verticales, à l'image d'une cheminée de toiture .
2/ Pénétration horizontale (de niveau), comme des lucarnes en toitures .
3/ Pénétration oblique, comme des fenêtres de toits (velux) décalées .
Tracés d'apprentissage de pénétrations sur des pyramides :
A/ La mise en page de l'épure reste classique, mais en plus li faut tracer les éléments pénétrants sur les vues en plan et élévations !
Sur le dessin d'exemples, j'ai ajouté les vues de cotés pour une lecture plus détaillée, on y découvre facilement les trois grands principes .
B/ Apres avoir développés les faces versant depuis la vue en plan, nous projetons les éléments de vides laissés par les pénétrants étrangers aux pyramides .
La technique est de rabattre et projeter les points des pénétrations vers la vue en plan, et de faire intersections avec les points réciproques des pénétrations projetés venant de celle ci .
Aux intersections , nous pouvons tracer les vides exacts à exécuter sur les faces versants .
C/ Le pliage en volume après découpage, nous permet de découvrir les vides parfaitement découpés et orientés des pénétrations désirées !
Tracés de pénétrations circulaires sur des pyramides :
Ici, nous allons visualiser les techniques de base des pénétrations circulaires de pyramidaux, c'est à dire que les éléments étrangers sont de formes cylindriques, pénétrant verticalement et/ou horizontalement une ou des faces versants de pyramides .
A/ La mise en page de l'épure reste classique, mais en plus il faut tracer les éléments pénétrants de formes circulaires sur les vues en plan et élévations !
Les deux exemples représentent ce qui pourrait être une cheminée ou un pied de mobilier en pénétration verticale, et ce qui serait un élément design depuis la base en horizontal .
En analysant la mise en page de l'épure, nous découvrons que la pénétration verticale d'aplomb est assez simple à dessiner, et que la seule inconnue reste le vide de celle ci sur sa face versant développée .
Pour la pénétration horizontale, deux inconnues : Sur le développement des faces versants ainsi que sur la vue en plan ?
Tracé de la pénétration verticale cylindrique :
1/ Commençons par la pénétration verticale d'aplomb , la technique est simple! Il s'agit de diviser dans un premier temps le profil de celle ci vue en plan par les cordes en parties égales en 16 segments (8 serait insuffisant pour un si petit diamètre).
Puis de projeter ces nouveaux points de coordonnées vers l'emprunt d'élévation et le développement.
2/ Puis nous rabattons les points de coordonnées projetés sur l'emprunt d' élévation, vers la ligne de sol , et enfin nous les projetons vers le développement.
3/ Aux intersections des génératrices, de la face versant développé, nous traçons la courbe du vide de pénétration circulaire en vraie grandeur (ellipse) .
Tracé de la pénétration horizontale cylindrique :
1/ Pour la pénétration horizontale de niveau , la technique est similaire ! Il s'agit de diviser dans un premier temps le profil de celle ci vue en élévation cette fois ci , par les cordes en parties égales en 8 segments (Ici ce sera suffisant) .
Projetons ces nouveaux points de coordonnées vers l'emprunt et rabattons les vers le développement ,et enfin nous les projetons aussi vers la vue en plan .
2/ Puis nous rabattons ces points de coordonnées projetés vers le développement des faces impliquées. Nous projetons aussi les points donnés sur les arêtes développées, vers la vue en plan .
3/ Aux intersections des génératrices, des faces versants développés, nous traçons la courbe du vide de pénétration circulaire en vraie grandeur (elliptique) , et aux intersections des génératrices sur la vue en plan, nous pouvons enfin tracer la pénétration vue en plan avec son vrais profil vu de dessus (elliptique).
B/ Le dessin d'épure complet, nous donne les deux volumes de pyramides avec leurs vides de pénétrations en lieu et place à découper aussi .
C/ Le pliage des volumes après découpage, nous permet de découvrir les vides courbes parfaitement découpés et orientés des pénétrations désirées !
Différence de choix en tracés de pénétrations sur des pyramidaux :
Plus haut nous avons parlé des principes généraux des pénétrations sur des pyramides, toutefois en menuiserie ou en ébénisterie, souvent un choix s'impose !
En effet nous pouvons décider de pénétrer un pyramidal horizontalement ou perpendiculairement pour un même rendu global .
Je m'explique ! Dans la pratique, l'exemple ci dessous pourrait représenter un "marchepied" constitué d'un tronc de pyramide avec des vides sur les quatre faces versants, parallèle aux arêtes et la base .
Nota : Je rappelle ici que nous ne travaillons encore que sur les développements de surfaces volumétriques sans notions d'épaisseurs de matières (ex tôle métallique ou feuille de papier à découper et replier)!
A/ La mise en page des épures ici, nous illustrent deux pyramidaux tronconiques identiques dans leurs mesures et contours, soit une base de 500 mm x 500 mm sur une hauteur entière de 500 mm sectionnée à 250 mm .
a: Le premier concept (à gauche) représente la surface d'un marchepied, avec pénétrations horizontales parallèles à la base!
Nous remarquons que celles ci vues sur l'élévation et la vue de coté sont identiques, et tracées arbitrairement montants et traverses à 50 mm du profil global. Les projections possibles sur la vue en plan, nous définissent déjà le troncs global ainsi que les traverses vues de dessus, mais il nous manque la vue complète des vides de pénétrations .
b: Le second concept (à droite) représente la même surface du marchepied, mais avec pénétrations obliques perpendiculaires aux l'emprunts des faces versants. Ici les mesures désirées sont tracées depuis les emprunts, puis alignées en traverses sur l'élévation et la vue de coté !
Les projections possibles en plan, nous donnent des traverses en vue de dessus, complètement différentes au premier concept ? Et il nous manque ici aussi la vue complète des vides de pénétrations ?
Tracé d'épure du projet avec pénétration horizontale arbitraire :
1/ Le tracé de la vue en plan complète, se produit grâce à tous les points projetés depuis l'élévation vers les arêtes vues en plan. En ajoutant des couleurs , nous matérialisons géométralement le projet.
2/ La mise en place du développement se fait classiquement depuis les points projetés depuis l’emprunt d'élévation vers la vue en plan .
3/ Le tracé complet du développement, se produit classiquement en projetant tous les points de coordonnées secondaires projetés depuis l'emprunt d'élévation ,vers le développement . puis on trace la surface de la section de tronc . Enfin par des couleurs nous matérialisons l'ensemble .
Ici l'analyse est très intéressante , car si nous avons une élévation et une vue en plan qui nous paraissent équilibrées , nous découvrons sur les faces versants développés en vraies grandeurs, des cotes complètement différentes entre les montants et les traverses ??
De plus comme nous le découvrirons plus tard en travaillant sur des épures pratiques de constructions en bois, que les vides laissés par les pénétrations horizontales parallèles tracées arbitrairement depuis l'élévation, donneront des arasements obliques mais en plus biais sur les assemblages !
Pour remédier à cela, nous opterons de préférence pour des pénétrations perpendiculaire à l'emprunt d'élévation !
Tracé d'épure du projet avec pénétration perpendiculaire à l'emprunt :
1/ Le tracé primaire ici se produit par les mesures de traverses effectuées cette fois sur l'emprunt d'élévation, puis rabattus et projetés vers le développement d'une face versant .
Cette première opération nous permet de tracer la surface désirée du projet avec des mesures voulues des éléments vus en vraies grandeurs, afin de pouvoir les projeter ensuite vers les autres vues .
Les montants sont tracés sur le développement, et auront de fait la même largeur que les traverses.
Nota : C'est ici que l'on devine toute l'importance de savoir développer, car dans des projets futur, cela permet de dessiner toutes les informations de l'ouvrage fini (largeur de bois , moulures, panneaux, médaillons, cintres , etc , en vraies grandeur!) En effet le tracé arbitraire sur l'élévation crée des déformations parfois très inesthétiques en vraie grandeur !
Ex : Imaginons une marqueterie en damier dessinée directement sur l'élévation ? Une fois développée en vraie grandeur celle ci serait informe !
2/ Le tracé de la vue en plan, se produit donc dans notre cas, par les intersections des génératrices projetées depuis l'élévation et le développement . Enfin par des couleurs nous matérialisons géométralement l'ensemble .
3/ Le tracé de l'élévation, se produit cette fois ci en projetant les points de coordonnées depuis la vue en plan !
Enfin nous pouvons finaliser le tracé d'épure complet pour le découpage, en traçant les autres faces versants.
B/ L’analyse des deux tracés finaux ci dessous , présentent généralement pour un novice peux de différences! Mais ces différences permettent immédiatement à un initié aux techniques d’arêtiers de savoir si un ouvrage sera réussi ou pas!
En résumé , Un tracé d'épure pénétrant horizontal gagnera du temps pour un objet fonctionnel sans intérêt décoratif , et un tracé d'épure pénétrant perpendiculairement aux versants , permet de développer en vraie grandeur les éléments de constructions, mais aussi des assemblages à petit cadre (tennonage ,mortaisage, rainurage, mouluration, etc) sur des champs d’équerres , donc de travailler classiquement à la main ou aux machines ! Mais nous en reparlerons plus tard !
C/ Le pliage des volumes après découpage, nous permet de découvrir les vides parfaitement découpés et orientés des pénétrations des deux principes et visualiser les différences !
Collisions contre des pyramides
Une collision de pyramide, implique l'interaction d'un autre solide étranger la percutant ,et "s'encastrant" dans une partie de sa géométrie originelle, occasionnant des raccordements à rechercher par épures dans le domaine des tracés d’arêtiers .
A/ La mise en page du tracé d'épures d'apprentissage, ici nous illustre des pyramides classique à bases carrées 500 mm x 500 mm , sur une hauteur de 500 mm .
On devine en couleurs les collisions par un parallélépipède, une autre pyramide, et un cylindre , eux aussi dessinés en plan et en élévation .
B/ La perspective de l'ensemble des pyramides reconstituées, nous montre par transparence les collisions avec les autres volumes étrangers, et nous matérialise bien les raccordements que l'on doit pouvoir identifier et tracer.
Le principe de tracer des raccordements de collision reste assez simple, et est utilisé majoritairement en charpente ! Mais dans des créations de menuiserie ou ébénisterie, la pratique peut être très utile à des création design !
Collision de pyramide par un parallélépipède :
L'exercice ici permet immédiatement de découvrir le principe ! A la base c'est une épure de pyramide classique sur laquelle on ajoute l'éléments étranger qui percute celle ci à un endroit désiré . (Imaginons une hotte posée sur l'angle d'un mur).
Maintenant que nous somme rompus aux exercices de tracés, nous apercevons sur l'épure que c'est encore et toujours l'emprunt qui nous défini les points de coordonnées à rabattre et projeter vers le développement .
Le pliage du volume après découpage, nous permet de découvrir les mesures le raccordement exact de contact avec l'élément étranger !
Collision de pyramide par une autre pyramide :
A part étudier l'épure , il n'y a pas grand chose à dire , sinon que la généralité de ce tracé ne diffère pas d'une collision avec un parallélépipède !
En effet ,tant que les volumes qui s'entrechoquent sont issus de profils droit, ils produisent généralement peu de points de cordonnées à projeter !
Collision de pyramide par un cylindre :
Nous connaissons tous le principe de la tour ronde encastrée dans un angle de mur, ici le principe vu plus haut s'applique à l'identique, sauf que nous sommes cette fois dans de la courbe pour les raccordements (appelée une noue chez les charpentier), et il faut créer des points de coordonnées supplémentaires, afin de les modéliser à l'épure.
a: Nous traçons classiquement la mise en page de l'épure, puis nous y plaçons la collision sur la vue en plan et l'élévation !
b: Sur l'élévation, nous divisons en parties égales (ici quatre niveaux ) la hauteur du raccord de collision, puis nous projetons ces divisions de niveaux vers la vue en plan et le développement .
c: Ces dernières projetées sur l'arc de cercle de la collision vue en plan, nous donnent les points de cordonnées à projeter vers le développement et l'élévation .
d: Aux intersections réciproques , nous pouvons tracer les courbes, vue en élévation et en vraies grandeurs sur le développement .
Le pliage du volume après découpage, nous permet de découvrir le raccordement courbe exact de contact avec le cylindre étranger !
Voilà pour ce long chapitre , Il faut garder à l'esprit que les principes de bases décrits ici , s'appliquent à n'importe quel pyramidal de toutes formes et accidenté de toutes les manières, il n'y a pas de limites.
Evidemment plus les volumes et leurs accidents sont complexes , plus les tracés d'épures se compliqueront à cause de la multiplication des points de coordonnées !
ici une application pratique sur l'air du bois
Les premières applications d'exercices d'apprentissage d’arêtiers en bois
Notions d'épaisseurs en arêtier
A partir de maintenant, nous allons découvrir des exercices à façonner en bois depuis des épures d'apprentissages classiques !
Celles ci comporteront généralement moins de vues tracées, car en pratique nous ne traçons que l’essentiel utile de fabrication.
Dans ce chapitre, nous travaillerons sur des panneaux de bois de 22 mm (cp, medium, ...), comme cela nous resterons encore dans la logique des développements et des tracés issus des chapitres précédents d'exercices sur papier .
Nota : Je prend souvent les mêmes cotes pour mes exemples, évidement vous tracez avec les cotes que vous voulez, mais toutefois ne descendez pas en dessous de 30 cm ,c'est plus facile d’être précis et moins dangereux que des pièces trop petites !
Tracé et exécution d'une pyramide régulière en panneau de 22 mm :
A/ Le tracé de l'épure avec épaisseur de bois se produit classiquement au départ, par les contours "hors tout" désirés, de la vue en plan et d’élévation, puis d'un développement !
Ici un seul développement suffit car toutes les faces versants seront identiques à usiner !
Sur cette mise en page , nous traçons sur les emprunts d'élévation et la base, l'épaisseur désirée de bois (ici en 22 mm).
En définitive, nous traçons une coupe perpendiculaire complète de la pyramide par les emprunts ,placée en calque sur l'élévation globale !
B/ Le tracé complet de l'épure de fabrication, se complique un peu par rapport au développé simple d'une face versant !
Le mot clef est rigueur et précision, car c'est le tracé final qui permet de prendre toutes les mesures et angles de façonnage .
a: En premier lieu, nous traçons la vue en plan complète, en y projetant les points d'intersections par génératrices depuis l'élévation.
En traçant perpendiculairement à la vue en plan l'épaisseur de panneau de fabrication, nous pouvons avoir la section "vue par bout" (terme employé en charpente généralement) de la base avec ses vraies mesures et angles précis à transcrire sur la pièce de bois à façonner.
b: Depuis l'emprunt en élévation, nous rabattons vers la ligne de sol tout les points nécessaires, puis nous les projetons vers le développement.
Ici sur les agrandissements, nous découvrons le procédé. Tous les points induit par le tracé de l'épaisseur du bois ,doivent être projetés perpendiculairement sur l'emprunt, avant d’être rabattus pour être alignés correctement avec le point de rabattement .
Sur l'agrandissement n°1, j'ai rabattu le point de coupe de deux manières depuis le point de rabattement pour illustrer le fait qu'il soit indispensable de projeter perpendiculairement les points sur l'emprunt avant de rabattre et projeter. On devine bien ici que projeter directement le point amène à une erreur !
Sur l'agrandissement n°2, j'ai illustré le rabattement en modélisant l'emprunt complet avec épaisseur et coupes pour définir visuellement le principe .
C/ L'épure pratique de fabrication complète ci dessous , nous permet d'avoir toutes les mesures et angles à retranscrire sur les bois , puis de les façonner!
Sur le développement de la face versant, en traçant perpendiculairement à l’arête et la pente de coupe vue de dessus , l'épaisseur de 22 mm de nos panneaux , aux intersections nous traçons l'angle de coupe vu en vraie grandeur et angle.
D/ Apres avoir tracés les bois depuis l'épure et le façonnage et ajustage ,nous montons la pyramide désirée en un volume fini !
Ici des exemples présent sur l'air du bois : lairdubois.fr/..._comment_167702
lairdubois.fr/..._comment_346931
Les deux prochains exercices , découlent directement de ce premier tracé, cela vous permet de compliquer à mesure votre apprentissage tout en s'appuyant chaque fois sur une visualisation globale acquise de progression étape par étape pour des projet en bois ,comme pour les exercices en papiers précédent !
Tracé et exécution d'un tronc de pyramide régulière en panneau de 22 mm :
Nous reprenons donc l'épure précédente, sur laquelle nous ajoutons une section de tronc .Cette opération modifie les faces versants, et ajoute une pièce en plateau de niveau.
A/ Sur l'épure globale, nous ajoutons ces nouveaux éléments : Une section de tronc vue en élévation de hauteur 266 mm , puis par projection de génératrices, nous traçons la vue en plan avec le tronc complet vu de dessus .
L'ensemble de ses nouveaux points, nous permet de tracer le développement de la face versant en vraie grandeur classiquement .
B/ L'épure pratique de fabrication complète ci dessous, nous permet d'avoir toutes les mesures et angles à retranscrire sur les bois, puis de les façonner!
C/ Ici aussi, après avoir tracés les bois depuis l'épure et le façonnage et ajustage ,nous montons la pyramide désirée en un volume fini !
Tracé et exécution d'un tronc de pyramide régulière en panneau de 22 mm avec pénétration perpendiculaire :
Afin d'appliquer toute les techniques de bases, nous procédons au tracé depuis l'épure précédente, d'une pénétration perpendiculaire aux faces versants !
Cet exercice nous familiarisera un peu plus avec la logique petit cadre traditionnel à transposer en arêtier .
A/ Nous commençons par tracer sur l'emprunt d'élévation, les sections de traverses que nous désirons, ici 80 mm en parement, puis nous les rabattons et projetons vers le développement de la face versant en vraie grandeur.
B/ Nous traçons les traverses sur la face versant développée, puis nous y traçons les montants désirés (ici largeur 80 mm en parement .
C/ Nous traçons et matérialisons le développement complet en vraie grandeur de la face versant, puis en projetant ces nouveaux points depuis le développement vers la vue en plan, nous pouvons tracer cette dernière complètement.
D/ En projetant les nouveaux points depuis la vue en plan vers l'élévation, nous pouvons tracer cette dernière complètement !
Ci dessous, la vue entière de l'épure d'exercice, et modélisation du tracé et d’exécution des panneaux de l’ouvrage !
Ci dessous un bel exercice d'épure et d'exécution à faire, présent sur l'air du bois ! lairdubois.fr/..._comment_218839
Nous sommes sur ce pas à pas avant tout, pour apprendre à travailler les bois en arêtier, donc ci dessous j'ai tracé en miroir depuis l'épure, une face versant assemblée petit cadre traditionnel (tenons,mortaises, moulure, rainure, et panneau plate bande) !
Sur l'emprunt d'élévation, nous pouvons tracer le Plan de coupe des éléments constituants la face versant en détail , pour avoir toutes les cotes d’usinages !
Ici nous découvrons pourquoi savoir tracer des épures de fabrication en pratique !
Nous traçons donc nos quatre faces versants depuis un seul tracé d'épure qui nous déjà à donné après avoir dessiné une face versant toutes les mesures du débit et de corroyage de nos bois (montants, traverses, panneaux) .
Une épure sert traditionnellement à tracer les bois par positionnement et "piquage" (relevé des trait depuis l'épure sur le champs des pièces), assurant ici un travail de précision, sans calculs mathématiques long et compliqués pour beaucoup, à effectuer et retranscrire !
Dans cet exercice, on découvre l'utilité d'une pénétration perpendiculaire (expliqué dans le chapitre précédent(choix)), qui nous permet de travailler les champs d'équerres de façons classiques aux machines avec le parement sur la table .
Tracé et exécution d'une pyramide irrégulière en panneau de 22 mm :
Ajouter de l'épaisseur aux faces d'une pyramide irrégulière, complique un peu plus l'exercice, car en effet nous savons qu'il faut une vue supplémentaire de coté dans la mise en page de l'épure!
A/ La mise en page de l'épure,et le tracé complet utile se posent classiquement . On découvre ici qu'il faut tracer les épaisseur désirée sur les deux vues avant de projeter tous les points de l'une et de l'autre vers la vue en plan et les développements des deux faces versants différentes .
B/ La subtilité à prendre en compte, est que les raccordements en chanfreins de coupes des panneaux sont différents puisqu'ils sont induits par deux pentes différentes, donc en plan nous nous sommes décalé de l’arête pour la partie inférieure de l’épaisseur de panneaux ! De plus au niveau de l'apex pour les faces versants les plus grandes, nous auront une coupe en plus à exécuter, induite par le niveau commun aux deux vues (élévation et vue de coté)
C/ Apres avoir tracés les bois depuis l'épure et le façonnage et ajustage ,nous montons la pyramide irrégulière désirée en un volume fini !
Tracé et exécution d'un tronc de pyramide irrégulière en panneau de 22 mm avec pénétration perpendiculaire :
Ici nous partons de l'épure précédente, et nous lui ajoutons un tronc et une pénétration perpendiculaire! Nous allons entrer maintenant véritablement dans de l’arêtier réfléchi pour des ouvrages !
En effet nous allons encore nous retrouver avec un nouveau choix à déterminer dans le projet fini de l'ouvrage avant d'en dresser l'épure .
A et B/ Pour la première étape de cette épure, J'ai dessiné l'exercice, avec le choix d'avoir toutes les traverses de l'ouvrage sur un même niveau, ce qui induit que je dois choisir l'emprunt de référence pour mon tracé de départ ! Ici j'ai choisi la face vue en élévation comme référence finie (ex parement d'un meuble), donc je trace mes bois sur l'emprunt de la vue de coté (ici traverses de 80 mm de largeur).
Les points des niveaux de traverses de références, sont ensuite projetés et rabattus sur l'élévation ! Aux intersections, sur les emprunts de l'élévation, nous traçons les traverses (en violet sur le dessin) .
En analysant le résultat, nous découvrons des sections de traverses complètement différentes de celles dessinées sur la vue de coté, mais placées sur un même niveau de l'ouvrage !
Dans le cas ou nous aurions tracées ces traverses de références sur l'emprunt d’élévation correspondant à la vue de coté, après projection, ce seraient les emprunts de la vue de coté qui auraient des mesures de largeurs différentes!
Enfin, si nous avions dessinés des traverses de largeurs identiques sur les emprunts des deux vues, elles ne seraient au final très logiquement pas au même niveau sur le pourtour de l'ouvrage .
Pour résumer le choix, pour un ouvrage de qualité nous pouvons choisir que l'élévation soit le parement de référence, ou bien les cotés de façon à être de niveau sur le périmètre . Ou pour un ouvrage sans importance , décider que toutes les traverses seront identiques mais donc pas au même niveau sur le pourtour (voir illustration en fin de chapitre)!
C/ Nous procédons classiquement au tracé des faces versants développés en vraies grandeurs depuis les vues réciproques en plan et élévation, et nous y traçons les montants désirés (ici 80 mm de largeur) .
ici des exercices dérivés de ce principe :
D/ En projetant tous les points depuis les faces versants développées en vraies grandeurs vers leurs vues respectives d'élévation et de coté, nous pouvons dessiner celles ci complètement !
E/ Depuis les intersections de génératrices réciproques sur la vue en plan, nous dessinons cette dernière complètement !
Sur la dernière vue de l'épure, j'ai enlevé la construction pour une vision globale du résultat, puis j'ai dessiné en miroir les développements des faces versants assemblées à petit cadre traditionnels.
Ici aussi en traçant perpendiculairement aux arêtes développées l'épaisseur des panneaux, nous pouvons dessiner aux intersections les sections des traverses et montants avec leurs mesures et angles en vraies grandeurs!
F/ Apres avoir tracés les bois depuis l'épure et le façonnage et ajustage ,nous montons la pyramide irrégulière désirée en un volume fini !
Les deux dernières illustrations définissent les différences de tracés énoncés plus haut !
ici un exercice possible a faire sur ces derniers exemples ,présent sur l'air du bois !
Tracé et exécution d'un tronc de pyramide irrégulière désaxée en panneau de 22 mm :
Pour finir avec cette présentation de développements avec notions d'épaisseurs, nous découvrons le principe avec une pyramide irrégulière et son axe décalé, ce qui induit quatre faces versants complètements différents les uns des autres !
Le principe ici reste le même, il faut juste apprendre à visualiser virtuellement dans l'espace pour raisonner avec logique .
A/ La mise en place de l'épure et tracés des épaisseurs sur le dessin primaire .
B/ Tracé de la vue en plan et du plateau avec leurs chanfreins coupes de raccordement.
C/ Tracés des faces versants développés complets .
D/ Apres avoir tracés les bois depuis l'épure et le façonnage et ajustage ,nous montons la pyramide irrégulière avec axe décalé désirée, en un volume fini !
En termes d'exercices, il n'y a pas de limites, donc à vous d'inventer des exercices d'expérimentations en fonctions des éléments de ce chapitre et de vos aspirations !
Caissette en arêtier assemblée à queues d’arondes de menuisier .
Cet exercice pratique intéressant est un classique d'apprentissage de l’arêtier ! Il donne un beau résultat utile, et permet d’appréhender en s'amusant la notion d'épaisseur .
A/ La mise en page de l'épure, est classique avec des arêtes en plan identiques régulières à 45° (comme si l'on avait divisé la base carrée globale d'une pyramide régulière en quatre carrés égaux, puis écartés et reliés) .
B/ Sur l'esquisse du contours de notre projet, nous traçons en élévation les épaisseurs des emprunts (20 mm d'épaisseur) ,ce qui permet par projections de ces nouveaux points de finaliser la vue en plan .
Puis nous traçons toujours sur l'élévation des queues d’arondes de menuisier en verticale dans un premier temps ! Ce premier tracé permet de faire nos divisions très simplement.
(J'ai intentionnellement fait des pentes forte aux queues d’arondes afin d'espacer les traits pour une meilleur lisibilité ) (pente de queues d’arondes traditionnelle entre 1/8 et 1/5)
C/ Par des fuyantes , nous projetons les points des queues d'arondes tracées en verticales vers l'emprunt !
Aux intersections des génératrices et des lignes d'emprunt et d’épaisseur, nous traçons les queues d’arondes biaises .
Puis nous développons nos faces versants en vraies grandeurs.
Enfin, depuis les queues d’arondes biaises vues de l'emprunt, nous traçons perpendiculairement à ce dernier, des lignes de niveaux, qui seront les mesures à reporter sur les faces intérieurs et extérieurs des bois à tracer !
Ici l'épure pratique d'atelier est terminée, elle doit être tracée échelle 1, et elle comporte toutes les informations nécessaires aux tracés de débit et d'usinages du projet .
D/ Le tracé complet de l'exercice, est ce que l'on demande normalement à un élève qui étudie le trait d’arêtier ! En effet tracer un dessin complet permet de travailler la vision dans l'espace !
La complexité des traits et des coupes à relier et coloriser en perspective géométrale intérieur et extérieur sur une même vue développée, et un classique incontournable ! (voir détails 1-2-3) (Rien n'empêche de faire les dessins en 2D sur logiciel comme je le fait ici pour progresser !) A vous de jouer !
Ci dessous , le tracé des bois depuis l'épure (tirés de large et d'épaisseur précisément), la progression d'usinage et le projet fini !
Ici un exemple présent sur l'air du bois !
En résumé de se chapitre, nous venons d'apprendre à assembler des bois sur les arêtes .
C'est à mon sens un très bon exercice intermédiaire avant de passer à l'apprentissage de l’arêtier traditionnel avec recherche d'angle de corroyage et assemblages de menuiserie et/ou de bois de charpente, que nous découvrirons dans les prochains chapitres .
Ici des exemples de travaux à faire depuis ce chapitre, présent sur l'air du bois !
Votre titre ici
Angles de corroyage , arêtes en vraies grandeurs
Nous entrons maintenant dans le vif du sujet d’arêtier, le fameux angle de corroyage si mystérieux et insaisissable pour qui n'a pas étudié le sujet !
Depuis le début de ce pas à pas, nous nous sommes familiarisés avec des pyramidaux développés à plat par leurs surfaces (herse), puis à leurs surfaces nous leurs avons apportés de l'épaisseur, pour apprendre à les jointer et pouvoir reformer le tout en volumes solides .
Ces derniers chapitres nous ont déjà donnés une vision globale des constructions en arêtiers! c'est à dire des faces versants reliés sur une arête saillante commune !
Nous allons à présent, chaque fois partir de ces mêmes arêtes saillantes, mais intégrées dans des volumes prismatiques (ex: pied de tabouret , chevrons d’arêtier, ...) pour arriver à déterminer un angle de corroyage, ce qui nous intéresse particulièrement dans le cas de constructions en bois d’arêtiers !
L'angle de corroyage
Situons déjà un angle de corroyage sur une pyramide régulière que nous connaissons maintenant parfaitement !
En géométrie académique, il se nomme l'angle dièdre formé par deux faces versants, mesuré dans le plan perpendiculaire à leur droite d'intersection l’arête .
Ci dessous, les illustrations nous montrent les deux angles que nous pouvons utiliser en pratique pour vérifier une construction pyramidale :
a/ L'équerrage depuis des lignes de niveaux situées sur le pourtour de la pyramide, en effet si la base est un carré ou un rectangle, une équerre à 90° pourra être utilisée elle aussi en position de niveau sur toute la longueur de l’arête .
b/ L'angle dièdre (de corroyage) sera pris depuis l’arête à l'aide une fausse équerre , placée perpendiculairement à celle ci sur ses deux faces versants simultanément .
Maintenant, nous dégageons de cette pyramide un prisme ,placé depuis l’arête !
Nous constatons que le principe s'applique parfaitement à ce prisme, car ici aussi nous pouvons vérifier sa bonne position grâce à l'équerre 90° placée sur deux lignes d'un niveau placé sur ses deux faces, et à la fausse équerre placée perpendiculairement à l’arête simultanément aux deux faces son angle dièdre (de corroyage).
Pourquoi rechercher l'angle de corroyage ?
Sur l'illustration ci dessous, nous avons placé en position depuis l’arête un prisme façonné d’équerre avec une face versant placé parallèle au plan, que se passe t'il ?
a/ Il est impossible de vérifier par des lignes de niveaux sa bonne position !
b/ Une de ses faces n'est plus parallèle au plan !
C'est ce que l'on appelle en charpente un "bois en dévers" ou "de/à dévers", utilisé fréquemment par les charpentiers qui ne reçoivent que du bois sur liste débités équarris qu'il faut cependant parfois placer sur un ouvrage en arêtier.
Le déversement d'une pièce équarrie sera donc pris en compte sur le dessin d'épure afin de pouvoir tracer et exécuter correctement les bois à assembler, c'est ce que l'on nomme "la recherche du devers de pas en charpente" (ex tréteau cadet à dévers youtube.com/wa...h?v=XalIZL6Znjk ) ,mais nous y reviendrons plus tard ! (voir plus bas chapitre tréteaux cadet)
En menuiserie ou en ébénisterie, nous rechercherons donc chaque fois l'angle de corroyage des bois d’arêtiers pour la raison esthétique d'avoir des faces de parements d'ouvrages affleurés de tout leurs éléments (montants, traverses, etc. ) parallèlement au plan (vue en plan)
Les tracés d'angles de corroyage sur épures :
Le principe pour trouver un angle de corroyage depuis l'épure est assez simple à comprendre, et sera appliqué pratiquement chaque fois, en charpente la technique du tracé se nomme le rembarrement !
Angle dièdre (de corroyage) de pyramide régulière :
Commençons par tracer l'angle dièdre d'une pyramide régulière pour visualiser facilement la technique .Sur les exemples d'illustrations j'ai tracé les épures de mise en page de deux pyramides à base carrées 400 mm x 400 mm identiques en plan, mais de différentes hauteurs, 500 mm et 150 mm .
1/ Depuis l'élévation, nous projetons en alignement la ligne de sol, depuis la vue en plan, nous projetons le point d'axe de la pyramide vers la ligne de sol. L’intersection des deux lignes nous donne le point de rabattement .
2-3/ Depuis le point de rabattement, nous traçons la ligne de sol rabattue parallèlement à l’arête vue en plan , et depuis l'élévation , nous projetons et rabattons la hauteur de la pyramide perpendiculairement à la ligne de sol rabattue .
4/ Aux intersections, nous traçons l’arête en vraie grandeur .
5/ Nous traçons perpendiculairement à l’arête en vraie grandeur ,la hauteur du triangle de cette derniere construction .
6/ Au compas depuis le sommet , nous rabattons la longueur de cette hauteur sur la ligne de sol .
7/ Nous projetons le point donné par le rabattement sur l’arête vue en plan .
8/ Depuis ce nouveau point d'intersection, nous traçons deux droites vers les angles de la base vue en plan, ce qui nous donne l'angle dièdre exact entre deux faces versants, soit l'angle de corroyage des bois !
Angle dièdre (de corroyage) de pyramide irrégulière :
Pour tracer l'angle dièdre d'une pyramide irrégulière le principe reste identique, mais nous n'avons plus la facilité du plan carré et ses diagonales d’arêtes en plan à 45° .
Sur les exemples d'illustrations j'ai tracé les épures de mise en page de deux pyramides à base rectangulaire 600 mm x 400 mm identiques en plan, mais de différentes hauteurs, 500 mm et 150 mm , ainsi que élévation et vue de coté pour faciliter la lecture .
1/ Depuis l'élévation, nous projetons en alignement la ligne de sol, depuis la vue en plan, nous projetons perpendiculairement une arête vue de dessus entière de la pyramide vers la ligne de sol. L’intersection des deux lignes nous donne classiquement le point de rabattement .
2-3/ Depuis le point de rabattement, nous traçons la ligne de sol rabattue parallèlement à l’arête vue en plan , et depuis l'élévation , nous projetons et rabattons le hauteur de la pyramide perpendiculairement à la ligne de sol rabattue .
4/ Aux intersections, nous traçons l’arête en vraie grandeur .
5/ Nous traçons perpendiculairement à l’arête en plan Une ligne fuyante vers la ligne de sol (Ici je me sert de l'angle extrême du petit coté du rectangle de la base).
6/ Depuis le point donné par cette dernière sur la ligne de sol, nous le relions par une droite perpendiculairement à l’arête en vraie grandeur ,puis nous rabattons ce point sur la ligne de sol !
7/ Nous projetons ce point donné par le rabattement sur l’arête vue en plan .
8/ Depuis ce nouveau point d'intersection, nous traçons deux droites vers les angles générés par la fuyante supplémentaire de la construction vue en plan, ce qui nous donne l'angle dièdre exact entre deux faces versants, soit l'angle de corroyage des bois !
Dans tous les cas, le principe s'applique, mais plus un pyramidal sera irrégulier, plus il faudra développer chaque arête en vraie grandeur, afin d'avoir tous les différents angles de corroyages du volume fini !
Enfin quand un angle de base est obtus, il faut passer par l'élévation pour trouver les points manquant en plan (rare dans nos professions, et les charpentiers passent par les délardements de pentes sur l’arêtier) !
Il est très important de comprendre ce petit chapitre, car la suite de l'apprentissage découlera directement de cette présentation !
En effet , l'angle de corroyage recherché et tracé, nous permettra ensuite de tracer les sections exacts "vue par bout" des bois désirés à placer dans des ouvrages . Donc à vos dessins d'études !!
A suivre , les tracés stéréotomiques de base en arêtiers droits !
Tracés et façonnages d'apprentissage des différents types d'arêtiers droits sur un plan carré
L’arêtier droit sur un plan carré régulier, est le passage d'entrée dans l’univers de la taille pratique des bois dans ces techniques ! En effet nous allons mettre à profit tout ce que nous avons déjà appris, et enfin travailler sur des exercices concrets!
J'ai fait les dessins qui suivent à partir de sections de bois assez imposantes pour bien éclaircir la lecture des tracés, évidement vous pouvez faire les exercices avec vos mesures et les bois à disposition dans vos chutes !
Arêtier droit sur plan carré avec faces d'aplomb délardées
Ce premier exercice, est généralement effectué par les jeunes charpentiers dans leurs tout premier apprentissage de l’arêtier ! Il se présente sur une base pyramidale classique ,sur laquelle nous allons placer depuis les arêtes, quatre chevrons de section 8/12 cm délardés (= angle de corroyage) avec coupes de raccordements .
1/ La mise en place de l'épure est ici sur la base d'une pyramide de 500 mm x 500 mm sur une hauteur de 400 mm en élévation.
Sur la vue en plan, nous pouvons d'ors et déjà tracer les chevrons vus de dessus (ici 80 mm) placés en axe par les arêtes, et se raccorderont en coupes croisillons au sommet (axe de la vue en plan).
2/ Nous construisons le développement du tracé de l’arête en vraie grandeur depuis celle ci vue en plan et la hauteur rabattue. Depuis cette dernière, nous construisons et traçons l'angle de corroyage sur la vue en plan.
3/ Depuis l’arête en vraie grandeur, nous traçons la face frontale du chevron désiré (ici 120 mm), ce qui nous donne déjà la longueur et la largeur du bois capable à débiter, puis nous projetons le nouveau point donné par la largeur sur la coupe au sol du développement vers la vue en plan pour tracer "L’empreinte au sol" de nos arêtiers.
Nous pouvons aussi connaissant cette largeur tracer la section "vue par bout" exacte avec ses délardements sur la vue en plan depuis l'angle de corroyage .
4/ Depuis l'empreinte au sol de la vue en plan, nous projetons la hauteur des délardements vers le développement, et depuis les intersections données sur la ligne de sol, en parallèle de l’arête en vraie grandeur, nous traçons les délardements en un trait car ils sont confondus .
Nous projetons ensuite tout les points nécessaires depuis l'axe de la vue en plan vers le développement pour tracer la coupe d'aplomb .
Enfin, depuis la vue en plan en projetant tous les points nécessaires vers l'élévation, nous pouvons tracer complètement cette dernière, ainsi que ses parties cachées en pointillés (exercice à faire d'office pour se familiariser avec la géométrie dans l'espace, ce qui sera très utile plus tard dans des tracés complexes) .
Nota: Généralement, quand les bois sont identiques sur une épure, nous n'en tracerons qu'un .Quand nous serons "aguerris", plus tard nous pourrons tracer qu'un quart partiel suffisant pour travailler !
Nous pouvons aussi faire économie de bois en prenant nos bois coupes dans coupes !
5/ Pour tracer les bois depuis l'épure, ici il faut "piquer", c'est à dire placer la pièce de bois équarrie bien en position depuis le tracé, puis relever très précisément les génératrices sur deux champs d'une première pièce, puis tracer avec les autres tous maintenus ensembles .
Ensuite il faut faire les coupes extrêmes d'aplombs biaises au sommet et de niveau au sol, puis ajuster les pentes de coupes des raccords (nous les positionnons à l'épure pour des vérifications) , et enfin nous exécutons les chanfreins de délardements.
ici exemples présent sur l'air du bois
Arêtier droit sur plan carré avec faces parallèles
Ici un premier exercice de menuisier apprenant l’arêtier, en effet les faces seront corroyées parallèlement suivant l'angle de corroyage dressé (classiquement à la raboteuse) .
1/ La mise en place de l'épure est ici sur la base d'une pyramide de 500 mm x 500 mm sur une hauteur de 400 mm en élévation.
Sur l'élévation, nous traçons arbitrairement une largeur vue frontalement désirée aux emprunts (ici 50 mm).
2/ Depuis les coupes au sol de l'élévation, nous projetons leurs points vers la vue en plan, puis sur cette dernière, nous traçons et matérialisons les empreintes au sol des quatre montants.
3/ Depuis les points d'angles des empreintes au sol vue en plan, parallèlement aux arêtes, nous traçons les bois et leurs coupes croisillons vus de dessus .
4/ Nous construisons le développement du tracé de l’arête en vraie grandeur depuis celle ci vue en plan et la hauteur rabattue. Depuis cette dernière, nous construisons et traçons l'angle de corroyage sur la vue en plan.
Nous projetons ensuite les points d'angles depuis l'empreinte au sol vers le développement .
5/ Sur le développement, nous traçons les autres arêtes en parallèle de l’arête développée en vraie grandeur, puis nous rabattons au compas et projetons depuis la construction de l'angle de corroyage les points générés par le dernier tracé d’arêtes vers la vue en plan.
Les intersections de ces génératrices et des arêtes vues en plan ,nous donnes le tracé de la section exacte vue par bout des bois à corroyer .
ici un exemple présent sur l'air du bois :
Ce dernier tracé de base d'apprentissage nous apprend une chose, c'est que l'on découvre la section vue par bout à corroyer, seulement à la fin du tracé de l'épure !
Meme si cet exercice est intéressant et permet de tracer facilement une épure, il ne permet pas de décider au départ les mesures exactes que l'on désireraient dans un ouvrage finalisé de qualité .
C'est une erreur que font beaucoup de novices (moi le premier il y à déjà bien longtemps), nous avons tracés arbitrairement 50 mm de largeur vue sur l'élévation, mais au final les faces vues de nos bois feront 52,1 mm ?
Pour remédier à cela, pour faire des travaux de menuiserie et d’ébénisterie corrects (par exemple des montants et des traverses de même largeur), nous devons apprendre à tracer nos épures avec des largeurs de bois vues désirées au départ chaque fois !
1/ La mise en place de l'épure reste identique mais juste pour le contours global !
2/ Apres avoir développé l’arête en vraie grandeur, extrait l'angle de corroyage et l'avoir tracé sur la vue en plan, c'est ici que le principe diffère du précédent!
Sur l'angle de corroyage, nous traçons cette fois la section vue par bout désirée de nos bois (ici nous désirons que nos faces finies feront 60 mm de largeur), donc nous traçons les largeurs des faces voulues, puis nous traçons les faces internes parallèlement .
Il résulte de l’opération la section exacte en mesures et d'angles de nos bois à corroyer !
Sachant que plus on change l'angle de pente des faces versants, plus la vue par bout se déformera, mais ce principe appliqué permettra chaque fois des largeur constantes (illustration 2 bis)!
3/ Nous traçons parallèlement aux arêtes en plan les bois vus de dessus en fonction de la vue par bout tracée précédemment. Puis nous traçons les empreintes au sol .
4/ Le tracé final de l'épure reste classique en projetant tous les points vus en plan vers le développement et l’élévation pour le finaliser .
5/ Le tracé des bois et exécution des bois différent complètement par rapport aux bois faces aplombs de charpente ! En effet nous placerons sur l'épure un bois non équarri, mais raboté fini avec l'angle de corroyage .
Donc le bois placé sur le développement ne sera pas aisé à piquer, puisqu'il correspond aux arêtes et serait en position instable sur une seule et nous devrions utiliser des cales de devers !
Pour remédier à cela, nous employons une technique simple et précise d'alignement perpendiculaire de tous les points de coupes nécessaires aux tracés, de part et d’autre du développement en vraie grandeur.
Nous plaçons le bois à plat sur une de ces faces, puis nous remontons et traçons à l'équerre les points donnés par les lignes sur le pourtour de notre pièce, et enfin nous relions ces points donnés par les tracés d'équerre aux arêtes pour finaliser nos ligne de coupes.
Pour les autres pièces, l'emplois de plusieurs sauterelles (fausses équerres) est conseillé pour la précision et le gain de temps , et nous sommes en menuiserie, donc nous devons appliquer un établissement de montants gauche/droite sur deux faces de pièces pour ne pas se perdre .
Il nous reste à exécuter et ajuster les coupes en prenant soin de vérifier à l'épure la construction finalisée .
Nota : Le principe des bois rabotés en faces parallèles, permet de construire rapidement des ouvrages pratiques sans notions vraiment esthétiques (ex tabouret marchepied) ,en effet les arasements pour d'éventuelles traverses, sont biais dans deux sens ! Pour faire des ouvrages aboutis avec des assemblages plus aisés, le principe suivant avec champs d'équerres sera la norme de qualité de travail en menuiserie et ébénisterie .
ici un exemple présent sur l'air du bois :
Arêtier droit sur plan carré avec champs d'équerres
Maintenant, nous allons donc tracer ce qui est la méthode d’arêtiers la plus aboutie en menuiserie et ébénisterie !
En effet la vue par bout désirée et tracée sur l'angle de corroyage , nous donnera des champs d'équerres, permettant ainsi d'usiner les bois aux machines classiquement sans avoir à contre caler les angles (mortaiseuse, toupie, etc.), pour obtenir du travail d'assemblage petit cadre de qualité et simplifié .
Les tracés d'apprentissages si dessous peuvent être issus d'une même épure, car depuis la vue par bout de section entière (4 cotés), deux autres possibilités de sections peuvent être exercées (5 ou 6 cotés). Nous analyserons les avantages et inconvénients de ces trois choix possibles à la fin du chapitre.
1 et 2/ La mise en page de l'épure et le tracé de l'angle de corroyage restent communes aux exercices précédents !
Sur l'angle de corroyage construit, nous traçons la vue par bout désirée, ici des faces de 60 mm, avec des champs d'équerres entiers. Ce premier arêtier à champs d'équerre, en l'état utilise beaucoup de bois dès que la pente des versants deviens faible, en plus d'une esthétique incertaine !
2a/2b/2c/ C'est ici que le choix de section s'impose suivant l'ouvrage que l'on doit faire ! En effet depuis la vue par bout entière (2a)(violet clair sur le dessin) , nous pouvons tracer deux autres possibilités!
2b/ Une vue par bout et champs d'équerres à 5 cotés ( 2 faces, 2 champs, et une face commune aux deux arêtes des champs) (violette foncée sur le dessin).
2c/ Une vue par bout et champs d'équerres de section creuse à 6 cotés (2 faces, 2 champs, 2 faces inférieures creuses) (bleu ciel sur le dessin).
Ces deux derniers principes (2b-2c)permettent un économie de bois en traçant nos champs d'équerres en fonction de l'épaisseur de futures traverses, ce qui donnera un affleurement esthétique de l’intérieur d'un ouvrage (ex pour une jardinière) .
3a/ L'épure complète du principe avec la section entière, nous montre que le tracé est assez simple.
L'analyse du résultat :
a/ Les empreintes au sol sur la vue en plan sont "déformées" en pointes donnant une grande masse de bois . En effet plus la pente de versant sera faible, plus la masse de bois sera conséquente et inesthétique !
b/ Les tracés et exécution des coupes aux sol et d'aplombs sont ici assez simples car générées par seulement quatre arêtes.
c/ Seulement deux arêtes sont confondues sur le développement.
3b/ L'épure complète du principe avec la section à cinq cotés, donne un tracé plus complexe car généré par cinq arêtes.
L'analyse du résultat :
a/ Les empreintes au sol sur la vue en plan, sont de fait plus abouties en terme d'esthétique, elles projettent vers le développement et l'élévation deux arêtes supplémentaires à raccorder pour les coupes.
b/ Les tracés de coupes d'aplomb et au sol demandent plus de réflexion pour raccorder les points de coupes.
c/ Sur le développement les quatre arêtes des champs sont confondues deux par deux.
3c/ L'épure complète du principe avec la section à six cotés dont deux en creux, donne un tracé encore plus complexe car généré par six arêtes dont une en creux .
L'analyse du résultat :
a/ Les empreintes au sol sur la vue en plan comportes deux cotés en creux parallèles aux faces versant vus, reliés par une arête en creux à projeter aussi vers les autres vues .
b/ Les tracés de coupes d'aplomb donnent des lignes parallèles sur le développement .
c/ Sur le développement, l’arête en creux doit être tracée en partie cachée pour déterminer les points de coupes d'aplombs .
Positions des bois à l'épure des trois principes arêtiers à champs d'équerres, pour les tracés et contrôles des exactitudes d’exécutions .
Pour la fin de ce premier chapitre concernant l'apprentissage pratique, je conseille de faire les épures le plus proprement possible sur un support stable, car elles seront reprises dans la suite des exercices quand nous placerons des éléments (ex traverses) .
La même chose pour les bois, ils serviront aussi pour la suite, en effet comme ils sont à champs d'équerres, nous pourrons les retravailler !
Tracés et façonnages d'apprentissage des différents types d'arêtiers droits sur un plan rectangle
Nous abordons dorénavant, les arêtiers sur plans rectangulaires, c'est le passage le plus aisé pour acquérir la technique de base pour des tracés irréguliers! En effet dès que l'on sort d'un pyramidal régulier (arête a 45° en plan) , il faut multiplier les points que génèrent plusieurs faces versants différents.
Arêtier droit sur plan rectangle avec faces d'aplomb délardées
Ce premier tracé issus de la charpente, facilitera la compréhension par sa simplicité, en plus d'une réflexion faisant appel à la logique qui deviendra systématique à l'avenir .
1-2/ La mise en place de l'épure est classique, une pyramide irrégulière sur un plan rectangle de 500 mm x 350 mm, avec une hauteur de 200 mm .
Cette construction de base, comportera donc une vue de coté supplémentaire, qui sera bien utile plus tard pour visualiser les vues frontales des coupes, et quand il faudra tracer des informations sur les différents emprunts !
Le dessin n°2 nous détaille le tracé en vraie grandeur de l’arête, puis par projection vers la vue en plan l'angle de corroyage .
Depuis cet angle de corroyage, il faut tracer le bois d’arêtier en plan, mais ici nous devons décaler son épaisseur de l’arête vue en plan, grâce à un tracé spécifique appelé le dévoiement en charpente afin d'avoir au final, des retombées de délardements identiques pour ne pas affaiblir la pièce par un trop gros enlèvement de bois, et faciliter les tracés ultérieurs.
Sur le détail 2b, nous apercevons les différences des vues par bouts dues aux tracés à l'axe et décalé de l’arête! Les débutants (et moi le premier il y à longtemps), font l'erreur de tracer les bois en axe dans de l’arêtier irrégulier de charpente, ce qui compliquera les tracés ultérieurs de raccordements ainsi que l'usinage des bois.
Le tracé se fait par un coup de compas pointé à l'épaisseur de bois désiré (ici 60 mm), sur une droite tracée perpendiculairement à l’arête a l'angle du lattis (extrémité de l'angle du plan).
Depuis ces deux points ainsi définis sur la droite, nous les projetons ensuite perpendiculairement sur le lattis, ce qui nous donne le décalage précis pour tracer les arêtes des faces versants vue de dessus. Ce principe est applicable et pratiqué en charpente seulement! Car menuiserie ou ébénisterie nous procéderons autrement pour des raisons esthétiques.
3/ Une fois tracé l'épaisseur de bois en plan, nous pouvons tracer tous les bois de l'ouvrage ainsi que leurs empreintes au sol. Depuis les points de la vues en plan, nous projetons le tracé de la pièce vue en développement de vraie grandeur.
4/ Le tracé complet de l'épure d'apprentissage, nous démontre la complexité accrue due au plan rectangle!
En effet le fait d'avoir cette fois deux pentes de versants différents, impliques des bois établis à gauche et à droite, donc une gymnastique de l'esprit pour retourner les traits des tracés sur les bois à façonner.
5/ Pour tracer les bois depuis l'épure, ici il faut "piquer" comme pour l'exercice en régulier face aplomb du dernier chapitre.
Ensuite il faut faire les coupes extrêmes d'aplombs biaises au sommet (deux coup de scie) et de niveau au sol (un coup de scie) , puis ajuster les pentes de coupes des raccords (nous les positionnons à l'épure pour des vérifications) , et enfin nous exécutons les chanfreins de délardements, en prenant bien soin d'avoir des pièces à droite et à gauches en miroir.
Ici un exercice présent sur l'air du bois :
Arêtier droit sur plan rectangle avec faces parallèles
Nous entrons cette fois en menuiserie, avec des bois corroyés en faces parallèles !
Le tracé d'apprentissage qui suit sera effectué avec des faces versants de parement d'inégaux en largeurs, ce qui donnera des empreintes au sol carrées et quatre arêtes en plan. En effet l’arête supérieur et inférieure ne sont plus confondues.
1-2/ La mise en place de l'épure reste classique, une pyramide irrégulière sur un plan rectangle de 500 mm x 350 mm, avec une hauteur de 200 mm .
Cette construction de base, comportera donc aussi une vue de coté supplémentaire!
Le dessin n°2 nous détaille le tracé en vraie grandeur de l’arête, puis par projection vers la vue en plan l'angle de corroyage .
Sur cet angle de corroyage, nous traçons la vue par bout désirée de section de bois corroyée. Depuis ses angles, nous traçons en parallèle de l’arête principale, les deux arêtes latérales et l’arête inférieure.
Nota : Sur l'agrandissement de détail, nous avons les deux solutions de tracés de la vue par bout.
A savoir avec une seule face définie qui donnera une empreinte carrée au sol (fig 2), et avec deux faces arbitrairement égales ,qui donneront une empreinte rectangulaire au sol (Fig 2b).
Au final que ce soit pour l'une ou l'autre situations, le principe du tracé de l'épure est strictement identique ! Donc je n'ai tracé dans ce paragraphe qu'un exercice partant de l'empreinte au sol carrée.
3/ Depuis la construction de base, nous traçons en plan tous les bois vus de dessus, puis nous projetons les points vers le développement d’arête , et nous traçons la pièce en vraie grandeur.
4/ L'épure complète d'apprentissage, représente la pièce sur toutes les vues avec les coupes de raccordements au croisillon d'apex.
J'insiste ici sur la propreté et la précision que l'on doit apporter sur une épure, car en effet les imprécisions peuvent se cumuler à mesure que l'on complexifie un projet. La solution la meilleur de vérification restera toujours de projeter un même point sur toutes les vues, ce qui permet de détecter les erreurs.
5/ Positions des bois à l'épure pour les tracés et contrôles des exactitudes d’exécutions .
Arêtier droit sur plan rectangle avec champs d'équerres
Comme sur un plan carré, l’arêtier avec champs d'équerres sur un plan rectangle nous donne trois possibilités esthétiques de vue par bouts : Quatre arêtes, cinq arêtes ou avec creux inférieur et six arêtes.
1-2/ La mise en place de l'épure reste classique, une pyramide irrégulière sur un plan rectangle de 500 mm x 350 mm, avec une hauteur de 200 mm .
Cette construction de base, comportera donc aussi une vue de coté supplémentaire!
2/ (En jaune): Apres avoir tracé l'angle de corroyage, nous traçons la vue par bout (deux faces de 50 mm) et deux champs d'équerres qui se rencontre en un point d'intersection qui déterminera l’arête inférieure .
Comme précédemment sur plan carré, cette vue par bout donnera des bois entiers avec quatre faces corroyées finis peux esthétiques ,mais nous traçons quand même l'épure pour ce principe, qui nous permettra encore une fois de visualiser dans l’espace afin de faciliter les prochains tracés!
2a/ (En violet): Depuis la vue par bout entière à 4 arêtes, nous traçons aux deux champs d'équerres l'épaisseur de traverses supposées (ici 30 mm) qui nous donnent deux point à relier pour la face inférieure des bois .
Ce tracé induit donc cinq arêtes distinctes en vue de dessus . Ce principe est le plus couramment utilisé, pour l'économie de bois et esthétiques des projets (ex: intérieur coffre)
2b/ (En bleu): Tracé similaire au dernier ci dessus, sauf que depuis les points des champs, nous traçons des faces creuses parallèles aux faces versants, ce qui donne en creux une arête supplémentaire .
Ce dernier tracé est utile en cas d'affleurement de tous les bois vus de l’intérieur d'un projet (ex: jardinière) mais nécessite plus de tracé et de façonnage !
3-3a-3b/ Les vues par bouts des trois principes, nous donnes toutes les informations pour tracer les bois en plan avec leurs empreintes au sol ainsi que leur coupes croisillons de l'apex .
Enfin à ce stade, nous traçons par rembarrement (rabattement à l’équerre depuis l’arête en plan) les développements des bois en vraies grandeurs
4-4a-4b/ A cette étape, nous obtenons l'épure finie pratique pour l'usinage, en effet tous les points utiles visibles ou en lignes cachés sont présents, ainsi que les bois en vrais grandeurs pour nous permettre le débit et taillage complet de l'exercice.
Ce dernier tracé, n’émancipe pas le fait de tracer l'épure complète d'étude d'apprentissage .
5/-5a-5b/ Les épures d'exercices complets avec toutes les vues tracées, et les bois sur l'épure .
En résumé des deux derniers chapitre :
Pour tous ces exercices d’arêtiers droits sur plan carré et rectangulaire, il faut chaque fois imaginer seulement trois coups de scie pour exécuter les coupes sur chaque pièce de bois ! A savoir deux sections pour la coupe d'aplomb au croisillon, et une pour la coupe au sol .
Si cette logique n'est pas respectée en visualisant le dessin de détails des coupes sur les différentes vues, c'est qu'il y a des erreurs !
ex de réalisation :
Tracés et façonnages d'apprentissage des types d'arêtiers cintrés et courbes depuis un plan carré
Dès que nous maîtriserons la logique des tracés et d’exécutions d'arêtiers droits (obligatoire), nous pouvons commencer à apprendre les tracés courbes !
Le principe est identique au droit sur plan carré, mais les versants ici cintrés à l'emprunt d'élévation, doivent être divisés en un nombre de points suffisants pour développer précisément une arête que sera de fait en courbe elliptique .
Principe du développement d’arêtes courbes sur un plan régulier
Nous allons ici nous démarquer de ce que l'on à vus en développement herse à plat sur papier et panneaux ! En effet pour concevoir des arêtiers en courbes, nous allons aborder la "stéréotomie de pièces", c'est à dire dessiner géométralement ces bois afin de déterminer des blocs de bois équarris capables de les contenir, et de fait pouvoir les débiter/corroyer, les tracer et les exécuter dans l'espace.
Nous en avons eu un avant gout avec les arêtiers droits en traçant les pièces géométralement depuis une arête en vraie grandeur, mais la technique était facilitée grâce à toutes les arêtes parallèles les unes aux autres pour les reconstituer !
Nous commencerons ce chapitre par le développement d’arêtes courbes, avant d'y ajouter des épaisseurs de bois, en effet ce principe de base sera commun à tous les tracés complexes futurs, et doit donc être maîtrisé avant d'approfondir !
1/ La mise en place de l'épure pour de l’arêtier cintré ou courbe reste classique, une vue en plan (ici 500 mm x 500 mm) et une élévation avec sa base de 500 mm et deux emprunts formant un plein cintre (dôme de pyramide) .
2/ Sur un des emprunts, nous divisons le cintre en parties égales depuis son centre avec la technique des cordes. Puis nous construisons le point de rabattement et la ligne de sol parallèlement depuis l’arête vue en plan .
3/ Depuis l'élévation nous projetons tous les points vers le développement, et vers la vue en plan .
4/ depuis la vue en plan, nous projetons les points générés vers les génératrices réciproques du développement, et aux intersections, nous traçons à l'aide d'une cerce la courbe développée en vraie grandeur .
5-6-7/ Pour des cintres autres que plein cintre, le principe est identique ! Tant que les emprunts seront tracés à base d'arc de cercles centrés, les divisions se font aisément par les cordes, puis classiquement nous projetons les points et aux intersections des génératrices réciproques, nous traçons les courbes d’arêtes développées en vraies grandeurs .
8/ Des que les courbures d'emprunts ne sont plus divisibles par des cordes ou un cheminement de compas, nous utiliserons des lignes de niveaux, par exemples comme pour un pied de commode tombeau galbée de face et de coté . Ce principe souvent utilisé au départ pour faire fabriquer des appliques en bronze par exemple , ou en faisant le tracé inverse pour galber un pied en bois à façonner en fonction d'un bronze courbe préexistant . (J'y reviendrais dans un chapitre futur)
Arêtier courbe sur plan carré avec faces d'aplomb délardées
Comme précédemment, nous commencerons par un arêtier de charpente ! En effet la compréhension est assez simple et permet de fabriquer un premier exercice en courbe intéressant et spectaculaire pour un novice dans ces techniques, de plus les arêtes positionnées à 45° en plan facilitent grandement les projections et confondent les arêtes développées, ce qui ne sera plus le cas dans de l'irrégulier en plan .
1/ Sur l'épure après avoir développé l’arête en vraie grandeur, nous plaçons les bois désirés vus en plan (sur l'exemple, arêtiers de 60 mm d'épaisseur et un chevrons à l'emprunt de 60 mm ).
Le tracé de l’arêtier en plan, nous donne déjà les arêtes des délardements, et leurs mesures de retombées à la base (30 mm en violet))
Pourquoi un chevron ? car Il sera nécessaire plus tard de l’élever sur l'élévation de façon à avoir la retombée de bois des faces d'aplomb sur les bois d’arêtiers, grâce à sa coupe verticale vue à l'emprunt (ici c'est un vrais chevron d'emprunt en charpente) .
2/ nous reportons au compas, la mesure de retombée vue de dessus en plan (30 mm) sur toutes les lignes de niveaux du développent depuis l’arête en vraie grandeur, puis aux intersections, nous traçons à la cerce la seconde courbe développée. En ombrageant le dessin, nous obtenons les deux délardements confondus de la pièce vue géométralement .
Avec le compas, nous traçons le chevron d'emprunt désiré (ici largeur 60 mm) sur l'élévation, puis en projetant ses points de coupes vus en plan vers l'élévation, nous traçons ce dernier, et en ombrageant la coupe et sa face nous le découvrons entier vu frontalement. Ce dernier tracé, nous donne la hauteur de coupe à reporter sur les génératrices verticales du développement depuis la courbe de délardements pour y tracer la retombée de bois utile inférieur de l’arêtier.
3/ En traçant perpendiculairement à la courbe des délardements la hauteur de coupe sur le développement et en projetant les coupes depuis la vue en plan , nous obtenons l’arêtier entier vus géométralement .
En traçant un rectangle tangent aux points extrêmes du développement de la pièce complète, nous obtenons la longueur et la largeur du bloc de bois capable de l’accueillir 433,1 cm x 135,4 cm .
4/ Dans le dessin d'étude complet d'apprentissage, nous découvrons le principe de dessiner les pièces vues géométralement en élévation, qui nous procure une vue frontale en position recto-verso .
Depuis les sections perpendiculaires à la courbe d’arête en vraie grandeur du développement, en prenant les hauteurs de retombées des délardements et des faces, nous pouvons tracer chaque section vue par bout, ce qui sera utile plus tard dans des ouvrages plus complexes .
L'usinage des pièces courbes d’arêtiers
A ce stade de l'apprentissage, il est important de faire une parenthèse pour visualiser les techniques de bases de la taille de ces bois singuliers !
En effet ce premier exercice (charpentier), est le bon moment pour commencer à appliquer ce qui sera le principe général de la suite des façonnages de bois courbes divers d’arêtiers.
Le piquage : C'est l'action de relever le tracé utile de façonnage depuis une épure pour l'apposer sur les bois à usiner ! En effet ce sont les points de coordonnées qui permettront de tracer des courbes linéairement propre de références précisément, ce qui est de fait un peu plus compliqué que le simple rembarrement dans les arêtiers droits.
Il existe plusieurs procédés de transferts généraux :
a/ Le piquage traditionnel:
Aux mesures tracées sur l'épure, nous équarrissons un bloc de bois capable, que nous plaçons ensuite en position sur le développement .Puis nous remontons toutes les génératrices horizontales et verticales utiles sur les champs et bouts de la pièce. En reliant ensuite sur la face les génératrices réciproques des champs et des bouts, aux intersections nous pouvons tracer à l'aide d'une cerce la courbe de l’arête principale.
Enfin à l'aide d'un compas pointes sèches, nous reportons depuis la courbe d’arête principale , toutes les retombées de délardements et d’arêtes inférieures prises sur l'épure. Ce principe nécessite beaucoup de bois et de temps de traçage , il doit être réservé qu'en cas de pièce unique .
b/ Le piquage au compagnon:
Un compagnon de traçage est un outil très pratique qui est constitué d'une règle contre-calée à l'épaisseur du bloc à tracer . Il permet de transférer directement et précisément sur la face ,les génératrices prises depuis l'épure !
Ce principe, très utilisé en construction d'escalier, permet de ne corroyer que les faces en épaisseur, sans s'occuper des champs ! En effet il est préférable de débiter les pièces dans du bois déjà cintré naturellement dans ce genre d'ouvrage, pour un soucis de solidité, d’esthétique et de gain de bois .
c/ La fabrication d'un gabarit: C'est une des méthode les plus utilisée, surtout en cas de plusieurs pièces en série! On façonne un gabarit (carton, contreplaqué fin, medium, etc.) qui contiendra touts les informations, que l'on applique sur les pièces de bois, comme un patron pour du tissus. Cela permet un débit optimum sur des bois à débiter déjà cintrés naturellement notamment et un principe nomade qui permet une grande liberté .
Il est possible aussi de travailler avec gabarit épais et bouffe-tout à la toupie (Travail dangereux en cas de grosse épaisseur).
d/ le collage du tracé d'épure papier sur les bois: Ce dernier procédé est assez contemporain et d'une précision redoutable! Grâce aux techniques d'infographies nous pouvons imprimer les dessins en plusieurs exemplaires, que l'on colle directement bien marouflé directement sur les bois rabotés d'épaisseur avant de les exécuter aux tracé de ces transferts .
Ces deux derniers procédés, permettent aussi de façonner un bois par collage de la chute de la courbe creuse sur la partie qui sera bombée , donc un gain de bois débité relatif .
Positions des bois à l'épure et façonnage :
Le façonnage est simple pour ce principe charpentier, il faut donc chantourner et calibrer la pièce d’arêtier depuis sa courbe d’arête principale et inférieure, puis nous traçons les retombées de délardements .Nous traçons ensuite un trusquinage centré du champs délardé et nous exécutons les coupes de niveaux au sol et d'aplombs au croisillon de l'apex.
Enfin, suivant la proportions des pièces, nous taillons les délardements à l'aide des outils traditionnels (coups de scie et ciseaux à bois, wastringue, plane, râpe, rabot, etc.)
Les ajustages se font petit à petit en plaçant les bois à l'épure pour contrôler les concordances et la précision .
Dans l'absolu, tant que l'on arrive pas à tracer ce dessin complet, et d'en comprendre toute la logique, puis d'en tirer le façonnage abouti des bois, il faut persévérer et maîtriser cet exercice avant d'aller plus loin !
Ici un exemple présent sur l'air du bois
Arêtier courbe sur plan carré avec champs d'équerres
Ce premier exercice d’arêtier courbe avec champs d'équerre est assez brut dans sa finalité ! Il permettra néanmoins d'assembler des travaux ou nous devons assembler des traverses, des panneaux et des raccords (moulures, rainures, feuillures, avec un toupillage champignons ou un tarabiscot) .
A partir d'ici il est obligatoire d'utiliser des numéros et des lettres pour identifier les traits !
1/ Apres avoir développé la courbe de l’arête en vraie grandeur, nous traçons une empreinte au sol sur la vue en plan à une largeur de bois désirée (ici 60 mm).
Depuis cette empreinte carrée, nous alignons les arêtes secondaires, puis nous traçons en élévation l'emprunt que nous divisons par les cordes (ici en 8).
2/ Apres avoir numérotés tous les points de coordonnées rayonnants de l'emprunt, nous les projetons vers la vue en plan .
Les segments parallèles à la base (b-2, c-3, etc ...) depuis les arêtes latérales de la pièce vue en plan, nous donnent les arêtes inférieures des champs d'équerres que nous traçons .
La mesure de demi diagonale de l'empreinte au sol projetée vers le développement, puis tracée de niveau sur tous les points de la courbe d’arête, nous donne la courbe de retombées. Apres avoir tracé cette seconde courbe et ombré, nous obtenons les faces vues de coté en vraies grandeurs (ici confondues) .
3/ Nous projetons enfin les points d’arêtes inférieures (a-b-c ...) depuis l'élévation et la vue en plan vers le développement, puis aux intersections nous traçons la courbe d’arête inférieure en vraie grandeur.
Nous projetons enfin les traits de coupes du croisillon d'apex depuis la vue en plan vers le développement puis nous ombrons le tout pour obtenir la pièce complète vue de coté en vraie grandeur .
Cette épure est finie à ce stade pratique pour tracer et usiner les bois, les mesures du bloc capable se trouvent en plan pour l'épaisseur (84,9 mm) et sur le développement pour la longueur et la largeur (433 cm x 134 mm) en traçant un rectangle tangent aux points extrêmes de la vue .
4/ L'épure complète d'étude, permet de visualiser la pièce dans toutes les situations et de se familiariser avec la logique d’arêtiers cintrés.
Puis en traçant tous les rayons sur le développement, nous obtenons toutes les mesures de retombées qui nous permettent avec la mesure du capable en plan de tracer toutes les sections rayonnantes avec leurs angles de corroyage progressif de débillardements des faces et des champs .
En résumé de ce tracé d'épure, nous obtenons des bois d’arêtiers courbes avec des champs capables d’accueillir des traverses ,moulures, rainures, etc, assez facilement, dans une logique d'équerre petit cadre assemblé traditionnel ! Par contre les faces ne sont pas de largeur constantes ce qui gâcherais l’esthétisme dans des travaux de qualités supérieurs.
5/ Le tracé des bois se fait classiquement depuis l'épure en positionnant le bloc capable sur le développement et en piquant tous les points sur ses champs, ou avec compagnon, transfert, etc .. (voir plus haut).
Le façonnage se fait en trois étapes :
a/ Apres avoir tracé le bloc, nous chantournons et calibrons les courbes "mères" de l’arêtier .
b/ Nous retraçons sur les parties cintrées, tous les traits utiles de coordonnées de points, ainsi que les lignes d’arêtes (supérieure et inférieure).
Pour la ligne d’arête supérieure, c'est simple car elle est médiane de la largeur , donc avec une règle souple et un crayon c'est vite fait.
Pour les arêtes inférieures par contre, il faut prendre les points de largeur sur la vue en plan au compas et les reporter sur chaque rayons définis sur la pièce, puis à l'aide d'une cerce, nous relions les points (voir détail illustré) .
Nous traçons et exécutons ensuite les coupes du croisillons d'apex et de sol .
A cette étape, nous pouvons déjà positionner les bois sur l'épure pour ajuster les coupes et les divers réglages de positions justes .
c/ Enfin a l'aide des outils a mains (coups de scie, plane, wastringue, rabot à débillardé, etc ...) nous calibrons les faces et champs débillardés .
Nota : On devine bien ici l’intérêt de ne pas brûler les étapes, donc commencez bien par la méthode charpente avec face aplombs pour appréhender les principes (traçage et usinage en surfaces gauchies) !
Arêtier courbe sur plan carré avec Développement des faces et champs d'équerres
La maîtrise de l’arêtier se définit ici par le principe le plus aboutit par l'art du trait !
En effet ce tracé en deux temps par le développement d'une face, permet d'avoir des faces et champs constants mesurables sur toute la continuité des bois, permettant ainsi une esthétique dans les travaux de qualités supérieures en menuiserie et ébénisterie.
Par contre la technique complique les tracés par le surnombre de points de coordonnées et de génératrices à considérer .
1/ Apres avoir développé la courbe de l’arête en vraie grandeur de façon classique, nous traçons l'emprunt divisé en élévation a l'épaisseur des champs désirée (ici 30 mm) .
Puis nous traçons le développement d'une face par ses deux arêtes en parallèle (voir premiers chapitres).
2/ Depuis l’élévation, nous projetons les points de coordonnées (chiffres) sur l’arête principale de la vue en plan, et depuis le développement de la face, nous y projetons aussi les points de coordonnées (niveau 1-1', 2-2', etc..) réciproques .
Aux intersections, nous traçons à la cerce ou au pistolet les arêtes latérales courbes de la pièce vue de dessus .
3/ Depuis l'emprunt d'élévation, nous projetons les points inférieurs (lettres vers la vue en plan .
Aux intersections avec les lignes de niveaux (b-2',c-3', d-4', etc.) ,nous traçons a la cerce les courbes de champs inférieurs .
4/ En ombrant le tout, nous découvrons la pièce d’arêtier vue de dessus avec son empreinte au sol et ses champs distincts.(voir détail)
Aux points extrêmes du dessin, nous traçons le rectangle tangent du bloc capable qui nous donne déjà sa largeur 119,7 mm).
5/ En projetant les points de coordonnées (2',3', etc...) depuis la vue en plan vers les ligne de niveaux réciproques du développement de l’arête en vraie grandeur, aux intersections avec la cerce nous traçons la retombée des faces vues de coté (ici confondues).
Nous ombrons le dessin pour visualiser correctement l'ensemble .
6/ Pour finaliser l'épure pratique , il nous reste à tracer les arêtes (confondues) inférieures!
Nous projetons les points de coordonnées en lettres depuis l'élévation et la vue en plan vers le développement, puis aux intersections , à la cerce nous traçons les derniers courbes d’arêtes .
Nous traçons enfin la coupe de croisillon d'apex, et en ombrant le tout, nous découvrons la pièce d’arêtier entière vue de coté en vraie grandeur .
En traçant tangent aux points extrêmes un rectangle, nous obtenons la longueur et l'épaisseur du bloc capable (432,9 mm x 118 mm) .
7/ Pour parachever le dessin d'étude, nous traçons la pièce vue de dessous en vraie grandeur depuis le développement, et vue frontalement sur l’élévation .
Enfin, depuis les rayons tracés en section sur le développement , nous pouvons prendre toutes les mesures de retombées, que nous traçons perpendiculairement aux mesures des champs vus en plan, pour obtenir toutes les sections rayonnantes avec leurs angles de corroyage progressifs de débillardements des faces et des champs .
Cela permet aussi de vérifier le tracé, en effet toutes les sections doivent avoir leurs faces egales à 60 mm et leurs champs égaux à 30 mm .
L'épure complète d'étude finalisée de cette pièce, reste en général, le premier dessin ouvrant la porte aux complexités les plus audacieuses par la suite ! Sa compréhension et son tracé maîtrisé apporte toutes les réflexions logiques utiles à la suite des apprentissages en art du trait .
5/ Le tracé des bois se fait classiquement depuis l'épure en positionnant le bloc capable sur le développement et en piquant tous les points sur ses champs, ou avec compagnon, transfert, etc .. (voir plus haut).
Le façonnage se fait en quatre étapes :
a/ Apres avoir tracé le bloc, nous chantournons et calibrons classiquement les courbes "mères" de l’arêtier .
b/ Nous retraçons sur les parties cintrées, tous les traits utiles de coordonnées de points, ainsi que les lignes d’arêtes (supérieure et inférieure).
Il faut prendre touts les points de largeur sur la vue en plan au compas et les reporter sur chaque rayons définis de la pièce, puis à l'aide d'une cerce, nous relions les points (voir détail illustré) .
c/ Nous traçons et exécutons ensuite les coupes du croisillons d'apex et de sol .
A cette étape, nous pouvons déjà positionner les bois sur l'épure pour ajuster les coupes et les divers réglages de positions justes .
d/ Enfin a l'aide des outils a mains (coups de scie, plane, wastringue, rabot à débillardé, etc ...) nous calibrons les faces et champs débillardés .
Nota : On devine bien ici l’intérêt de ne pas brûler les étapes, donc commencez bien par la méthode charpente avec face aplombs pour appréhender les principes (traçage et usinage en surfaces gauchies) !
ici une vidéo intéressante pour ce dernier exercice bumic.fr/2019/...gnon-du-devoir/
Travaux pratiques d’arêtier : Tréteaux cadet pieds à dévers et pieds avec angle de corroyage
Je reprend ici l'écriture de ce pas à pas sur l’arêtier avec un premier projet pratique très classique chez les apprentis charpentiers !
Une paire de tréteaux dit "cadet" pour être utilisée en charges lourdes !
Ils ont les piétements en arêtier à l'image d'une mini charpente , ce qui leur confèrent une stabilité extrême sans possibilité de jeux (longitudinalement et latéralement) !
Plus on les chargent, plus ils sont stables ce qui n'est pas le cas de tréteaux avec des jambages d'aplomb .
Ils sont appelés "cadets", car à l'époque ils étaient plus petit que les tréteaux de scieurs de long !
Le principe ici sera double, à savoir que depuis une même épure primaire, nous aurons un tréteau avec pieds montants en "devers de pas", et l 'autre avec "angle de corroyage" des ses pieds montants !
Évidement nous pourrions les faire à nos mesures et sections de bois en fonction de nos besoins propres, voire compliquer les croix de st André et autres sans limites ! (voir illustration)
Dans notre cas j'ai pris le plus basique possible mais avec assemblages de menuiserie, pour se concentrer sur les deux possibilités d'apprentissage de base des piétements .
Une jolie trouvaille présente sur l'air du bois :
Pieds en devers et pieds corroyés avec angle :
Si vous avez bien étudié depuis le début de ce pas à pas, je n'ai pas besoin de présenter le principe de l'angle de corroyage ! Le résultat pratique est d'avoir une empreinte au sol faisant "lattis" (alignée) sur les deux versants de la pièce en arêtier !
Le "Devers de pas" lui est une variante qui permet de concevoir des projets d’arêtiers avec des bois équarris sans avoir à corroyer l'angle recherché ! (utile en charpente quand des pièces sont imposantes par exemple , c'est un gain de temps de ne pas avoir à les corroyer).
Le résultat pratique est que généralement un versant de la pièce d’arêtier fait lattis, mais l'autre n'aligne pas le tracé en plan de l'épure ! (au choix, lattis avec le "long pan" ou la "croupe")
De ce fait, il faut savoir le dessiner afin de pouvoir ultérieurement développer et tracer tous les bois d'assemblages avec des angles spécifiques !
Tracé de l'épure
Pour information, j'ai intentionnellement tracé l'épure échelle 1 complète, sachant que une demi épure à l'axe généralement est suffisante !
Mise en place de l'épure :
Sur un panneau de cp ou autre, nous dessinons déjà les contours de vues (en plan, élévation, et vue de coté) .
Ici nous traçons déjà la vue en plan et l'élévation avec les arêtiers en fonction de la traverse haute et du désafleur désiré des pieds (ici 10 mm) ,puis nous traçons la vue de coté .
Sur ces tracés "directeurs" , nous dessinons les éléments connus frontalement (traverse haute, croix de st André, traverses basses, partout ou c'est possible !
Tracé de l'angle de corroyage :
Celui ci se trace classiquement depuis la vue en plan et la hauteur, ce qui nous donne la vraie pente et longueur de l’arête ! Il est impératif de la tracer dans les deux cas !
Depuis cette construction, nous projetons et nous traçons l'angle de corroyage sur la vue en plan!
voir chapitre: Angles de corroyage, arêtes en vraies grandeurs .
Tracés des sections de pieds :
1/ Sur l'angle de corroyage en plan, nous traçons aux cotes désirées (ici 70 mm x 50 mm) la section du pied et ses faces parallèles pour le tréteau en arêtier classique .
2/ Sur l'angle de corroyage en plan, nous traçons aux cotes désirées (ici 70 mm x 50 mm) la section du pied d'équerre pour le tréteau en dévers .
Nota : Nous pourrions tracer la face faisant lattis au choix depuis la croupe ou le long pan ! (ici j'ai choisi la croupe !)
Tracés des empreintes au sol des deux principes :
1/ Pour tracer l'empreinte de pied d’arêtier classique vue en plan, il suffit de projeter des fuyantes depuis les angles de la section dessinée sur l'angle de corroyage parallèlement à l’arête vue en plan , puis de tracer des parallèles au lattis .
2/ Pour tracer l'empreinte de pied d’arêtier en devers de pas en plan, il faut projeter les points (a-b-c-d) de la section d’équerre dessinée sur l'angle de corroyage vers la ligne de sol de la construction de développement, puis de les rabattre au compas sur la section d'équerre !
Nous traçons ensuite des parallèles à l’arête en plan depuis les points de la section ! (ce qui nous donne déjà le lattis d'- a')
Depuis la section rabattue du développement, nous projetons parallèlement à l’arête ces points vers la ligne de sol, puis nous les projetons vers la vue en plan .
Les intersections des fuyantes nous donnent les autres points, et donc une fois reliés l'empreinte de devers vue en plan !
Épure d'étude, épure pratique :
Dans un apprentissage "à l'ancienne", nous devrions tracer les épures d'études de préférence à l'échelle 1/4 de manière à conserver précision et lisibilité !
Ci dessous, l'étude du tréteau avec le piétement corroyé à l'angle de corroyage recherché. On découvre un dessin de toutes les vues utiles bien éclaté avec un maximum de détails.
Ici , le développement en vraie grandeur ou "herse" chez les charpentiers, est rabattu depuis l'élévation et projections rabattues depuis la vue en plan .
Ci dessous, l'étude du tréteau avec le piétement à devers de pas. On ici aussi découvre un dessin de toutes les vues utiles bien éclaté avec un maximum de détails.
J'ai volontairement installé une autre implantation possible, sachant que le principe reste toujours identique.
Ici , le développement en vraie grandeur ou "herse", est développé depuis la vue en plan et projections rabattues depuis l'élévation .
En résumé, les épures d’études permettent de visualiser dans le détail tout un projet! Il faut dire qu'à l'époque sketchup n'existait pas et que les représentations ne pouvaient se faire que par "art du trait" !
L'épure pratique du tréteau avec angle de corroyage des pieds, s’exécute le plus simplement possible, afin de ne pas perdre en précision et lisibilité, ici tout le tracé utile est fait de fuyantes, mais généralement chaque fois que c'est possible, depuis un seul point commun de rebattement pour les 4 demies vues !
L'épure pratique du tréteau avec pas de dévers, s’exécute le plus simplement possible, comme le précédent afin de ne pas perdre en précision et lisibilité, ici tout le tracé utile est aussi fait de fuyantes depuis un seul point de rebattement pour les 4 demies vues !
Piquage et tracés des bois depuis l'épure :
Le piquage se fait sur les arêtes posées sur l'épure, depuis les rembarrements d'équerre de chaque point, que l'on trace ensuite avec une équerre sur toute la périphérie de la pièce !
Il faut ensuite faire une petite gymnastique de l'esprit afin de relier logiquement les bons traits d'angles depuis les bons points des arêtes .
Il est vivement conseillé d'identifier les génératrices avec des lettres ou chiffres ! (Je ne le fait pas systématiquement sur mes dessins, ce n'est as aisé avec sketchup )
Ici pour le tréteau à dévers de pas , le principe est assez simple , les arêtes se confondent sur l'épure de la herse !
Ici pour le tréteau avec angle de corroyage des pieds, le principe est un peu plus complexe, en effet il y a plus de traits à piquer !
Il est conseillé pour éviter des erreurs, de commencer par la traverse qui est un tracé simple depuis la vue en plan, qui nous apportera des informations de longueur de coupes, d'arasements et d'angles à vérifier en corrélation avec les tracés sur les pieds !
En résumé de cet exercice simple et utile, nous pourrons essayer les deux grands principes !
J'ai fait des fabrications plutôt de menuisier, avec des assemblages qui donnent un peu à réfléchir, ce qui est un peu le but en apprentissage!
Ci dessous, deux liens de constructions de tréteaux en arêtier dits "types Mazerolle" à construire rapidement avec un outillage limité .L'épure de base au début de ce chapitre est évidement compatible avec tout types de tréteaux en arêtier !
Nota : Les tréteaux sont assemblés traditionnellement par boulonnage des pieds au chapeau, et tenons mortaises ou coupes clouées aux traverses basses !
youtube.com/wa...h?v=XalIZL6Znjk
Tout est possible à partir d'un seul tracé directeur ! donc à vos chutes et construisez vous de jolis tréteaux solides.
Le mythique tréteau Buenos Aires !
Introduction du principe "tréteau buenos aires"
Ce chapitre, sera consacré au tréteau "Buenos aires", qui pour la petite histoire a été conçu par un compagnon charpentier du devoir de liberté, du nom de Joseph Denis Boucher dit « La Brie l'Ami du Trait » (1836-1911), expatrié fin 19 eme siècle en argentine .
compagnonnage....trait-1836-1911
Je remet aussi ici en avant le travail de sanglier, qui avait dérivé le principe en autant de projets différents intéressants.
Son travail remarquable, souffrait quand même à mon gout, d'un manque d'épures complètes traditionnelles, et d'explications claires, ne permettant pas aux novices (moi le premier) une lecture assez simple et détaillée du traçage à des fins d'exercices ou de constructions.
Donc ici, nous allons détailler le B-A BA de la technique, qui donne la porte ouverte à tout travaux ensuite étudiés!
J'ai du passer du temps a retrouver les codes du tracé de ces ouvrages, n'ayant que survolé le principe il y a déjà  plus de 30 ans !
plus de 30 ans !
Principe du tréteau Buenos aires :
C'est un volume pyramidal de base polygonale régulière (ou irrégulière, mais là c'est chaud! ), sur lequel viennent s'appuyer sur ces faces, des bois corroyés alignés sur chacune des arêtes de celle ci !
Ces pieds viennent s'entrelacer au sommet de la pyramide en un "noeud" aux arêtes communes sans aucun jours visible .
Ci dessous, détails du principe, et quelques exemples sur pyramides à bases triangulaire, pentagonale, et hexagonale .
C'est un système d'assemblages, qui laisse un champs infini en conceptions de projets, des que l'on a maîtrisé la base du traçage de l'épure, pour la recherche des coupes et entaillages divers (qui doit être très rigoureuse de précision) .
On peut imaginer plus tard, cette technique "d’arêtier" avec du cintre, du tournage, du chantournage et bien d'autres usinages !
Donc à vos crayons, règles et compas ! 
Buenos aires sur plan carré, pieds de section carrée en devers
C'est celui que l'on apprend en premier pour étudier cette technique fantastique !
Une pyramide à base carrée, sur laquelle quatre pieds de section carrée, sont plaqués sur les faces posés en devers alignés avec les arêtes .
Pour les exercices , et faciliter la lisibilité, j'ai pris des bois de section 50 mm x 50 mm corroyés, posés sur de petites pyramides !
Deux pieds suffisent pour tracer une épure utile !
1/ La mise en page de l'épure est assez simple ! Elle se présente par une vue en plan et une élévation vue de face de pyramide ou viendront ensuite se tracer les bois de l'ouvrage souhaité .
Comme on le voit sur l'élévation, pour déterminer la hauteur du tréteau fini, on relie au sommet de la pyramide de base, une seconde pyramide inversée .
Nota : Ici les deux volumes sont identiques pour faciliter l'étude ! Plus tard nous pourrons agrandir ou rétrécir la pyramide inverse en fonction d'écartements désirés .
2/ Communément comme dans tout travaux d’arêtier, nous traçons déjà l'indispensable angle de corroyage (dièdre), sur lequel nous tracerons ensuite la section désirée de nos pieds .
Ici une section carrée (50 mm x 50 mm), depuis l’arête de l'angle de corroyage.
Cette dernière opération nous donne le profil sectionnel de la future entaille ainsi que la mesure sa retombée de champ en alignant par une fuyante l'angle dièdre . (en orange sur le dessin)
Nous traçons ensuite sur l'élévation l'emprunt (largeur 50 mm). Ce qui nous donne les coupes au sol et de niveau vus en élévation .
3/ Depuis les quatre points de la section carrée et le point de l'entaille vus en plan, nous alignons à l'aide de fuyantes parallèles à l’arête en plan, toutes les arêtes de la pièce.
4/ En projetant les points des coupes au sol et de niveau de l'élévation vers la vue en plan, nous obtenons les points de tracé des empreintes au sol et coupe de niveau .
Nous traçons les coupes, et nous les matérialisons.
Sur l'empreinte au sol vue en plan (en orange), nous projetons l'entaille depuis le vue par bout (section) et nous la traçons !
Je rappelle ici que l'emplois de chiffres et de lettres pour nommer les points et fuyantes est fortement recommandé .
5/ Apres avoir rabattu au compas les points de l'empreinte au sol et des fuyantes du premier vers le second pied placé sur la seconde arête de la pyramide en plan, , nous traçons les fuyantes d’arêtes de ce dernier!
Matérialisé en orange, nous découvrons les points de l’emboîtement fictif du second pied dans l'entaille du premier .
Nous traçons ensuite une ligne de sol parallèlement au premier pied, ainsi que une hauteur (ici 300 mm) perpendiculairement à cette dernière . (judicieusement, afin d’être placé à l'extérieur du dessin qui serait vite encombré)
6/ depuis tous les points de coupes et d'entaille, nous projetons des fuyantes vers le développement en vraie grandeur, puis nous traçons le pied entier développé.
7/ Nous traçons dans un premier temps, le second pied en plan, et aux intersections de fuyantes réciproques, nous traçons et matérialisons l'entaille du premier pied et la coupe de niveau du second.
8/ Nous traçons aux intersections réciproques des fuyantes, l'entaille sur le développement, puis nous projetons les génératrices de points sur deux largeur de face de pied tracées en amont .
Aux intersections réciproques, nous traçons enfin l'entaille vue de face et de coté, ainsi que les coupes au sol et de niveau.
Avec quelques ombrages et couleurs, nous matérialisons le tout .
Le tracé des bois se fait par rembarrement classique sur un pied, qui nous sert ensuite a tracer les trois autres.
Enfin il ne reste plus qu'à tailler et monter l'exercice .
ici un exercice présent sur l'air du bois :
Buenos aires sur plan carré, pieds section rectangle en devers
Ici nous découvrons que les codes du tracé de l'épure est similaire au précédent exercice, et que le secret réside sur le tracé de la vue par bout !
Avec des pieds de sections rectangulaire, on pourrait imaginer du chantournage par exemple !
Buenos aires sur plan carré, pieds section avec angle de corroyage et entailles choisies
Pour cet exercice, nous corroyons les bois avec l'angle dièdre, ce qui permet de choisir les profondeurs d'entailles (ici 10 mm) .
Nous pouvons aussi nous passer d'entaille afin que les bois se croisent sur leurs seules faces, pour cela la vue par bout sera tracée au ras de l’arête .
Buenos aires sur plan triangle équilatéral, pieds section carrée en devers
Le principe reste le même, sauf que pour un angle aigu à 60°, l'entaille est inversée car nous positionnons la vue par bout alignée avec l’arête extérieure !
Le tracé demande plus précision et de réflexion .
ici un exercice réalisé :
Guéridon à piétement Buenos aires sur plan carré, pieds section carrée en devers
Enfin pour finir, un projet concret à l'image de ce petit guéridon .
L'épure est classique, sauf que nous ajoutons des éléments comme le plateau !
Nous pouvons faire varier le tréteau en remontant ou en descendant le "noeud", ce qui resserre ou écarte le piétement (tout est possible) .
Tracé du premier pied depuis la vue par bout et l'emprunt !
Tracé du second pied et tracé de l'entaille !
Tracé du développement en vraie grandeur par projection des points.
Épure terminée et tracé par rembarrement des bois .
Voilà pour la découverte de ce principe d'assemblage en arêtier, je le redis tout est possible à condition de maîtriser cette première approche .
Je dessinerai plus tard d'autre projets à base de Buenos aire plus compliqués et aboutis, en attendant à vous de jouer ! 
ici un procédé d'épure en charpente : lairdubois.fr/..._comment_254282
ici de beaux exemples :
A suivre !
Ce pas à pas présente un projet en cours de réalisation.





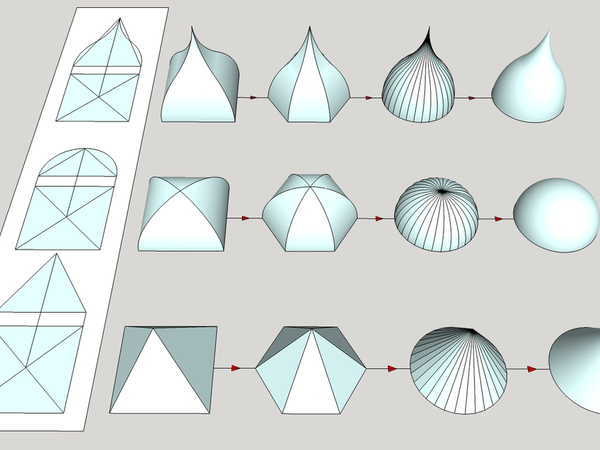
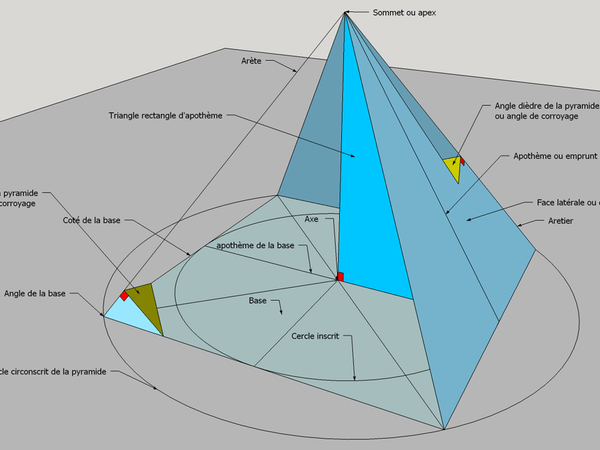
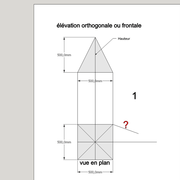
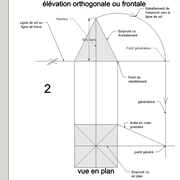
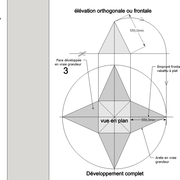
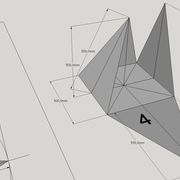
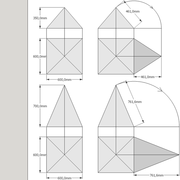
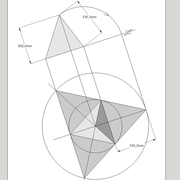
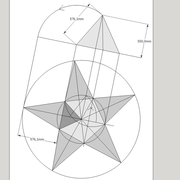
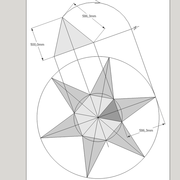
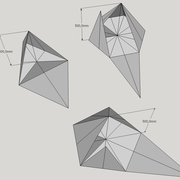
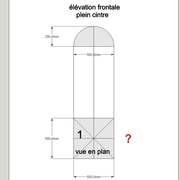
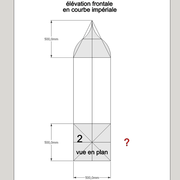
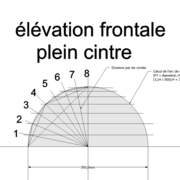
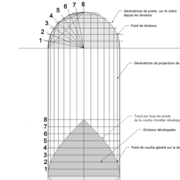

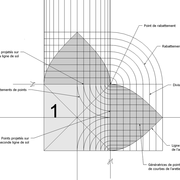
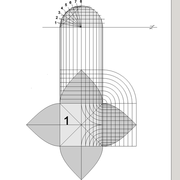
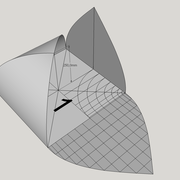
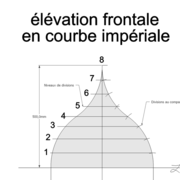
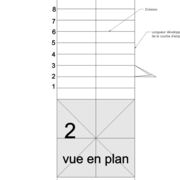
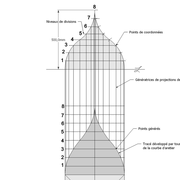
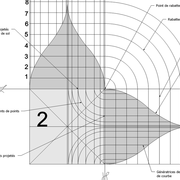
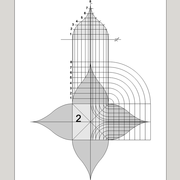
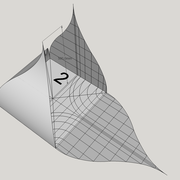
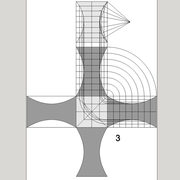


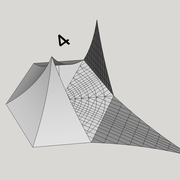
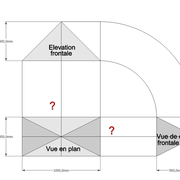
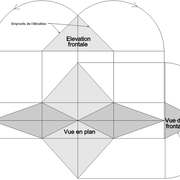
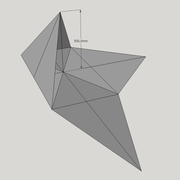
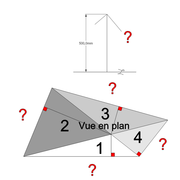
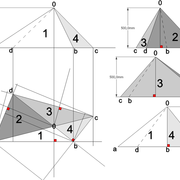
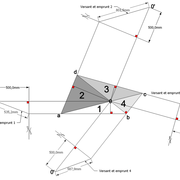
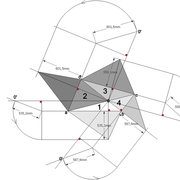
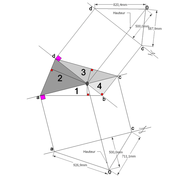
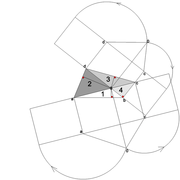
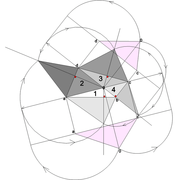
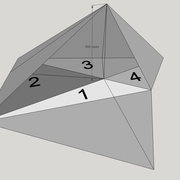
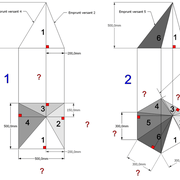
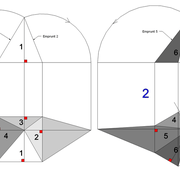
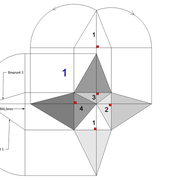
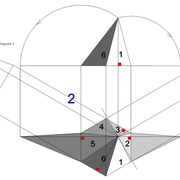
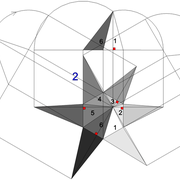
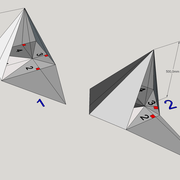
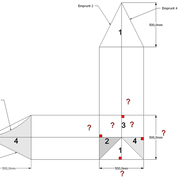
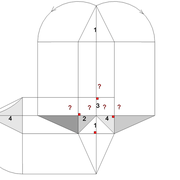
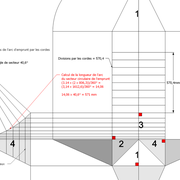
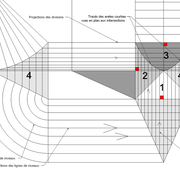
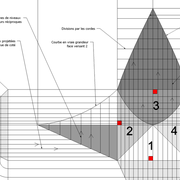
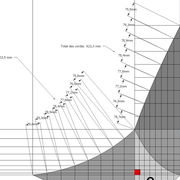
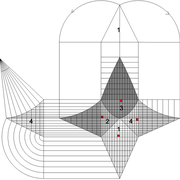
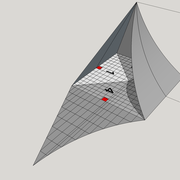
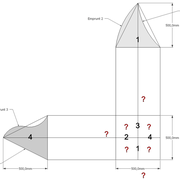
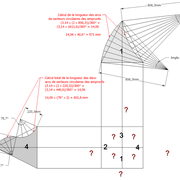
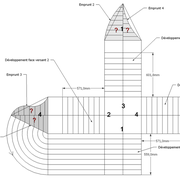
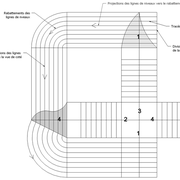
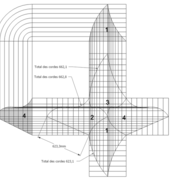
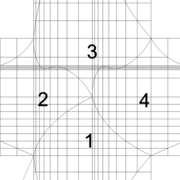
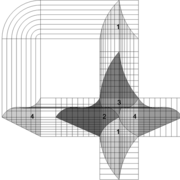
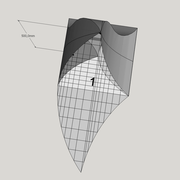
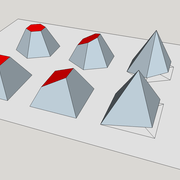
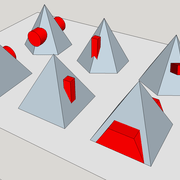
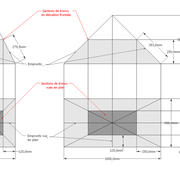
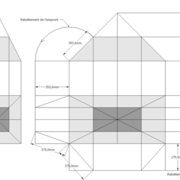
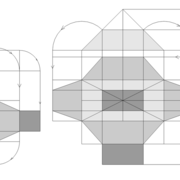
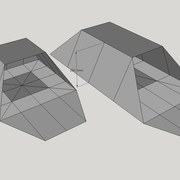
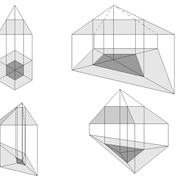
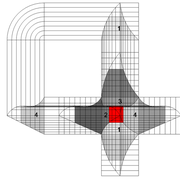
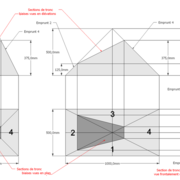
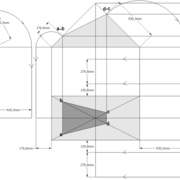
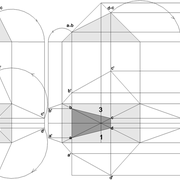
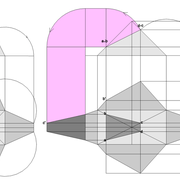
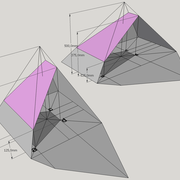
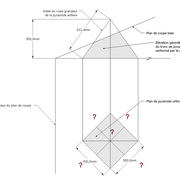
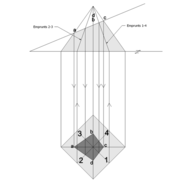
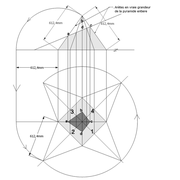
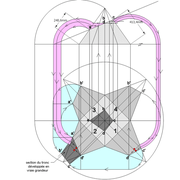
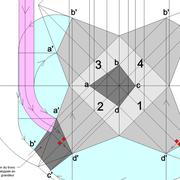
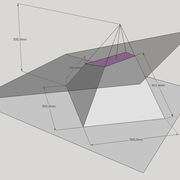
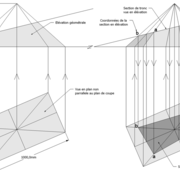
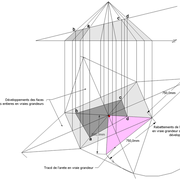
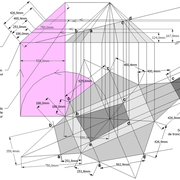
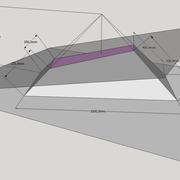
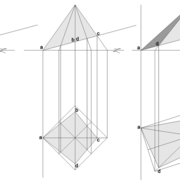
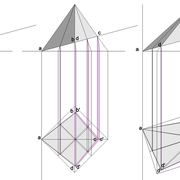
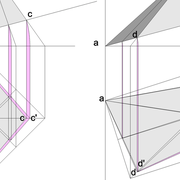
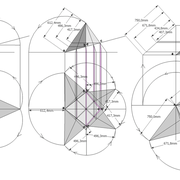
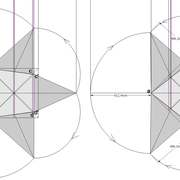
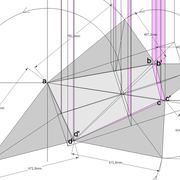
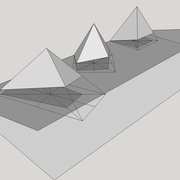
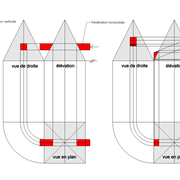
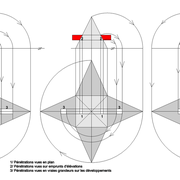
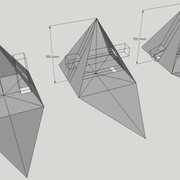
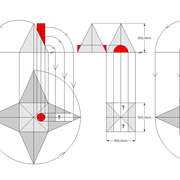
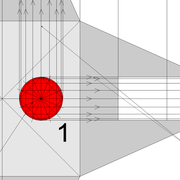
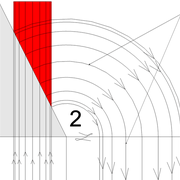
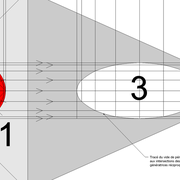
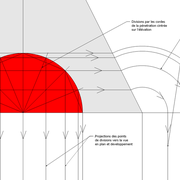
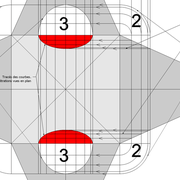
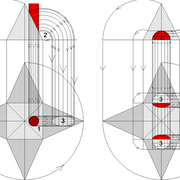
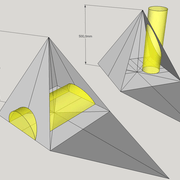
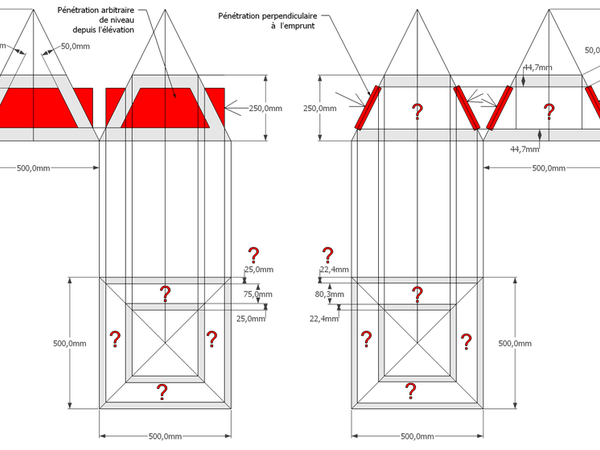
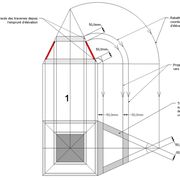
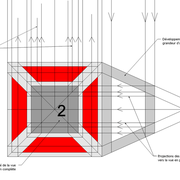
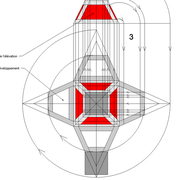
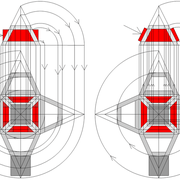
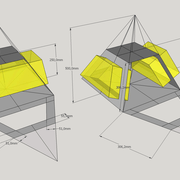
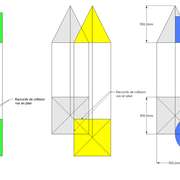
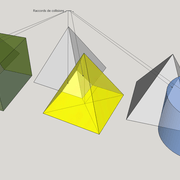
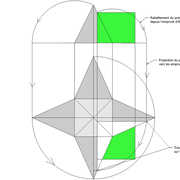
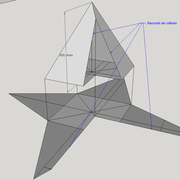
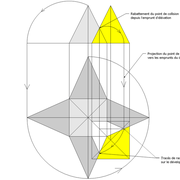
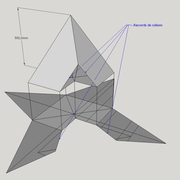
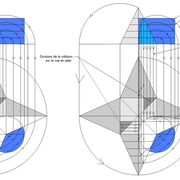
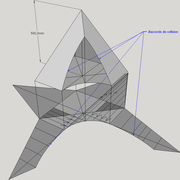
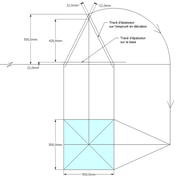
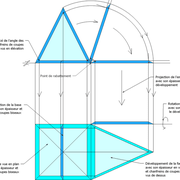
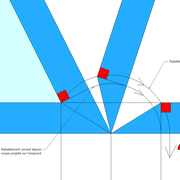
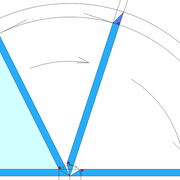
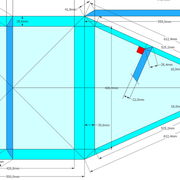
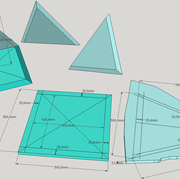
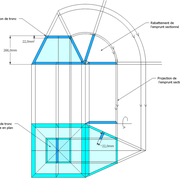
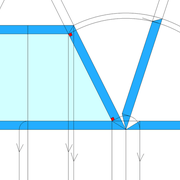
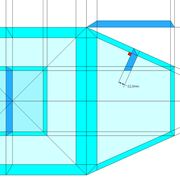
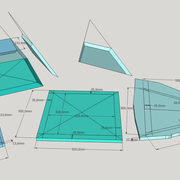
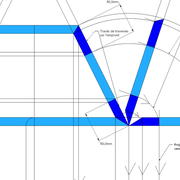
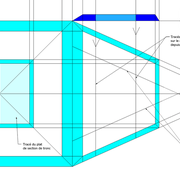
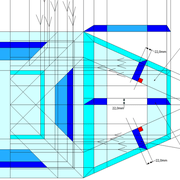
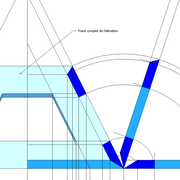
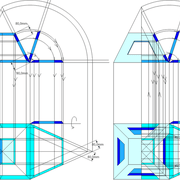
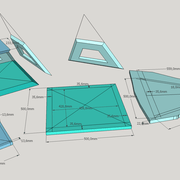
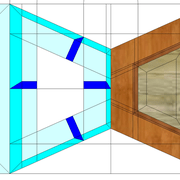
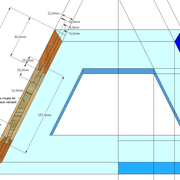
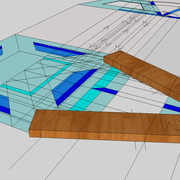

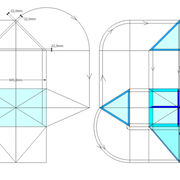
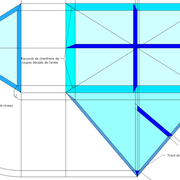
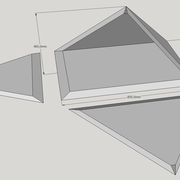
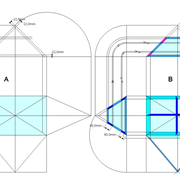
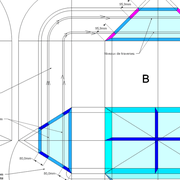
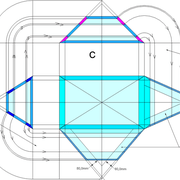
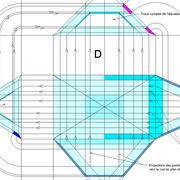
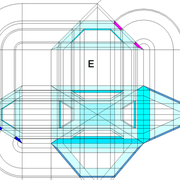
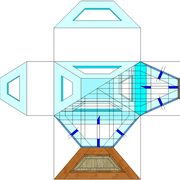
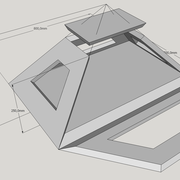
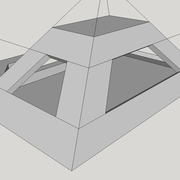
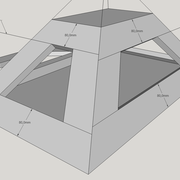
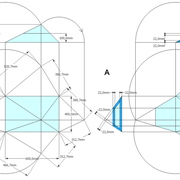
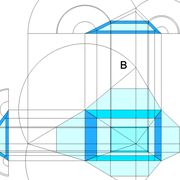
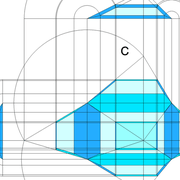
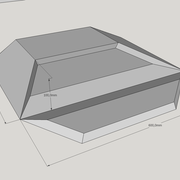
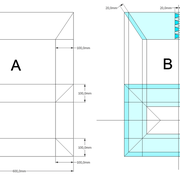
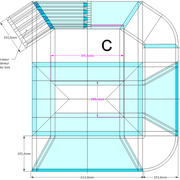
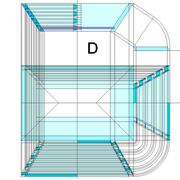

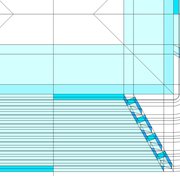

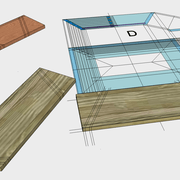



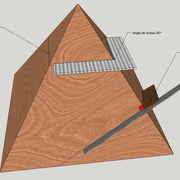
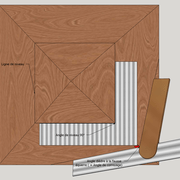
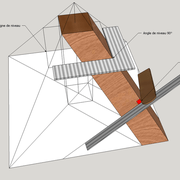
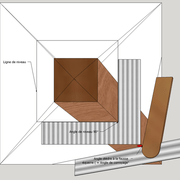
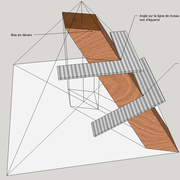
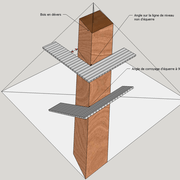
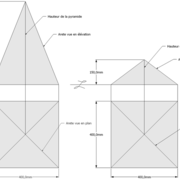
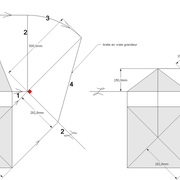
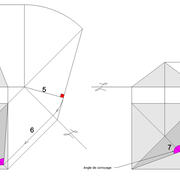
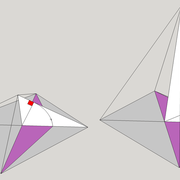
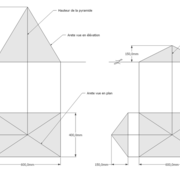
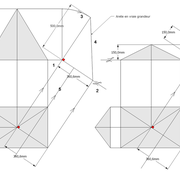
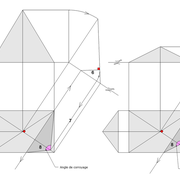
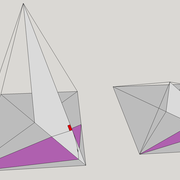
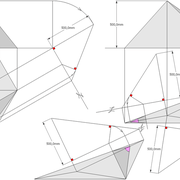
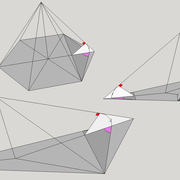
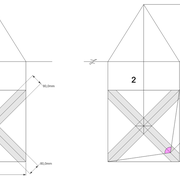
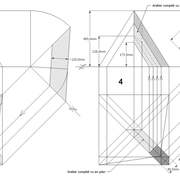
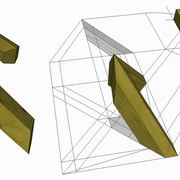
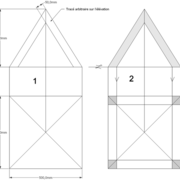
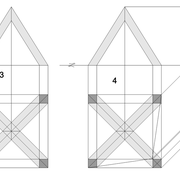
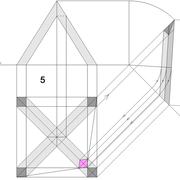
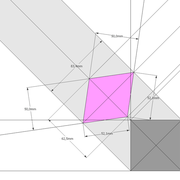
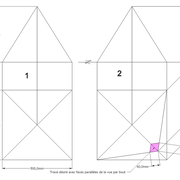
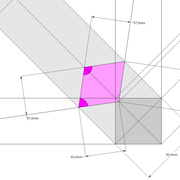
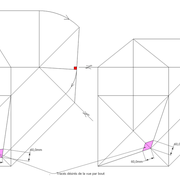
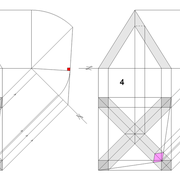
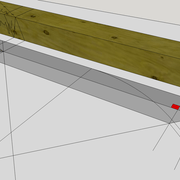
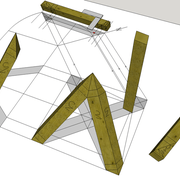
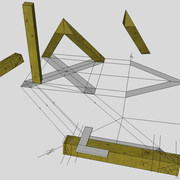
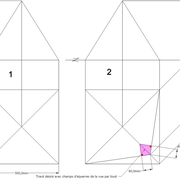
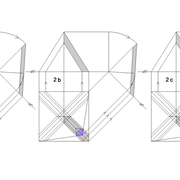
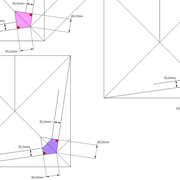
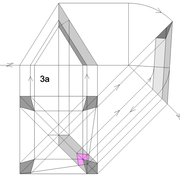
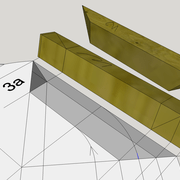
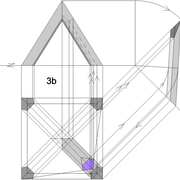
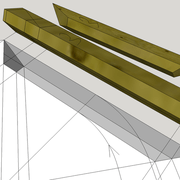
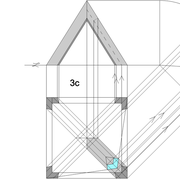
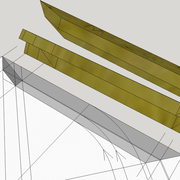
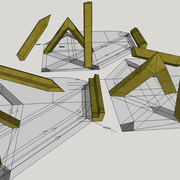
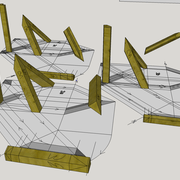
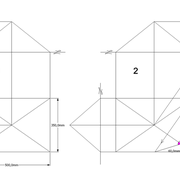
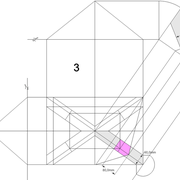
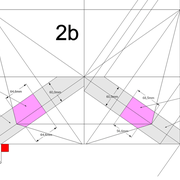
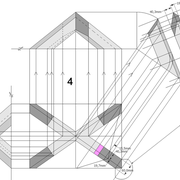
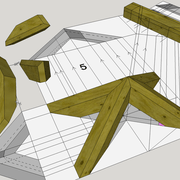

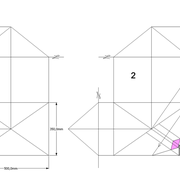
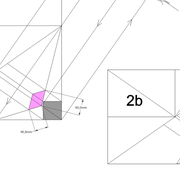
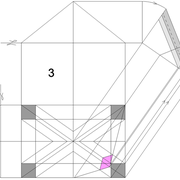
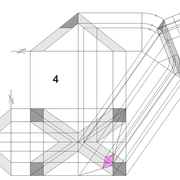

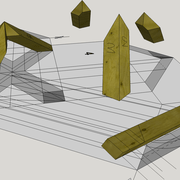

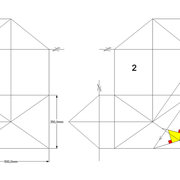
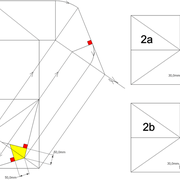
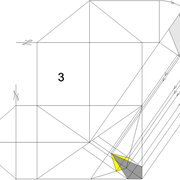
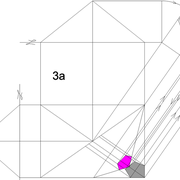
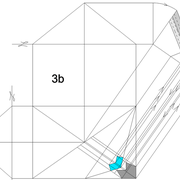
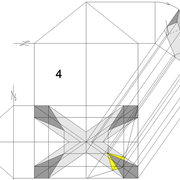
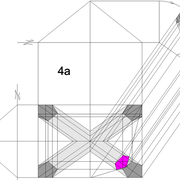
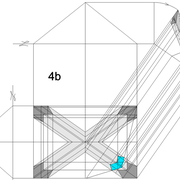
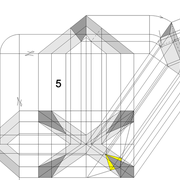
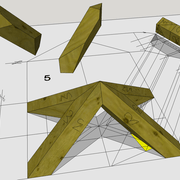
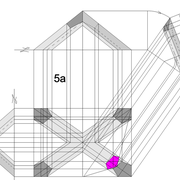
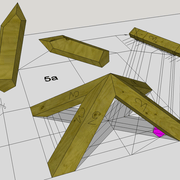
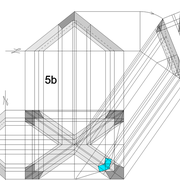
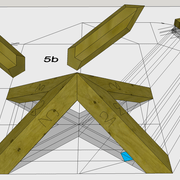

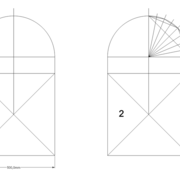
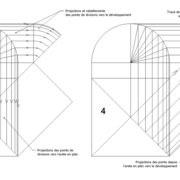
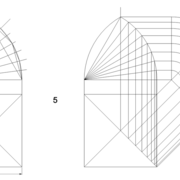
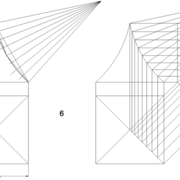
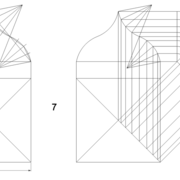
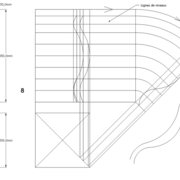
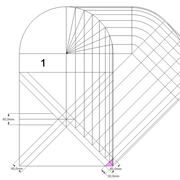
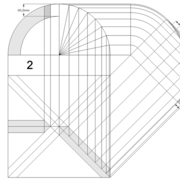
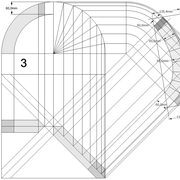
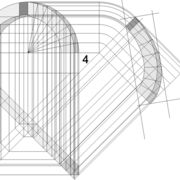


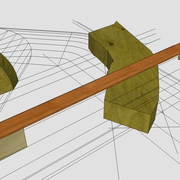
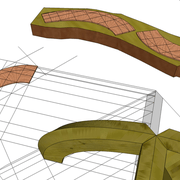
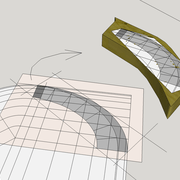

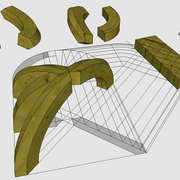
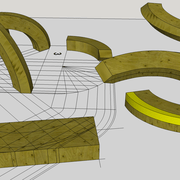

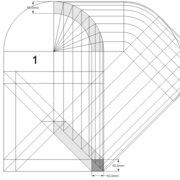
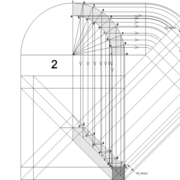
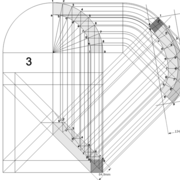
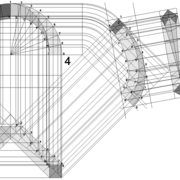
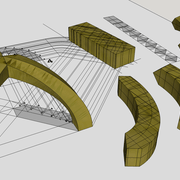
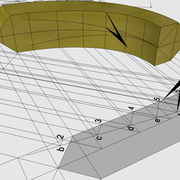


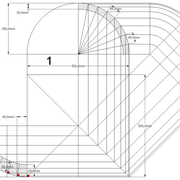
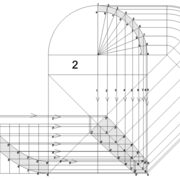
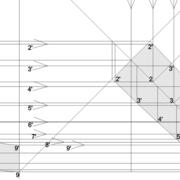
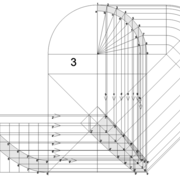
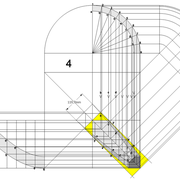
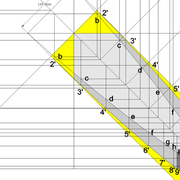
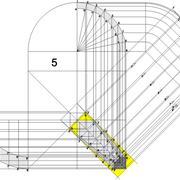
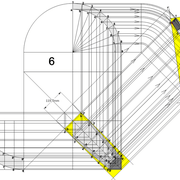
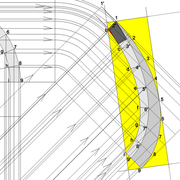
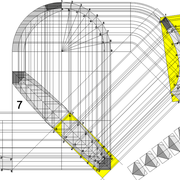
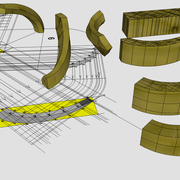
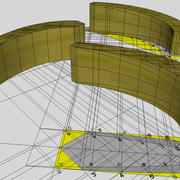



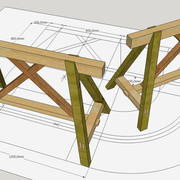

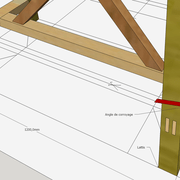
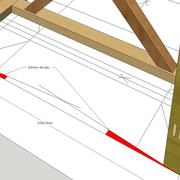
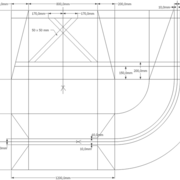
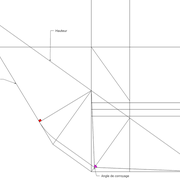
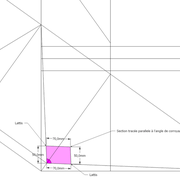
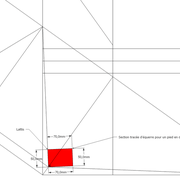
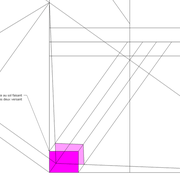
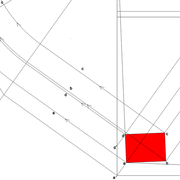
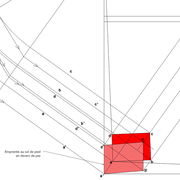
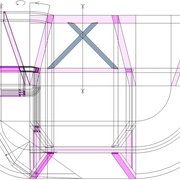
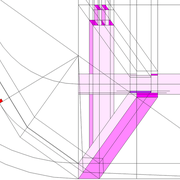
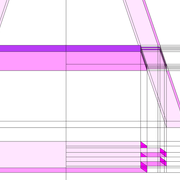
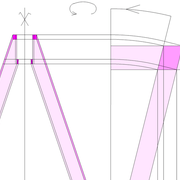
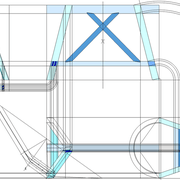
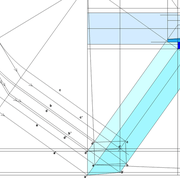
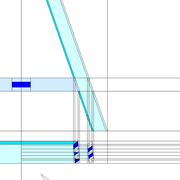
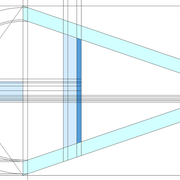
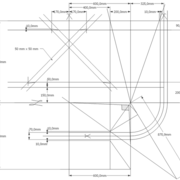
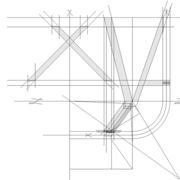
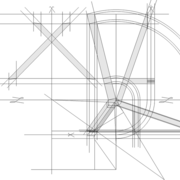
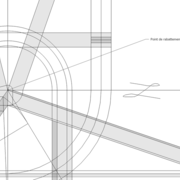
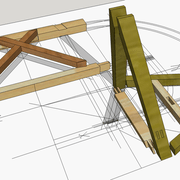
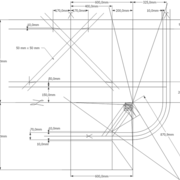
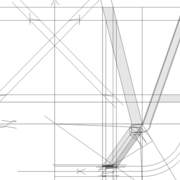
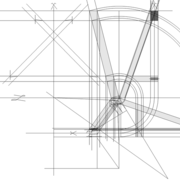
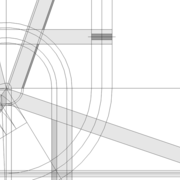
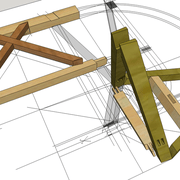
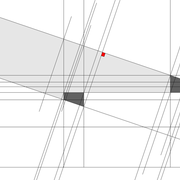
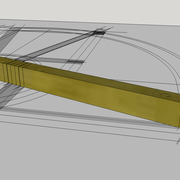
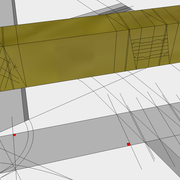
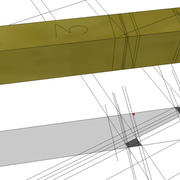
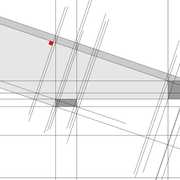
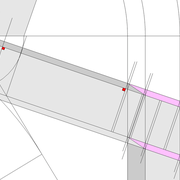
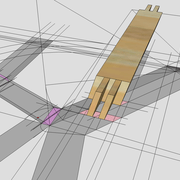

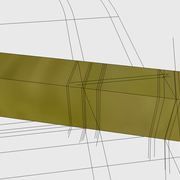

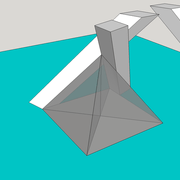

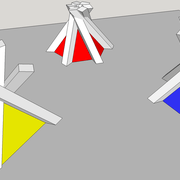
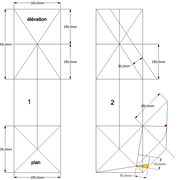
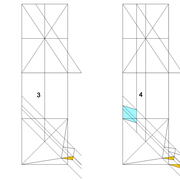
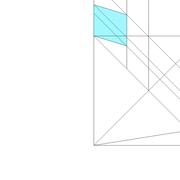
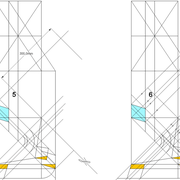
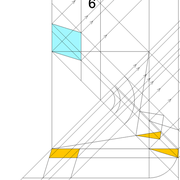
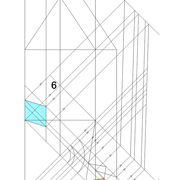
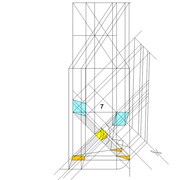
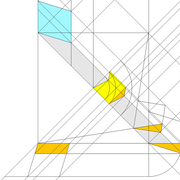
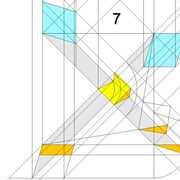
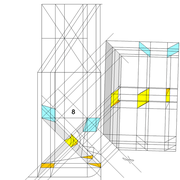
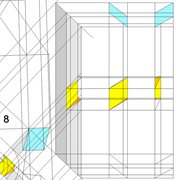
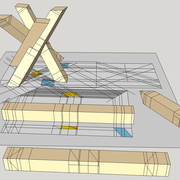
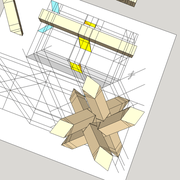
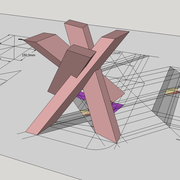
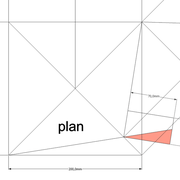
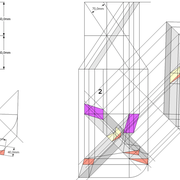
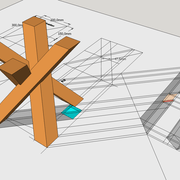
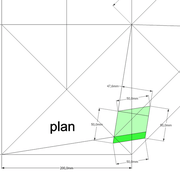
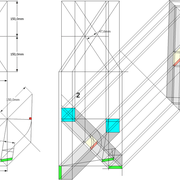
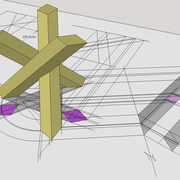
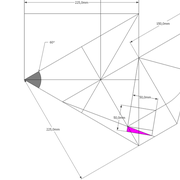
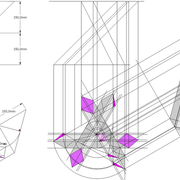
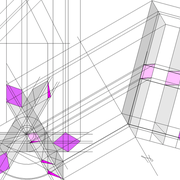



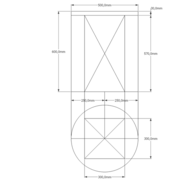
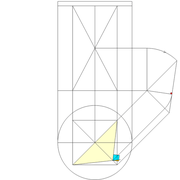
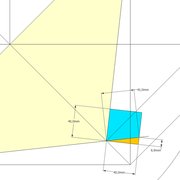
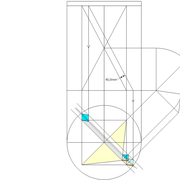
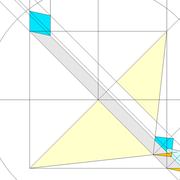
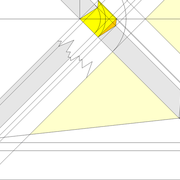
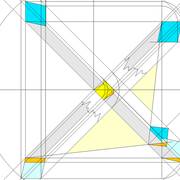
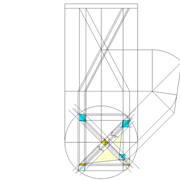
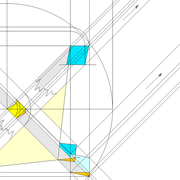
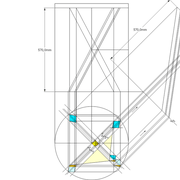
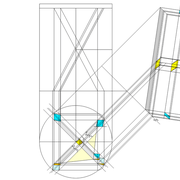
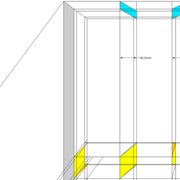
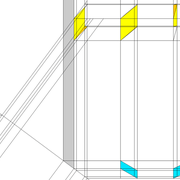
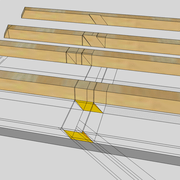
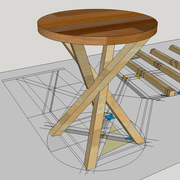





Discussions
Je sens que je vais avoir de la lecture... Merci par avance sylvainlefrancomtois !
oui ça commence maintenant !!
Merci.
de rien ,c'est que du plaisir pour moi !
Encore un pas à pas signé SYLVAIN, un pas à pas référence de plus, bientôt le livre chez BLB (je me suis renseigné à la source à Epinal). Ce pas à pas est dans la collection qui va bien!!!
J’espère que ça été très sympas ces rencontres !!
Très sympa, beaucoup de beau monde sur ce salon!
+1
Pour l'instant ça va, j'ai compris! ;) Merci, je sens que cela va être très très très intéressant!!
Ah, que voila une excellente initiative
Nous permettre enfin de comprendre les propos "ésotériques" de quelques participants (les lecteurs assidus le-les reconnaitront ) à ce forum qui prennent un malin plaisir à montrer aux pauvres ignorants que nous sommes que eux savent !
Encore merci pour cet esprit de partage, cela va me permettre de revoir mes vieilles notions de descriptive.
Encore un tres bel article, ou belle leçon sylvain.
Merci pour tout ce que tu nous apporte via l adb.
Le partage c est de rendre accessible a tous certaines choses qui paraissent trop compliquée sans acquis préalable et tu y parvient a merveille.
Je pense que la capacité a transmettre et aussi importante que le savoir pour faire un bon maître.
Merci encore maitre sylvain.
de rien
Génial! Merci pour ce partage !!!! Et merci de ta collaboration avec blb pour le hors série a venir !!! (Je croyais le trouver au salon, impatient que j'étais mais il faut savoir savourer son impatience !)
Génial !!! Pas encore lu mais je réagis d'avance.
On sait déjà qu'on va se régaler quand on voit le cuisinier mais je me garde de le déguster au bon moment !
Sylvain, génial, comme d'hab
Merci !
Jsuis comme un gamin devant sa serie et qui veux l episode suivant !!! je vais suivre avec attention pour enfin comprendre ce charabia !
qui m as pourtant bien l’air d un savoir ancestral de qualité ;)
Excellente initiative! Comme ça je me remettrais dans les tracés des menuisiers!
Oooh pu...n que c'est bon ça!. Moi qui ai du mal avec les termes . Merci sylvainlefrancomtois pour le temps passé.
. Merci sylvainlefrancomtois pour le temps passé.
Merci!
Merci de faire descendre « l’art du trait de charpente » de sa tour d’ivoire! Et de le rendre accessible au plus grand nombre par tes pas à pas! C’est l’idée que je me fait de cette plateforme!
Merci!
Pas faux aussi...
merci a tous !
Merci François pour ta démarche de partage.
Depuis ton arrivée ici, tu nous as montré que tu avais une grande connaissance théorique et pratique.Mais le fossé était grand et j'ai souvent butté sur la compréhension et la mise en pratique de la "géométrie" descriptive" et je dois dire que j'étais un peu frustré... mais toi aussi tu t'es amélioré en pédagogie pour notre plus grand plaisir. Je vais suivre tes articles avec intérêt et j'espère franchir un nouveau cap.
Merci pour cette passion partagée.
merci , mais sylvain c'est mieux !!
"Sylvain" et pas "François" merci
Mon nouveau livre de chevet numérique
Quel savoir! Quel amour du partage!
Merci sylvainlefrancomtois
Sylvain vous dites ceci ... :
"4/ En découpant notre construction , et en repliant le tout en un volume, nous obtenons une pyramide avec la base et sa hauteur désirée !!
Tout le principe approfondis de l’arêtier.... vers des travaux en COURBES les plus COMPLEXES... , découlerons de ce simple procédé à comprendre !"
Attention ! A ce genre d'affirmation.... Veuillez préciser votre pensée.
Cordialement.
pitié ,dis moi tu svp sinon Pas besoin de préciser car c'est vrais , et je vais le démontrer dans les prochains chapitres !
sinon Pas besoin de préciser car c'est vrais , et je vais le démontrer dans les prochains chapitres !
ou alors tu as pensé que j’allais m’arrêter là ? ou encore ais je mal formulé ?
JPA33 Peut-être faudrait-il laisser Sylvain développer de lui-même son propos qui n'en est qu'à l'introduction et qui essaie avec des mots et concepts simples, de se mettre à la place du type comme moi qui n'y connait pas grand chose. On peut supposer qu'il y a la une progression pédagogique. Suivons la, et il sera sans doute toujours temps ultérieurement de commenter et de discourir entre "Grands Sachants"... :)
Oui d'acord, je fais confiance à Sylvain pour le comment traiter son sujet,.... sans confusion... et avec quelques Epures simples.
A suivre,
JPA33 merci du retour ,c'est prévu plus tard , j'essaye d'inventer une méthode pour ne pas embrouiller les plus novices et applicables pas seulement en charpente !
Kentaro
Rares sont les pédagogues, qui savent transmettre un métier sans embrouiller les novices/élèves.
Merci Sylvain! vous êtes un des rares.
Au début le thème m'a un peu rebuté, mais j'y prend gout peu à peu. C'est la méthode Monge de dessin appliquée au bois. Superbe, deux choses qui me passionnent
ckarriere merci !
Super idée !
on attend avec impatience la suite !!
Génial, je dois faire des volumes en forme de pyramide pour un mur d escalade.... et voilà un cours qui tombe à pic
je n'aurais jamais pensé a ça , mais si tu y trouve ton compte !!
sylvainlefrancomtois Eh oui, il n'y a aucune exclusivité..... tout est possible, même dans certains Metiers !
Merci Sylvain. Bravo!
Tu relèves là un défi, vulgariser le trait comme disent les Charpentiers ou le traçage comme disent les chaudronniers ou les Fumistes. Chapeau!
merci racm
Trait.... Stérétomie..... Géométrie Descriptive (La Descro) sont, dans l'ordre 'd'ancienneté', l'Art, le Savoir naturel ou appris de la Vision dans l'Espace.......
Super et merci pour le partage. Moi qui ai galéré dans ma dernière réalisation - correspondant å une pyramide tronquée - pour calculer l'angle des arêtes å coup de formule trigo complexe, j'ai hâte de savoir comment j'aurai pu l'obtenir par tracé...
Sinon, il y a Une méthode "alternative" pour le calcul des angles des arêtes d'une pyramide ;)
Et la même chose pour une pyramide hexagonale, et desaxée:
JPA33 La trigo sphérique, oui, mais ce sont encore des formules un peu compliquées et on peut toujours faire une erreur. Avec l'outil vectoriel, produits scalaire, etc, on a quelque chose de bien plus puissant, extrêmement simple et presque automatique quand on en connait le fonctionnement.
JPA33 Non, il ne s'agit pas d'expérience ni de maîtrise, il suffit de savoir ce qu'est le calcul vectoriel (niveau terminale). Et de plus, ma feuille de calcul permet d'utiliser cette méthode dans pas mal de cas complexes sans avoir à comprendre le fonctionnement. Il suffit alors de rentrer les coordonnées xyz de 4 points.
Je rappelle ici que évidement tout peu se calculer ,et ne renie en rien les méthodes mathématiques !
La démarche d'apprendre l’arêtier dans nos professions par le trait d'épures est purement pratique , car elle permet de façonner des bois par positionnement, tirer des gabarit ,déplier des feuillets lamellés, etc ,etc .
Donc pour nous, même si nous l'apprenons , par la suite les calculs trigo et autres ont peu d’intérêts !
Exemple : calculer des longueur avec les angles qui vont avec ,pour une épure de charpente echelle 1 donnera du tracé aléatoire ,car les bois ne sont pas souvent qualibrés précisément voire bruts .
D'expérience , les jeunes à qui j'ai eu à faire en apprentissage , avait pour la plupart des craintes sur leurs capacités à découvrir l’arêtier "académique" teinté de formules et autres .
Ma démarche à toujours été de leur démontrer à la base la "facilité" par le tracé qui leurs permettaient ensuite d'aborder la théorie math de façon intégrable à du concret .
sylvainlefrancomtois Entièrement d'accord! :)
JPA33 J'ai donné les détails des calculs sur la page donnée en lien. Ma méthode permet en quelques minutes de calculer tous les angles d'une pyramide hexagonale, octogonale, etc, et désaxée quelconque. Mais chacun utilise la méthode qui lui convient le mieux :)
Ma feuille de calcul permet de calculer l'angle dièdre pour deux plans QUELCONQUES qui se rencontrent en formant une droite. Pour cela, il faut deux points sur la droite, et un point sur chacun des plans. Donc, TOUS les cas où on a deux surfaces planes qui se rencontrent, quelque soit l'orientation de ces surfaces.
Pour la rencontre de deux surfaces courbes quelconque, on peut également l'utiliser. Il faut dans ce cas former une succession de plans tangents aux deux surfaces courbes au niveau de la jonction.
JPA33 c'est un constat ! avec internet et autres tutos, il y à un lissage général navrant des fondamentaux !
JPA33 un exemple de pyramide hexagonale désaxée, que je me suis amusé à faire. Les calculs de tous les angles ont pris quelques minutes, le temps de rentrer les coordonnées des points sur la feuille de calcul.
JPA33 Si tu veux absolument avoir raison, pourquoi pas... ;)
C'est un cas particulier relativement général, sachant qu'il n'y a pas un coté pareil à l'autre, pas un angle semblable à l'autre, etc. On peut augmenter le nombre de
cotés autant que l'on veut, les rendre totalement irréguliers, et même définir une hauteur quasiment infinie, ce qui donne une colonne... ;) . Tout est possible... Donc, si tu veux absolument penser que c'est un cas particulier, ok, je te laisse le penser... :)
Maintenant, si tu as des cas particuliers qui n'entrent pas, penses-tu, dans ce cadre, je veux bien que tu me les donnes afin que je voie si je peux les traiter... :)
J'ai enfin compris l'intérêt du rabatement, qui restait obscurs pour moi. Merci!
Bravo pour le livre. Vivement qu'il sorte.
Attend la suite , tu vas en voir beaucoup des rabattements !
Encore une belle œuvre! Je vais finir par tuer mon ordinateur à force de vous lire.. en parlant de livre avez vous pensé à brocher tout ces traités?
Dis moi tu svp !! oui j'y ai pensé ! mais c'est pas si simple !
Ca doit faire au moins 10 fois que j'ai droit au "dis moi tu svp" ;)
Meme si ces traités la ne sont pas brochés, j'attend avec impatience le prochain hors série du bouvet!
Vincent Mathieu je l'ai reçu il y a 15j ! Que du bonheur...
Grabouille merci ;)
sylvainlefrancomtois de rien! je me régale...
C'est magique... :)
Ce qui est amusant, c'est que tu utilises un logiciel de dessin 3D pour tracer tout cela! ;)
Pour mémoire , on peut faire les tracés 2D sur logiciel , puis les imprimer avant de découper les exercices !
Mais il faut évidement savoir tracer à la main ,pour une épure ech 1 ,donc s'exercer sur papier à petite échelle est préférable au départ .
c'est magnifique de beauté mathématique, les seules que j'aime! merci à toi!
merci Marie Anne !
Oula, j'ai pas encore lu, mais j'ai le sentiment que ça se corse déjà !
Très intéressant et bien expliqué, grand merci!
J'ai tout de même une question pratique dans le grand A du Développement d'une face du dôme de pyramide en courbe
comment est trouvée la longueur des huit segments réguliers ? est-ce par tâtonnement (essais jusqu'à trouver la bonne longeur) ? ou y a t-il une autre technique ?
Hello ici c'est par tâtonnements (ca vas encore assez vite) , sinon dans des épures echelle 1 ,on peut parfois mesurer avec un grand réglet souple que l'on plie ,calculer ,puis tracer les segments (il faut parfois être à deux , ou mettre des pointes)
Merci Sylvain de ce rappel très clair des bases du trait, la vulgarisation est un art! ça donne envie de racheter de la carte blanche et de faire quelques pliages!
faut pas se gêner !! cela remet immédiatement la machine en route ,moi le premier
De la carte blanche... ou du zinc!;)
oui tout ce qui est pliable !
Excellent, j'attends la suite avec impatience, même si je suis parfois obligé de lire 10 fois pour comprendre .
.
Bravo et Merci
le secret , est de tracer et faire les exercice en plus de la lecture !
Ça y est ! Il faut déjà un peu plus de temps pour lire et comprendre en même temps.
L'emprunt c'est la hauteur du triangle déterminé par la face de la pyramide ?
Par contre, le terme "emprunt" reste valable même si la face n'est pas un triangle j'imagine ?
Ce qui est intéressant, c'est que ton approche est différente de celles que j'ai pu voir par ailleurs. Et la cerise sur le gâteau, c'est que l’auteur est disponible en cas de besoin. (un grand merci d'ailleurs pour ta disponibilité).
"Le Chevron d'Emprunt d'une Surface Plane inclinée est une Ligne de Pente Rectiligne de ce Plan et tj perpendiculaire à une Droite Horizontale de ce Plan"..... Donc pas forcément du Sommet.
Pour tous autres types de Surfaces, Réglées par des Horizontales //es entre elles (Pour en rester là), il faut y ajouter d'autres Conditions Géométriques selon.
Pour apprécier le texte ci-dessus, faites manuellement une Epure simplifiée d'un Exemple minimal très simple, avec Projections Vert., Frontale et un Profil..... et en repérant les Termes de la Définition ci-dessus.
JPA33 oui merci, j'en ai fait quelques unes déjà. Mais dans les "20 leçons" le terme d'"emprunt"n'est pas utilisé (ni apothème d'ailleurs). Du coup, je voulais vérifier si ça correspondait à un synonyme déjà vu.
JPA33 "Le Chevron d'Emprunt d'une Surface Plane inclinée est une Ligne de Pente Rectiligne de ce Plan et tj perpendiculaire à une Droite Horizontale de ce Plan"..... Donc pas forcément du Sommet.
oui tu as raison , mais pour l'instant je garde au maximum l'apex pour ne perdre personne
sylvainlefrancomtois Ce que je trouve intéressant dans ton approche didactique, c'est que justement tu ne t'accroches pas aux termes parfois fort ésotériques, issus d'une langue venue des tréfonds du fin fond du moyen-âge...
Il vaut mieux se focaliser sur les principes, la méthode.
Les termes utilisés, propres au métier, c'est pour moi secondaire. C'est un peu comme pour construire un bateau. Il y a 100 termes que les spécialistes se gardent jalousement entre eux, pour se faire croire qu'ils "savent" et qu'ils existent. Mais ce qui est important, c'est la méthode. Et quand on a compris la méthode, on a tout compris.
chevron d'emprunt = ligne de plus grande pente .
non , l'emprunt , c'est toujours le profil du coté d'un pyramidal vu en élévation frontale ,et en plan il est toujours perpendiculaire à la base depuis l'apex vu en plan (apothème)!! la hauteur reste toujours la hauteur en verticale d'aplomb de l'apex (sommet) vers la base . vois tu ?
C'est vrais que dans l'élévation frontale de pyramide classique l'emprunt vu de face peut être confondu avec la hauteur !! je vais le notifier !
Sinon oui j'essaye d'inventer une autre approche ,que j'aurais aimée avoir en d'autre temps
Ah merci, en fait j'ai raison en réfléchissant en 2D sur une frontale. Mais ce qui nous intéresse c'est la 3D ;)
trente six seb oui puisque nous somme dans de la géométrie dans l'espace !
Oui puis faire des meubles juste avec du placage... bof quoi, la 3D c'est mieux
(même si on n'a pas commencé à traiter des épaisseurs)
Mais non c'est pas de l'origami !!!!
C'est un super cours en ligne !
Merci Sylvain ! On s'accroche !
Génial !!!! merci du retour ! tu verras après en passant au bois ,des automatismes seront là
Très bonne initiatique classique !
Une idée sur votre lancée : Faites tous les types de Trièdres possibles, sur le même principe.
Mais, je vous l'assure, vous aurez besoin de faire des Epures papier, à l'Echelle que vous voulez.... puis pliages, collage des rabats et report sur les faces des Données Graphiques à partir des Epures.
Déjà fait avec des Jeunes en Apprentissage.
JPA33 en plus çà fait réviser le comment faire les pentagone et autres gones et ièdres ! et surtout arriver à prendre le bon format papier ou tracer au bon endroit sur la feuille pour ne pas tracer sur le bureau !!!!!


sylvainlefrancomtois celui là je vais le suivre au fur et à mesure sinon c'est dur de s'y mettre après !!!
dependancesbois oui c'est l'avantage, c'est plus digeste qu'un gros pavé d'un seul tenant. Autant profiter des publications ponctuelles.
dependancesbois
trente six seb
sylvainlefrancomtois Si je comprends bien, pour la division de l'emprunt de la courbe impériale en vue frontale , tu as obtenu les 8 segments par tâtonnement et ensuite tu as gardé le même écartement du compas pour les divisions en vue en plan ?
Et division par les cordes pour les autres formes?
oui c'est cela !
Sinon dès que tu as accès à une courbe tracée a partir de coups de compas ,par le rayon on calcule ! ex un impériale "régulier" (même rayon et même longueur pour le cintre convexe et concave ,que l'on peut diviser par cordes pour tracer les divisions d'emprunt
Pas clair du tout votre demande !
Si en Projection Frontale vous avez une Courbe Impériale comme Emprunt, divisée au compas en segments égaux, en Projection Horizontale vous n'aurez pas de Segments égaux !!
A moi, cela me semble plutôt clair... Si j'ai bien compris, on divise la longueur de la courbe en segments égaux et on divise cette courbe en 8, en longeant la courbe. Cela ne donne pas des divisions égales sur le plan du haut, mais sur le plan du bas, elles sont par principes égales et c'est justement ce qui donne la bonne "déformation" de la forme.
Kentaro +1
JPA33 si , car c'est l'emprunt que l'on redresse en ligne droite !
sylvainlefrancomtois
J'ai l'impression qu'on ne parle pas de la même chose, et que l'on confond tout,.... alors SVP, un simple croquis manuel annoté comme image.
JPA33 voilà ! on pourrait éventuellement dire que les cordes (écartement de compas) sont plus courtes que les petits segments de courbes ,'c'est vrais ,mais la différence tellement tenue que cela n'a pas d'incidence sur les travaux !
Perso ,quand mes écartements de compas successifs arrivaient genre 3/4 mm plus fort au final , je laissais en l'état cela rattrapais la différence !
Dans la réalité ,ex charpente , on se met à deux et on mesure au mètre pliant déployé ou une latte souple ,que l'on cintre le long de la courbe pour la mesurer !
sylvainlefrancomtois super merci Sylvain .
Je préférais m'ôter le doute.
merci Kentaro c'est plus clair que ce que je disais !
dependancesbois comme je le dit , il faut un assez grand nombre de divisions pour rester précis , mais pas trop pour rester clair !
Essaye avec 16 divisions contre huit , tu verras que les courbes développées au final se superposent !
sylvainlefrancomtois je le ferais ! Pour le coup mes dessins étant tout petit (50mm je profite de mon stock de feuille de brouillon) ça prêtait a confusion.
Pendant l'avancée de ton pas a pas j'essaierai d'aller vers un projet a une échelle plus parlante. Bien assimiler la chose d'abord car comme disais l'autre " j'comprends vite, mais faut m'expliquer longtemps "
Merci encore pour le temps que tu prends a vulgariser la chose.
tu comprendra tout quand on passera au bois !
J ai commencé à lire ton pas à pas avec attention balèze j avoue ne pas tout comprendre en tous cas bravo pour ce cour magistrale
Palissandre j'essaye de trouver une nouvelle technique ludique pour apprendre l’arêtier ,en passant par la pyramide "scolaire" tracée sur papier à découper !
Les tracés étant plat et développés pour l'instant , permettront de se familiariser en créant des automatismes , qui faciliteront les techniques pratiques futures sur des projet en bois !
sylvainlefrancomtois pas sur de me servir de tout ça en pratique mais ces génial de découvrir tous ca
Palissandre si un jour ,on te demande un présentoir design biais ou à faces courbes ,tu seras content de savoir ;)
sylvainlefrancomtois oui pour ça faut que j arrête de poser de la fenêtre et du vr à tous vas d ou l idée de me lancer d ici quelques années quand les enfants auront grandi un poil plus ça vas moins je supporte la pose et j espère bien me servir de ces cour
sylvainlefrancomtois, avant de me former en charpente, je me suis formé en couverture/zinguerie, parceque j’estimais obligatoire de me former en priorité ds ce que je faisais ts les jours ds la boite où je travaillais alors. Dans cette formation on voit les bases du dessin mais aussi les dévellopés, pour le travail du zinc notamment. Pyramides, cones etc...
Quand enfin j’ai pu “partir” en charpente, ce petit bagage a été d’une grande utilité pour apréander le trait de charpente!
Bref, le passage par le traçace de “pyramide scolaire” me semble trés judicieux de ta part.
Boisbarbu merci
En fait, je crois avoir compris la différence entre l'art du trait et le dessin industriel tel que je l'ai (un peu) appris à l'école. Le dessin industriel travaille par projection (on met une lampe devant l'objet, et on dessine ce qui est projeté sur un écran de face, de coté, de haut), alors que l'art du trait pratique par développement, par "dépliage" de formes. C'est beaucoup plus puissant...
Tu as les deux dans le trait et dans la conception industrielle (tôles, ...).
oui c'est cela , des vues orthogonales projetées permettent de visualiser en trois dimensions par faces planes à construire !
Le trait permet d'avoir des dessins de fabrication ou de représentation 3D (ancêtre de sketchu) de pièces ou d"éléments droits ou courbes ,non définis dans un plan orthogonale de projection !
Glorfindelrb +1 la géométrie descriptive (le trait ) découle obligatoirement des vues projetées orthogonalement !
par "dépliage" de formes. C'est beaucoup plus puissant... oui et sans limites de formes !!
sylvainlefrancomtois
Oui...... mais obligatoirement non.
Le/les Plan(s) de Projection(s) peut(vent) être incliné(s) dans le Référentiel Orthogonal choisi.
Les Lignes de Rappel étant, en principe, Perpendiculaires au Plan de Projection.
Pour une initiation, ou un rappel d'un apprentissage lointain, à suivre votre méthode que j'approuve.
le développement ou dépliage est une étape pour obtenir l'élévation ou projection de la pièce en vrai grandeur. Avec deux vues on en obtient une troisième.
JPA33 je pense que nous n'avons pas le même discour et finalité d'usage ! pour moi un changement de plan de projection (dusse t'il être purement pratique) nous sert à faire du dessin géométral cette fois ci !mais découle bien lui aussi de deux vues (le plan et l'élévation par exemple ) .
Oui.... mais cet pour être moins restrictif. Les plans de Projections ne sont pas forcément orthogonaux.
Une projection, sur n'importe quel plan, reste une "radiographie", un truc qui passe "au travers des choses". Ici, dans ce que nous montre Sylvain, on se balade sur la surface des choses. C'est ce qui est intéressant!
Sinon, pour calculer des développées, il y a la technique de triangulation d'une surface. C'est d'ailleurs ce qui est utilisé par les logiciels qui calculent le dessin des bordés d'une coque de bateau. Mais avant l'ordinateur, il y avait des gens qui dessinaient et calculaient tous les triangles...
Kentaro et après , ou va y mettre de l’épaisseur de matière et finaliser par de la taille ! c'est encore plus passionnant ! mais on n est pas rendu !
rendu !
Bravo Sylvain!
Aucune ambiguïté. C'est clair et net. Un réel plaisir de se laisser guider et de rêver à tout ce qui a été et qui sera réalisé grâce à ce savoir
Merci.
merci du retour ça fait plaisir , d'ailleurs le futur hors série du bouvet de découverte sur le trait sera dans ce style ! pourvus que cela plaise autant !
That is the question ?.... mais oui il y a des personnes qui apprecierons.... moi le premier et peut-être qu'on en reparlera.
Ouh la... ;)
Tu as oublié la pyramide à base quadrilatère quelconque et 4 faces courbes... ;)
et en plus à base biaise et hauteur décalée à l’extérieur de la vue en plan !!!
!!!
sylvainlefrancomtois Tant que ce sont des Versants Développables... au Sommet désaxé ou pas, avec Base biaisés ou pas, le problème global est le même ...... mais c'est une bonne progression.
Une petite chose... le vocabulaire... c'est ce qui me gène le plus. C'est du français, mais toujours un peu "voilé", détourné, vrillé...
Pourquoi "versant" ? "emprunt" ? "base biaise" ? sur la méthode, pas de problème, mais sur le vocabulaire, cela devient déjà ésotérique...
Serait-il possible d'apprendre les bases de l'art du trait sans avoir à apprendre aussi le vocabulaire spécifique ?
C'est un peu comme quand on fait du bateau... il y a un qui crie soudain "souque!! souque!! " et on se demande ce qu'il veut bien dire... il faut tirer ou bien lâcher la corde ? j'ai oublié, je panique... et plouf...
tu prends la seringue et l'aiguille , tu pose un garrot et tu peux faire ton intraveineuse ! tout le monde comprend !
Tu prend la petite pompe en plastique avec un bout pointu en métal ,tu entoures le bras avec l’élastique et tu piques dans la partie ou il faut piquer !
moi je veux bien ,mais il faut quand même garder les fondamentaux de chaque profession , appeler un chat un chat ,c'est rester clair et d'expliquer le pourquoi du comment ,je pense ! non ?
partager ce que l'on sait est un devoir , préserver ce qui est ancestral aussi ! nous sommes des passeurs ,essayons de faire aussi bien que nos anciens .
nous sommes des passeurs ,essayons de faire aussi bien que nos anciens .
Kentaro il faut bien appeler 'un Chat' par 'un Chat' ! Le vocabulaire, surtout Technique, et selon le Métier doit aussi s'apprendre pour se faire comprendre..... Si pour vous c'est 'difficile', pour nous aussi c'est difficile de comprendre ce que veut dire un Apprenant.... vous et les jeunes.
'Versant' = Surface inclinée où le Goutre d'eau suit la + Grande Pente.
'Emprunt' disont le 'Chevron d'Emprunt' = Ligne réelle, ou imaginaire, d'un Versant en Pente, Perpendiculaire à une Horizontale du Versant, ou à la Base du dit Versant, si elle est horizontale.
C'est aussi le support 'Lattis' (Dessus des Chevrons) dans un Plan de Profil du dit Versant et prêt à recevoir le complexe Couverture.
Le vocabulaire Charpente, entre autres, est très riche.....
JPA33 je suis un "vieux", moi aussi ;) c'est pour cela que j'ai un peu de mal à apprendre une nouvelle langue à mon âge... ;)
Oui, je sais, le langage technique est précieux, car il dénomme précisément les choses et permet de se comprendre ... entre comprenants... sauf que les non comprenants n'y comprennent rien. ;) ;) ;)
Et c'est aussi une bonne méthode pour souder les "comprenants" entre eux, et repousser les autres.
Donc, tu as mis des années à l'apprendre, ce vocabulaire, tu le maîtrises, c'est très bien, mais maintenant, il faut se mette à la place de ceux qui ne vont pas passer des années à l'apprendre, et qui veulent comprendre quand même...
Par exemple, tes définitions, c'est très poétique, c'est joli, mais je n'y ai rien compris... C'est quoi le Goutre d'eau ? et l'horizontale du Versant ? et le "complexe couverture " ? bref, c'est joli, mais en plus, la plupart des mots sont des mots du vocabulaire actuel, mais avec une acception ancienne ou détournée...
sylvainlefrancomtois Désolé, mais s'il faut apprendre une nouvelle langue pour comprendre "l'Art du trait", je suis trop vieux pour cela... ;) Mais pas de problème pour comprendre les principes :)
Kentaro
Il faut lire "Goutte d'eau".... mes excuses.
'Horizontales du Versant' :
Là, excusez-moi, c'est de la Géométrie Descriptive dans L'Espace..... je pense que si vous voulez comprendre comme il faut, la 'derniere fournée' de Sylvain, il va falloir vous y mettre sérieusement, avant d'être 'largué. Ce n'est pas ce qu'il veut faire, mais vous n'avez pas beaucoup le choix. Il y a un minimun...
Il est aussi nécessaire de se dire que nous sommes ici sur de la théorie pure supportée, ni par un geste, ni par des expressions de visage, ni par une action comme en atelier ou sur un chantier.
Ces termes sont plus facile à acquérir sur le terrain ou face professeur. L'exercice est infiniment difficile pour sylvainlefrancomtois qui s:en sort à merveille.
Ne rentrons pas dans l'élitisme, mais effectivement la charpente ne se réinventera pas ici. Alors il faut être précis.
Oak Entièrement d'accord, pas facile d'être pédagogique sur un écran, alors qu'un simple doigt sur une maquette indiquerait tout de suite de quoi il s'agit.
Mon propos était simplement de dire: attention, il doit être possible d'être pédagogique sans avoir nécessairement recours au langage ésotérique qui "enfume" les techniques anciennes comme l'art du trait.
Et je ne crois pas au discours "si tu veux apprendre la technique, petit, faut apprendre le vocabulaire!". Je n'y crois pas. Ce n'est qu'un truc pour compliquer les choses et asseoir le pouvoir des "maîtres" sur les apprentis...
JPA33 La pédagogie, c'est savoir se mettre au niveau de celui qui apprend. Ce n'est pas demander à celui qui apprend de se mettre au niveau du "maître".
(Pour ce qui est de la "goutte d'eau", ben, j'imagine une goutte d'eau qui suit une pente", mais cela ne me dit pas grand chose de plus sur la notion de "versant"... ;) )
Faites une visite dans les Centres de Formations pendant un cours en Salles et en Ateliers.
Vous verrez que le vocabulaire basique est toujours expliqué.
Il existe/ait aussi un dictionnaire des mots technique du Bâtiment.
JPA33 +1
Kentaro Je sais c'est pas simple pour le novice ! j'ai essayé de synthétiser au max ,mais il y a des limites !
Exemple : j'utilise les mots face versant chaque fois , pour que le novice se familiarise avec une face mais en pente du fait de 'l’arêtier en lui même sans changer l'idée dans le vocabulaire pro . Alors que les charpentiers disent versant (de toiture) , les faces biaises ou en trémie disent les menuisiers , et les parements galbés et autres chez les ébénistes , etc etc
Kentaro Si tu imagines un versant de toiture, la goutte d'eau venant du sommet prendra comme trajectoire l'emprunt (apothème) (elle emprunte théoriquement une ligne droite parfaitement perpendiculaire au chenaux (égout (égouttoir) pour le charpentiers)
sylvainlefrancomtois ok , merci!
sylvainlefrancomtois Je sais bien que tu essaies de simplifier, et on t'en remercie grandement ! :)
JPA33 oui, bien sur que dans un centre de formation pour professionnel, on apprend les termes qui vont permettre aux pros de communiquer entre eux. Mais ici, on n'est pas dans un centre de formation pour professionnels... ;)
(et puis, dans un centre de formation, apprendre des mots aux gamins, cela leur fait croire qu'ils apprennent quelque chose, c'est plus simple pour le formateur... ;) ).
Kentaro ton esprit rebelle remets en question les méthodes d'apprentissage mais pas le contenu je pense.
Si l'on te justifiait l'utilisation de chaque mot avec son histoire, si l'on te donnait en plus du super cours de charpente un super cours d'étymologie et d'histoire, je pense que cela te ferais sens.
Ah oui, tout à fait... :) ...
Kentaro a plus qu'à trouver un linguiste et un historien.... nous vla bien.
Kentaro Gamins de 15 à 25 ans !!!!... Ils vont être très contents...
JPA33 Je pratique assez souvent l'ironie... ;)
Oak Il y en a un ici , maître etiennedesthuillier qui à revisité tout le dialecte boiseux !
sylvainlefrancomtois et se fait un malin plaisir de ne pas ponctuer ses phrases, afin de laisser aux boiseux l'oreille d'entendre ses jeux de mots..
Pour le chevron d'emprunt pourquoi ne pas parler de ligne de plus grande pente, qu'on peut visualiser si on attache une bille à une ficelle et qu'on la laisse rouler librement elle se stabilisera sur cette ligne de plus grande pente.
Oui, c'est ce sui se fait sur chantier en charpente/comble existant, surtout par un Couvreur en Ardoise ou Tuiles plates.
Mais attention, car on rentre dans le domaine des "Lignes d'Ecoulements"...... et, pour nous, ce n'est valable que si : La vitesse est très, très faible; la masse très petite; quand à la Gravité on ne peut agir.... peut-être un jour sur la Lune !
Mais cela donne pratiquement une bonne idée au Pratiquant, et de manière simple.... donc à ne pas négliger. D'ailleurs j'ai connu un Couvreur Ardoisier pratiquer ainsi sur Tourelles et Abside biaisé.
Cordialement au 64.
JPA33 +1 D'ailleurs j'ai connu un Couvreur Ardoisier pratiquer ainsi sur Tourelles et Abside biaisé. Le principe est bien connu et très pratique pour aligner des coupes notamment !
J'ai pas tout lu, mais on sens le charpentier dans les appellations ;)
J'aime ces débats constructifs !! Cela m'aide bien à essayer de trouver un juste milieu .
Je pense que quand nous passerons aux applications avec bois proprement dites , toute cette petite théorie et pratique sur papier aura crée des automatismes , car le langage ne changera plus ,et il n'y a pas d'autres choses vocabulaire de plus pour l’arêtier !
Il faudra bien sur y appliquer les termes basiques de travaux en bois (angle de corroyage,tenon ,mortaise ,montant ,traverses , chevrons etc etc !)
'Angles de Corroyages'.... suite aux Exemples donnés sous formes des Surfaces 'aux Lattis' développables, plus ou moins complexes... j'attends de vous lire sur ce thème précis. A mon avis, il va falloir donner une définition Géométrique très, très précise (Arêtiers formes qcq) ...
JPA33 L'angle de corroyage , c'est en fait l'angle dièdre de la pyramide qui sert à corroyer d'un angle précis recherché,les bois placés en arête des ouvrages en fonction de son inclinaison (ex .pied de tabouret en arêtier)
Bien sur il y aura un chapitre complet a ce titre !
sylvainlefrancomtois et des vulgarisations accessibles restent possibles dans le cas ou une demande aurait lieu.
Je ne pense pas que des débutants s'attaquent à ce traité sans considérer la masse de travail à rattraper que cela implique.
Et en géométrie, et en charpente, et en travail du bois.
Tu as posé de solides bases à l'élévation de ta propre pyramide de savoir. Tel l'arêtier, ton lexique est structurel

Oak Evidemment cela s'adresse surtout à ceux qui maîtrise déjà les constructions en géométrie plane ,et qui veulent passer à la vitesse supérieure !
Pour moi, celui qui, simplement, lit ce pas à pas magistral, comme celui sur l’escalier, qui croit qu’il va tout connaître, comprendre, maîtriser ces sujets autant passionnant que complexe, se met une sablière proprement dans l’oeil.
Seul la relecture multiple avec pratique de la langue (vocabulaire) dans le maniement des vues permettra de l’intégrer pour la partie théorique.
Pour ce qui est de l’exercice de la pratique, c’est une autre histoire... comme ici par exemple
et pourtant c'est en forgeant que...................
sylvainlefrancomtois c'est en sciant que Leonard De Vinci.
Oak et avec la prononciation italienne ,ça donne quoi ??? ok je
Ça prend du temps de bien comprendre, et il faudra une vie (disons beaucoup de pratique) pour l’assimiler.
Une question toutefois, Sylvain.
Peux-tu ré-expliquer la division par les cordes ?
Notamment sur ce schéma, je ne comprends pas l'ordre de la construction : qu'est ce qu'on trace en premier ? et ensuite.
en premier, les cordes sur l'arc , puisque elles servent à tracer les divisions du développement en vraie grandeur à plat , vois tu
Comme ici ?
Mais comment trouves tu le centre de l'arc de cercle ?
Simplement parce que ils sont tracés au compas (méthode par trois points) ! Sinon pas besoin de centre , des courbes aléatoires tracées a la cerce ça fonctionne aussi
Terrible ! Merci beaucoup (pour la réponse, ton partage et ta patience).
Haaaa le fameux angle de corroyage !!! merci pour ce pas à pas ,c'est captivant, me remettre dans la descriptive, que du bonheur
Sylvain a donné une bonne définition pour un Arêtier Rectiligne, rencontre de 2 Versants plans.
Qu'en est-il pour un Arêtier cintré en Elévation, rencontre de 2 Versants courbes developpables ?
De même pour un Arêtier à l'Arête Rectiligne, rencontre de 2 Versants non plans, mais réglés Horizontalement en liaison avec 2 autres Arêtiers qcq de même type ?
Il y a aussi la Fleche Torche ?
Etc.
De quoi méditer sur les limites de la définition geometrique exacte de l'Angle de Corroyage !
JPA33 Vaste question... Ces espaces infinis, cela m'effraie...
En ce qui concerne l'arêtier cintré en élévation, rencontre de 2 versants courbes développables, l'angle de corroyage en un point donné de cet arêtier est, à mon sens, le demi-angle des deux vecteurs orthogonaux aux plans tangents à ces deux versants en ce point.
En ce qui concerne l'arêtier à l'arête rectiligne rencontre de 2 versants non plans, j'ai du mal à concevoir que deux surfaces non planes puissent se rencontrer en une droite (rectiligne)... Donc, dans ce cas, je ne sais pas...
AMHA il ne s'agit pas d'une droite mais une courbe dont une projection est une droite. L'angle de corroyage est peut être constant dans ce cas. Par exemple,, les premières pyramides postées tout au début avec le cheminement de la pyramide au cône.
Kentaro
1er Paragraphe, Non. Car la Section Droite, selon la définition de l'A.C., perpendiculaire à la Tangente au point commun de la l'Arrête du dit Arêtier cintré, intersection de vos 2 plans tangents aux Versants courbes, ne donnera pas le vrai Angle Matière (Les 2 branches sont des courbes et non des droites) ?
Pour le 2ème paragraphe, j'avoue que c'est un peu plus 'vicieux' !
Pour mieux l'expliquer, il faudrait faire une Epure locale à un point commun sur l'Arrête Rectiligne de cette Rencontre, type Epures de Bouchet. Pourtant ce problème est connu en Architecture.... mais là j'exagère un peu....
JPA33 SI si, si... mais il faut bien lire... On prend deux surfaces courbes. Leur intersection est une courbe. Prenons un point de cette courbe. Ce point appartient aussi a chacune des deux surfaces courbes. Prenons pour chacune de ces deux surfaces courbes, le PLAN tangent en ce point. Pour chacun de ces 2 plans tangents, on a alors une droite orthogonale passant par ce point. On a alors l'angle entre ces deux droites. Et l'angle de corroyage est la moitié de cet angle.
Fait un dessin pour mieux comprendre... ;)
JPA33 L'angle ne sera pas constant évidement , mais chaque fois différent a chaque division, et en progression ou récession linéairement le long de la courbe développée (débillardé) ! il y auras bien sur un chapitre !
Kentaro si les deux versants ont un profil commun ,l’arête en plan est droite , des que le raccord d’arête est sur deux versants de profil différents ,les arêtes en plan sont à rechercher (voir dernier chapitre)
sylvainlefrancomtois Oui! je dis bien "en UN point donné de la courbe d'intersection".
sylvainlefrancomtois J'essaie de traduire... ;) ;) ;) ... "si les deux surfaces courbes sont symétriques, l'intersection (en plan ?? projection ? sur quoi ? sur un plan perpendiculaire au plan de symétrie ? ) est une droite... " Pas facile de se comprendre... ;)
Au fait, y a t'il une différence entre "versant" et "surface" ? et entre "arête" et "intersection" ?
Kentaro (en plan ?? projection ? sur quoi ? ( sur la vue en plan)
"arête" et "intersection" L’arête représente l'intersection de deux versants .
Surface du versant ,ou face versant c'est parfait !
Kentaro Là j'interviens.
Définition d'un Angle de Corroyage :
"C'est l'Angle Dièdre Maximum que forment 2 Versants Plans, de Pentes qcc par rapport à leurs Horizontales, et qui se coupent selon une Arête Rectiligne".
Maintenant :
L'Angle de Corroyage est donc la Section Droite (Perpendiculairement à l'Arête Rectiligne) du Dièdre.... Les Branches Latérales de cet Angle, à tout Point Commun de l'Arête, sont des demi-droites incluses dans chacun des Versants Plans (Dites Asymptotiques car incluses dans les Surfaces).
Jusqu'à maintenant, Sylvain nous propose plusieurs Types de Combles à Surfaces Latérales Courbes, dont les Génératrices sont des Horizontales //es. Les Lignes de Pentes Courbes (Donc variables) de chaque Versant sont donc Perpendiculaires à toutes les Horizontales.
Si à chaque Point Commun, sur l'Arête Courbe Arêtière, on positionne 2 Plans Tangents aux Surfaces Latérales Courbes, et ayant comme Tangentes Asymptotiques les 2 Horizontales, l'Intersection de ces derniers, est une Droite dite Tangente Ponctuelle à la ligne Arêtière Courbe.
Si l'on applique la Définition de l'Angle de Corroyage, nous devons tracer une Section Droite Perpendiculaire à la Tangente Ponctuelle.... Les Traces du Plan Section Droite seront alors des Branches Courbes et non des demi-Droites !!.... Donc dans ces cas, il n'y a pas d'Angle de Corroyage, selon la Définition !!
Mais en pratique, nous pouvons utiliser à chaque Point Commun de l'Arêtière un autre Angle dit 'Angle Matière Horizontal' de valeur constante tout le long de l'Arêtière..... et dont les Branches sont confondues avec les Tangentes Asymptotiques au niveau du Point Commun.
Alors attention de ne pas tout confondre !
Pour être complet, il existe un Cas, où les Tangentes Asymptotiques des Surfaces Latérales peuvent être Perpendiculaires à chaque Tangente Ponctuelle au Point Commun. Ces Surfaces Latérales sont des Surfaces Développables, donc Réglées. Là, on pourra parler d'Angle de Corroyage, puisque les Branches Latérales seront droites!.... Mais *les Sections Droites induites ainsi ne sont pas des Plans //es !!
Enfin, lorsque les Surfaces Latérales, sont non Planes, dites Réglées Horizontalement, mais non Développables, les Tangentes Asymptotiques Horizontales ne ne seront pas //es en Projection Horizontale.
Mais vous aurez tj, à chaque Point Commun de l'Arêtière, un Angle Matière Horizontal, variable en Valeur et en Position Horizontale tout le long de celle-ci.
Dans le dernier croquis de Sylvain, Arêtier Courbe en Elévation, les Faces Matières Délardées, sont aussi Développables comme leurs Surfaces Développables respectives... Leurs Génératrices sont des Horizontales //es en Projection Horizontales
Il n'y a donc pas d'Angle de Corroyage à proprement parlé.... mais des Angles Matières Horizontaux.... beaucoup plus faciles pour tracer sur les Pièces bois brutes.
Bon j'en reste là.... et j'attends pour vous lire à tous.
J'ai relu, mais pardon s'il reste quelques fautes.
JPA33 Merci pour cette magistrale démonstration académique ,je n'en serais pas capable du tout ! En fait c'est ce qui m'a rebuté à l'époque et refermer rapidement les ouvrages traitant d’arêtier avec ce langage ! (ben oui j'ai bac - 5) Mais menuiserie charpente depuis 40 ans !
Ce que je veux dire ,c'est que l'on perd très rapidement les gens intéressés si l'on utilise ce langage (je l'ai souvent vu chez mes apprentis qui comprenaient plus vite à l'atelier qu'avec leurs profs au cfa et ce genre de lectures ) ,c'est pour cela que je fait une approche par immersion direct pratique comme le faisaient les anciens, dans le cadre simplifié et purement appliqué en quelques coups de compas in situ pas loin de l'atelier .
Mon expérience personnelle ,comme je l'ai indiqué au début du pas à pas ,c'est d'avoir été plongé directement sur une épure réelle chez un charpentier ,qui m'a permis de comprendre complètement le fonctionnement de l’arêtier en quelques heures (cela me paraissait avant insurmontable et frustrant ),et surtout pouvoir décrypter les épures sur planches anciennes (plus besoin de lire tout le contenu ) ! Ensuite c'est du travail personnel de tracer des épures d'exercices en compliquant les tracés (pour s'amuser et donc progresser) et tailler des bois en réel bien sur !.
dans mon texte avec le dessin d’arêtier cintré j'avais oublié ""l'angle de corroyage en progression ou récession linéairement""
J'ajouterais que tout cela est vraiment toujours très enrichissant d'avoir des approches différentes mais amicales de partages sur l'air du bois !
Je suis entièrement d'accord avec votre texte qui me paraît sincère.
Personnellement avec mes Apprentis, selon les nécessités de l'Entreprise, je 'faisais avec mes pas pour'. Disons le système du Coatching. Et je faisais beaucoup de choses avec eux.... puis à eux de faire...
Mais il y a le problème du minimum Théorique pour faire un Ouvrage vendu ! Et là les explications sur chantier, pour montrer le pourquoi et comment en Tracage, c'est un peu court.
Avec un Copain Compagnons Charpentier, une fois par semaine, et bénévolement, dans son Bureau Atelier, nous assurions à nos Apprentis (Charpente-Maconnerie-Coffrage et surtout les Escaliers Bétons complexes), par Epures entre autres, ce manque de Technicité..... tout le monde ne fait pas de hautes études dans nos domaines !.... même si pour moi c'est un plaisir, encore aujourd'hui... c'est peut-être de famille ?
J'apprécie votre courage et votre ténacité pour traiter le Sujet des Combles sous diverses formes géométriques.
Étant en Retraite, j'ai enfin le temps pour étudier Géométriquement par Epures, le Trait et la Stéréotomie toutes sortes de Surfaces non planes, mais appliquées, du point de vue pratique,.... sans formules, calculs, Progiciels plus ou moins sophistiqués.... Comme je dis 'Ca montre, mais ne démontre rien'.... ce qui n'arrange pas les néophytes.
Mais je ne suis pas contre...
A plus.
+1 de toutes façons j'attend de voir les retours des prochains chapitres ,quand ce sera purement appliqué sur des travaux en bois ! Et si ma méthode fonctionne a plus
a plus
JPA33 J'ai relu 10 fois et j'ai vraiment essayé de comprendre... :)
Si je suis bien, la définition de l'angle de corroyage est dans le cas de l'intersection de deux plans. Donc, dans le cas de l'intersection de deux surfaces courbes, on ne parle pas d'angle de corroyage ? c'est bien ça ?
Ceci dit, j'ai quand même l'impression que l'on peut définir quelque chose comme un angle de corroyage (ou dans ce cas, des "angles matière" ??) dans le cas de l'intersection de deux surfaces courbes. Et dans ce cas, j'en reste à ma manière de déterminer cet angle: En un point donné de la courbe d'intersection, c'est l'angle des deux plans tangents en ce point aux deux surfaces courbes.
Ou pour dire les choses autrement, on a une définition de l'angle de corroyage à partir de l'intersection de deux plans. Quand il s'agit de deux surfaces courbes, on va chercher les deux plans tangents à ces deux surfaces, et on a alors un angle qui correspond au concept d'angle de corroyage. Bien sur, cet angle est variable en tout point de la courbe d'intersection.
Par contre, je n'ai pas compris le reste, je ne sais pas ce qu'est une "section droite" qui serait aussi un angle... Je ne sais pas non plus ce que sont les "branches latérales"... et c'est pareil pour la suite. Bref, je ne peux pas comprendre, car je n'ai pas les définitions des termes que tu utilises... :)
Tu manies là avec brio des concepts, c'est fort bien, mais il est difficile, pour les gens qui ne parlent pas ta langue, de comprendre...
Mais je vais m'arrêter là, car on pollue inutilement le discours de Sylvain, qui a sa propre logique de progression pédagogique. Laissons le faire, il sait où il va.
Kentaro "et on a alors un angle qui correspond au concept d'angle de corroyage. Bien sur, cet angle est variable en tout point de la courbe d'intersection."
"Par contre, je n'ai pas compris le reste, je ne sais pas ce qu'est une "section droite" qui serait aussi un angle"
Oui à priori c'est ça ! regarde le dessin ci dessous ,j'ai dessiné les sections et les déformations induites par la progression d'angles suivant la courbe !
je vous fait une petite avant première du hors série ! voila de quoi visualiser un peu ,l'angle de corroyage en progression ou récession linéairement sur la courbe un arêtier cintré !
Le cachet d'aspirine est fourni avec le hors série ou il faut le prévoir à part ?
On en a déjà parlé mais en plus je trouve ça beau une épure...
non c'est comme dans PIF ,le cachet c'est le gadget !
Ce HS m'a l'air d'être bien touffu, j'ai déjà hâte !
Tant que j'y suis, est ce qu'il y aura un chapitre sur la lecture d'épures ?
On apprend à les faire, c'est vraiment bien. Mais quand on tombe sur une épure ancienne, o,n est vite perdu (mais moins qu'avant).
trente six seb hello , En fait c'est comme le pas a pas que je fait ici , il faut décrypter les fondamentaux ! et après quand on comprend le déroulé du tracé d'épure (vue en plan ,élévation rabattement et développement ) on peut commencer à lire des épures un peu plus complexes a chaque fois!
La photo que tu as mis, est connue ,il me semble qu'elle se trouve dans un musée (àTours ou Romaneche Thorins )
C'est une épure de lucarne guitarde ! on y vois la vue en plan , et surtout de la stéréotomie de pièces (c'est le but )
sylvainlefrancomtois Exact, Musée de Romanèche, car Diplôme signé par Guitton.
Au Musée de Tours il peut y avoir une maquette, mais celles-ci tournent souvent entre les Musées de Compagnonnage du Devoir.
Pour voir de visu, de belles Guitardes en place, il faut venir
à Bordeaux...... mais plus simple, voir sur Pinterest.
sylvainlefrancomtois pour le chapitre sur la lecture d'épure complexe, je parlais de de ce pas à pas ;-)
Effectivement c'est une guitarde, c'est le premier lien "sympa" dans google image.
JPA33 : à Châteauroux, il y en a 2 ou 3 de vraiment sympas.
trente six seb "je parlais de de ce pas à pas ;-)" Eh bien je dirais que l'ensemble permettra plus tard à ceux qui s'y intéressent de près ,de pouvoir décrypter plus facilement les épures complexes !
Perso , moi le premier, après avoir appris les rudiments en arêtier , j'ai ensuite évolué plutôt en "lisant" des épures sans trop me préoccuper des textes , car seule la mise en pratique m’intéressait !
Superbe travail! Une petite précision sur les définitions de la ligne de trave/ligne de sol, en charpente elle est la ligne horizontale à l'intersection du dessus du lattis avec la coupe aplomb du bout des chevrons et en tant que tel elle ne représente ni le dessus des arases de mur ,ni le dessus de sablière, ni le sol puisqu'elle dépend de la saillie des chevrons. La nommer ligne de sol me parait une simplification destinée à simplifier le travail dans le cas des maquettes.
Très juste ! d'ailleurs je l'ai expliqué rapidement au dessus (ligne de trave = lattis (dessus des chevrons)!
Ligne de sol ,c'est plutôt en menuiserie ou ébénisterie (là ou repose l'objet à réaliser comme référence (sol, plateau d'établi, )
Ici je n'aborde pas ou peu la charpente ,et j'essaye seulement de faire comprendre le principe de l’arêtier à une majorité de gens passionnés par le travail du bois novice ou non pro
c'est beau comme de la musique! j'adore! si seulement j'avais pu t'avoir en cours!
l'art du trait !!
Ça c'est de l'article !!! Ne te dépêche pas trop pour faire le suivant, on a du boulot, là !!
+1 super Sylvain ! Merci d'occuper mes soirées !!!


Bravo Sylvain.
J'ai apprécier votre dernier travail sur les systèmes Pyramidaux... en Développements, en Pénétrations diverses (Ou Collisions diverses.... qui sont aussi des Pénétrations !).
Employer le terme de "TroncPyramidal" tel quel, dans votre Etude, est correct, .....mais a aussi un caractère plus général, car ici les Arêtiers/Noues convergent toujours vers un Sommet Point Fixe. Dans un système TroncPyramidal qcq, la Convergence des Faces inclinées n'est pas forcément un Sommet Point Fixe, .....ce peut-être aussi une Arête Faitage Rectiligne qcq !!
Je pense que cette précision est utile.... lors de l'exécution de certaines Epures (Surfaces Gauches, sans le vouloir).
Beau travail abordable.
oui pas de soucis , mais plus tard ,pour l'instant laissons digérer !
Salut Sylvain, je viens de tombé la dessus, ca va occupé mes soirées quelques jours!
J'ai une question au sujet de:
"Développement d'une face du dôme de pyramide en courbe :
A/ Sur l’élévation frontale, nous divisons l'emprunt en huit segments réguliers par le compas cheminant de proche en proche . puis par des fuyantes horizontales , nous projetons toutes ces divisions à l'ensemble de l'élévation .Cette dernière opération, nous donne des nouvelles coordonnées nécessaires à la suite du tracé depuis une courbe . "
Comment faire pour diviser régulièrement l'emprunt avec le compas étant donné que nous ne connaissons pas la longueur et qu'on fait un peu ce dessin pour la déterminée?
Merci en tout cas, c'est très instructif!
Il faut faire le Profil du Versant, ou de la face courbe, que vous voulez diviser en segments égaux au compas. Ce Profil est un Plan Perpendiculaire aux Horizontales du Versant. En fait vous voyez le Versant courbe par bout en Vraie Grandeur.... Ensuite, à vous de jouer.
JPA33 +1 si la courbe d’origine est tracée au compas en connaissant les centres !
hello huit segments réguliers par le compas cheminant de proche en proche , et bien tu chemines ton compas écarté sur la courbe à diviser , et tu le réduit ou tu augmentes jusqu'à obtenir huit divisions !
Quand la courbe est aléatoire ou sans foyer au départ , c'est la seule solution
sylvainlefrancomtois Cela s'appelle "La Division d'un Segment par Convergence"..... Classique.
Mais restera quand même une approximation, car vous faites cela pour un écartement donné du compas !.... que par la suite, vous reportez sur une droite dans la Développée du Versant ? Si vous changez par un autre écartement du Compas (Donc un nouveau n x E), vous verrez sur le nouveau report source la Droite, une différence par rapport au précédant report !
Conclusion : Plus la Courbure du Versant est forte, plus il faut réduire l'Écartement du Compas et donc augmenter la valeur entière 'n'.
Faites un essais pour vous en rendre compte.
Du fait que la distance reportée est une corde et non un arc, en augmentant n la différence avec la vérité sera moindre, mais dans l'absolu la distance reportée sera toujours trop courte. D'un autre coté il faut bien trouver une solution.
JPA33 et kaj+1 Complètement , il faut "doser" le nombre de divisions en fonction du rayon supposé des courbes !
Parfois en art du trait , il faut même re diviser plusieurs segments en deux dans des courbes irrégulière pour trouver de la précision supplémentaire !
kaj et sylvainlefrancomtois
Et bien je vous donne une solution pratique.
Q.q.soit la forme de la Courbe Plane en Vr. Gr., dans le Profil Vertical, vous relevez à la Bande de Papier (Contre un support à former par exemple) la Longueur maximale du Développée de l'Emprunt du Versant Courbe en Elévation.... puis vous utiliser la méthode de Division dites "par Dichotomie" !
Les nombres dichotomiques sont 1, 2, 4, 8, 16, 32,..... etc,
Si 'L' est la Longueur relevée en Courbe Plane du Profil avec la Bande à Papier (Ou un Mètre Ruban)..... et que vous vous voulez diviser la Développée 'L' en 7 Segments égaux, par exemple,... vous divisez 'L' par 7, puis multiplier le résultat par 8 (Valeur Dichotomique la plus proche),
Ensuite vous positionnez votre Mètre Ruban sur la Développée de 'L' (Ou sur la Ligne Courbe du Profil d'Emprunt), bien contre le Support (droit ou courbe), à partir d'une Extrémitée,....puis vous repérez l'autre Extrémitée de valeur F = ('L'/7)x8 (Elle peut être sur ou en dehors de la Bande).
Enfin :
-Faire mentalement (F:2) et marquer un trait,
-Faire encore mentalement ((F:2):2) et marquer un trait,
-Dito mentalement (((F:2):2):2 et marquer un trait.
Il y aura donc en-tête déjà 2 Segments trouvés, que l'on peut reporter avec une autre Bande à Papier sur la 2ème partie et la 2ème partie sur la 3ème…. avec un dépassement de 1 Segement, c'est normal dans mon exemple, il ne faut garder que les 7 Segments.
Cette méthode (Peu connue) est souvent employée sur les Chantiers, en Epures, en Dessin sur du linéaire ou en courbe,....etc.
Je vous recommande de l'essayer avec Mètre-Ruban, crayon, une simple calculette si le calcul mental vous perturbe.
L'avantage de cette méthode, est rapidité, relativement simple, et, si une erreur est tj possible, elle ne sera pas cumulable en cours de traçage!…. donc facilement repérable visuellement et corrigeable après coup.
A vos essais....
Okay je vois l'idée.
Merci pour vos réponses, je continue alors la leçon! ^^
JPA33 Interessant, mais moins rapide que le compas ,il faut trois minutes à un ouvrier expérimenté pour tracer des divisions au compas ! Et pour la prise de mesure ou le tracé d'une courbe par points ,une cerce ou un mètre pliant sur la tranche et quelques plots ou un collègue suffisent !
Et atelier rapidité et technique sont de mise , bien souvent la théorie (incontournable en apprentissage) est abandonnée au profit du savoir faire pratique !
Si j'ai bien compris ça donne ça
kaj Belle démo appliquée encore une fois signée Jacky !
sylvainlefrancomtois
Moins rapide !!
Essayer d'abord de bien maîtriser le principe.... et après en Situations réelles sur Chantiers ou Ateliers, q.q. soit nos Métiers, vous verrez pour la rapidité, la justesse et surtout le non cumul des erreurs qui peuvent être tj possibles.... mais corrigeables immédiatement sans tout refaire.
Pas très connue des Jeunes, mais très pratiquée par les Anciens.
kaj Oui, et essayez d'appliquer sur la Bande ou Cerces déployées, la méthode par Dichotomie (Divisions successives par 2, après avoir déterminé 'L' comme décrit plus haut.
Plus précise, car vous travaillez sur un Linéaire (Segments droits), ou sur Courbe continue (Longueurs d'Arcs).
Segments droits = Longueurs d'Arcs !!
kaj Apres un léger retard de ma part, bravo.... et je confirme votre essai.... vous avez tout compris.
Je souhaite que d'autres praticiens essayent, c'est un très 'bon outil' à adopter dans de nombreuses circonstances chantier.
La pratique continue, diminue le temps d'exécution en traçage.... et surtout les 'erreurs dites cumulables'.
J’apprécie particulièrement ce dernier chapitre. Il rapproche le trait du Traçage j'ai eu la chance au cours de ma carrière de côtoyer des fumistes férus de cette discipline. J'ai beaucoup appris à leur contact. Il est aisé de comprendre que de tracé le développé de pénétration d'un cône à sommet inaccessible dans un cône a sommet déporté présente quelques difficultés; quand à sa réalisation dans de la tôle de 12mm elle n'est pas plus simple.
Encore merci Sylvain.
La tôlerie de façon générale m'a beaucoup apporté (lecture) zinguerie, chaudronnerie , leurs tracés chez les compagnons m'avaient épatés ,car il faisaient leurs épures d'exercices sur papier qu'ils découpaient ensuite pour voir le résultat !! D’où la manière que j'explique ici de faire découvrir l’arêtier ,tu verras dans le prochain chapitre la subtilité de commencer par des développements de surfaces ,ça devrais plaire !
sylvainlefrancomtois
La Charpente ce n'est pas uniquement du Surfacique, mais une partie nécessaire..... contrairement à un Couvreur, qui lui travaille sur du Surfacique.
JPA33 Oui bien sur !! les deux sont complémentaires en fait , par exemple nous donnions l'épure de charpente toiture ronde au couvreur pour qu'ils fassent leurs rangs de coupes !
conversation du plus intéressante,la tôlerie est un métier passionnant et beaucoup plus "théorique" que ce que l'on croie.
ckarriere Complètement !!
Je suis plus qu'admiratif... C'est tellement bien expliqué pour quelque-chose d'aussi complexe.
Pas facile de transmettre cette connaissance, sur le papier, sans pouvoir s'expliquer face à face, montrer directement. Et pourtant tu y arrives ! Bravo.
Déjà le pas à pas sur la charpente était merveilleux, et m'avait donné envie d'approfondir le sujet du trait.
Merci !
merci, j’espère que la suite plaira aussi !
Sans aucun doute.
Merci Sylvain de nous partager cette connaissance , qui nous donne l'aire que c'est abordable ! je serais heureux d'acheter votre livre ! ;) y avez vous pensé ? car je n'arrive pas à trouver un bon livre sur le sujet qui explique d'une façon simple et compréhensible aux débutant comme moi dans ce domaine du tracé ! .
Pas encore eu le temps de me plonger dedans mais regardez Cours de trait, premier carnet de Patrick Macaire et Maurice Pommier. Ça pourrait correspondre à ce que vous décrivez.
(J'essaierai de faire les revues sur l'adb quand j'aurai fini ma pile de bouquins).
Bonjour Sylvain , sur l'Agrandissement n°1 du sujet "Tracé et exécution d'une pyramide régulière en panneau de 22 mm", je ne vois pas de différence de résultat entre la méthode correcte et celle incorrecte :
-pour l'incorrecte, on part du point de coupe, on le pivote d'~120°
-pour la correcte, on part du point de coupe, on le projette sur l'emprunt, puis on le pivote d'~120°, puis on le "déprojette" depuis l'emprunt
Merci de ton éclairement. Merci pour ce partage de grande qualité.
-pour l'incorrecte, on part du point de coupe, on le pivote d'~120° , c'est simple il te déporte sur la ligne de sol le point a rabattre, et donnera une coupe fausse ! (le point d’interrogation ? explique bien le mauvais principe ) vois tu ??
En résumé tout doit être projeté depuis l'emprunt sur lequel on projette les points secondaires !
Si j'ai bien compris, en menuiserie nous recherchons l'angle de corroyage ( ça ne me pose pas de problème ), En charpente dans le cas d'un chevron de noue, la section du bois est rectangulaire, mais il faut trouver le pas au sol , donc c'est le même angle mais dans l'autre sens. Quand j'ai fait la maquette j'ai bien galéré pour trouver, mais là ça s'éclaire! Dis moi quand même si " j'ai bon"
Oui c'est ça Jacky , en charpente nous recherchons les angles des délardements , ce qui correspond vu par bout à un angle de corroyage, mais chaque fois sur des bois face aplombs !
sylvainlefrancomtois merci Sylvain, quand on a l'habitude de regarder d'un sens il est difficile d'inverser le raisonnement et pourtant c'est le même.
sylvainlefrancomtois l'Angle de Corroyage concerne les 2 faces planes de par et d'autre de l'Arête droite du Dièdre..... angle concave ou convexe,... Flans lateraux Aplombs ou pas,... sous-face plane, 2 faces planes formant angle concave ou convexe (Bien sur contenu dans un plan perpendiculaire à l'Arete dite principale.
Pour les Pièces dont une Face est au Lattis et l'autre non au Lattis, on rentre dans les notions de Dévers de Pas qu'il faudrait détailler à part !
L'Angle de Corroyage est ici un Angle Matière dans les EXEMPLES EVOQUES ICI, Dans le cas plus général l'Angle Principal Matière sera tj Horizontal (Ou les....) et dont les 2 branches seront droites et incluses dans les Surfaces Adjacentes (Delardements).
En tous cas validation de votre dernier envoi... j'apprécie.
JPA33 merci !
La différence essentielle entre charpente et menuiserie et qu'en charpente on travaille généralement avec des bois qui ont leurs faces d'aplomb alors qu'en menuiserie le problème est d'avoir des chants d'équerre aux faces pour pouvoir y pousser des moulures et faire des assemblages et c'est là que les choses se compliquent quand on aborde la courbe!
Paco64 +1
sylvainlefrancomtois C'est un travail absolument impressionnant que tu fais la! Bravo!!
Merci du retour , l'essentiel c'est que ce soit compréhensible pour tous ! à priori c'est le cas !
Bonjour, sur le dernier schéma je me pose une question concernant une des vues de la pyramide triangulaire. Sur la vue en bas, à droite, on voit que tu as tracé la hauteur du triangle depuis l’arête en vraie grandeur. Ensuite tu rabat celle-ci sur la ligne de sol puis tu projette ce point sur la vue de dessus. jusque là, tout va bien. Mais c'est le choix des autres intersections (pour former le triangle dont on pourra mesurer l'angle) que je ne suis plus : tu obtiens un quadrilatère, et non un triangle comme sur les autres vues, et je ne vois pas comment tu as fait ?
Tres juste !! comme l'angle en plan de la pyramide à cet endroit est obtu (+ de 90°) ,c'est l'alignement de l'angle perpendiculairement à l’arête qui se retrouve donc à 90° pour tracer l'angle de corroyage !
Je viens de matérialiser sur le dessin par le symbole d'angle droit en rouge .
Une bible ! Merci !
comme vous dites, la géométrie descriptive est la manière pratique de visualiser un tas de calculs complexes. Vive Monge et la descriptive, qui m'ont bien aidé en coupes et jonctions des tuyauteries et travaux en chaudières. Je vois que c'est pareil en menuiserie, bien que les thermes en français m'échappent un peu. Bravo pour vos explications, qui sait si faire un peu plus de dessins et moins de théorie serait plus "compréhensible"?
j'attend la suite :)
merci
Je viens de lire des fragments de ton magnifique article...je dois dire que je suis loin de tout comprendre .
Quel travail !
Je vais reprendre ce pas à pas depuis le début.
Merci , j'essaye de faire pour que tout le monde comprenne a son rythme !
sylvainlefrancomtois j ai trouvé ça dans mes reliques ça peut intéresser certains
Palissandre A c'est du Roubo !! Ici c'est pour apprendre à dessiner (pas épure) , perspectives avec points de fuites ,très utile et ancêtre de sketchup .
.
C'est ce que l'on appelle la Perspective Conique.... très utile pour du/des rendu(s) visuel(s).... Toutefois ce n'est pas de
la Perpective Stéréo réelle(2 Foyers).
Plus proche dans la pratique de certains Métiers, la Perspective Axonométrique (Fuyantes //es, Tableau Frontal en Vr. Gr. et Plan de Base Hor. Incliné en Vr. Gr.)... où dans celle-ci on peut avoir des Longueurs en Vraie Grandeur.... mais, attention, pas tous les Angles !
Cordialement.
mes cavalieres et avec points de fuite du travail perso qui n'etait pas au programé dans mes cours de C.A.P. "dessin bâtiment" de 1961
Une autre fiche memoire " mise au propre " en 1971 et une realisation bois une autre epoque ...
les photos du message precedent
sanglier hello ici une question qui peut t’intéresser ! lairdubois.fr/..._comment_134075
si tu pouvais nous faire l'épure détaillée d'un Buenos aires sur plan rectangle ce serait super ! merci
sylvainlefrancomtois ily a eu une realisation sur ce site il y a quelque temps je n'ai plus l'epure ... par mon niveau C.A.P. DE 1960 et mes souvenirs d'epoque c'est toulours vue nn pla le chevron d'emprunt pour hers et les reports de demaigrissements dans mes epures souvent un peu de trigo pour de precisions tracés j'ai arreté ces etudes car c'est du pas solide : ça vrille ... cette table à la mode est peu stable beaucoup trop de porte a faux et on met tougour un entrait ou tirant entre des pieds d'arba ne pas copier sans relechir à la solidité surtout pour vendre c'est une responssablité
sylvainlefrancomtois Je suis ta publication avec intérêt car elle m'ouvre de nouveaux horizons... J'en suis actuellement aux exercices de tracés d'épures. Je vous mets celle de la pyramide irréguliére (sous réserve d erreurs..) et je vais continuer avec des épures plus compliquées. J'avoue que ces exercices éclairent bien ma lanterne.
Une question pour la réalisation : on doit normalement refaire l'épure à l'échelle 1 (ce qui n'est pas si évident en réel..), et on présente les pièces brutes sur l'épure pour relever dimensions et angles... j'ai compris mais je ne suis pas encore passé à la pratique..
Peux t-on faire l'économie de l'épure échelle 1 en ayant toutes les infos données par le logiciel (pour ma part Qcad ou SKP) angles, dimensions; il me semble que oui.
Ton avis?
merci de ton travail
Hello merci que mon travail te plaise !
Je vais répondre rapidement , attend ce soir je devrais avoir fini le premier chapitre des exercices pratiques , tu auras déjà des réponses !
Alors oui c'est possible de travailler par calcul , mais le tracé des bois sera très long et compliqué en terme de visualisation (j'ai appris aussi à calculer, mais je ne m'en suis jamais servi) . Une épure échelle 1 reste le meilleur moyen de tracer et exécuter précisément en limitant les erreurs et de tout contrôler par superposition des bois dessus !
Ce soir donc tu auras des réponses , et peut être d'autres questions ? et bravo pour ton épure d'étude !
+1 !
Avant de faire une épure réelle et présenter les bois dessus, j ai voulu le faire virtuellement dans scketchup (comme le présente sylvainlefrancomtois dans son exposé) pas du tout facile en fait de présenter virtuellement la pièce et la tracer...j'ai fini par couper les pièces (virtuellement) en utilisant la fonction "découper" (dans la version pro demo).
Bravo à sylvain pour toutes ces épures commentées qui nous éclairent bien.
Merci. Voilà qui va être utile!
de rien ,fait nous partager l'utilité pour toi !
Sylvain ton pas à pas est un régal!!!
Il mériterait d'être edité.
Bravo
Jean-Paul
merci , peut être un jour ??
Coucou Sylvain, Je suis un peu éloigné de tes écrits pour l'instant, mais quand j’aurai un peu plus de temps je vais suivre tout ça. Merci d'avoir référencé ma modeste contribution en la matière.
pas de soucis je met à mesure que je rempli !
je met à mesure que je rempli !
Joli cadeau de Noël..... il va falloir trouver du temps pour certains.... A vos Epures à tous et bonnes fêtes.
Génial tout ça de voir les volumes, les différentes étapes de traçage et de taille des blocs! Je serai toujours admiratif devant tant de travail.
Un énorme merci!! Ce cours est juste parfait!
Hello sylvainlefrancomtois
Ça a déjà été évoqué mais je ne sais plus où et malgré les recherches je ne retrouve pas.
Tu conseilles de commencer par quoi :
Merci
Les 2
En fait pour appréhender le trait , l’arêtier droit et généralement le premier ! puis l’arêtier cintré, et enfin le cylindre (débillardé) , enfin viens le cintré en plan et élévation (ou croche pour les charpentiers)
le pas à pas sur l’arêtier je l'ai fait pour un apprentissage à son rythme , chose que j'aurais aimé avoir en son temps !!
Apres , généralement on connait le principe général et on peux petit à petit explorer ce que l'on veux !
Hors Série du Bouvet c'est plutôt une présentation d'ensemble pour la transmission que cela existe (beaucoup de gens ignorent ce qu'est l'art du trait (même des pros)
pour commencer familiariser avec le trait ici c'est bien
En fait tu me conseilles de travailler plutôt par "thème" que par support ?
L’exercice de la pyramide en arêtier droit sur plan carré (dans le HS du Bouvet)me parait plus simple que les exercices de kaj.
Tu fais en fonction de ta sensibilité et de tes capacités actuelles , dans ce pas à pas tu as tout pour progresser à mesure, c'est son but !
ex : Fais une pyramide en panneau 22 mm ou autre massif pour te familiariser avec le tracé et les angles a trouver (une tirelire par exemple) , puis tu augmentes les difficultés , il n'y a pas de limites !
Héhé, intéressant. Je suis aussi en train de travailler sur l'arêtier...
Mais j'ai de l'avance sur toi trente six seb, j'ai déjà réalisé la trémie :p
Je réfléchis à la suite. Sûrement une pyramide avec quelques particularités.
En tracé j'en ai sûrement fait un peu plus que toi.
Mais pour l'instant, je n'ai pas taillé un bout de bois.
Hier j'ai tracé une auge avec les coupes d'onglet. Tu veux l'exercice ?
Merci sylvainlefrancomtois
En fait le hors série est plus large que l'arrêtier. Je reprends au début et mixerai en avançant.
Commencer par déterminer par Epure les Angles de coupes d'un Tétraèdre quelconque dont les faces ont même épaisseur. = 6 problèmes différents à traiter.
trente six seb oui je veux bien, merci !
JPA33 je note, merci.
JPA33 je crois que je vais d'abord commencer par une pyramide régulière.
Et plutôt sur un vrai projet. J'ai une petit idée en tête.
trente six seb celui ci est sympas comme inspiration !
paruvendu.fr/a...1305A1KBMAME000
Je vais faire plus petit
sylvainlefrancomtois Oh oui..... Par exemple, couper une Pyramide à Base Triangulaire quelconque, à mi-hauteur environ, par un Plan incliné quelconque.... et trouver par Epure, TOUS LES Angles nécessaires à TOUTES les Arêtes Dièdres du Tronc Pyramidal (9 u).
Après, si vous en avez pas assez, faire la même chose.... mais en prenant les 3 Arrêtes Inclinées, issues de la Base, NON CONVERGENTES. Attention il va falloir réfléchir....
JPA33 merci pour les idées :)
sylvainlefrancomtois J'aime beaucoup ce meuble ! Je le remets ci dessous pour mémoire.
Notez les coulisses des tiroirs, astucieuses.
Pour l'instant j'en suis là...
Je n'ai pas terminé le même tétraèdre coupé par un plan.
hello , faites des pas à pas de vos progressions dans le trait , ce serait très intéressant , faire la tambouille a plusieurs c'est sympas non ?? !
why not, je suis à l'avant dernier exercice des 20 leçons !
J'anticipe pour la suite.
dneis : je vais faire une question et poster le sujet
ah moi je ne me sens pas encore assez compétent.
Je ne fais que débuter et je me contente de refaire des figures des bouquins que j'ai dans ma bibliothèque (le Lucien Chanson en l'occurrence pour l'instant, que j'aime bien).
J'aimerais bien trouver un moyen d'imprimer les pages de l'AdB de manière propre. Il faudrait créer un bouton imprimer qui génère un pdf avec une mise en page correcte. Mais c'est du boulot, et je pense que je ne saurais pas développer cette fonctionnalité.
Le gros du boulot est la gestion des images... Car certaines images ont besoin d'être grandes pour être lisibles, d'autres sont moins nécessaires... La solution technique me paraît épineuse
C'est vrai qu'il a l'air bien ce bouquin aussi.
Oui pour les images, ça a toujours été le souci des forums ou autres sites communautaires. Il n'y a pas de solution parfaite. Au moins ici, les images sont pérennes car sauvegardées sur le serveur. Mais elles sont systématiquement comprimées.
L'une des solutions et de publier des plans qui permettent de joindre des fichiers.
Ça serait sûrement bien aussi de pouvoir joindre des fichiers dans la messagerie mais le serveur risque de ne pas aimer ^^. Sauf à prévoir une date de limite de conservation des PJ par exemple.
sylvainlefrancomtois je viens de commencer la lecture de ton pas à pas en détail. C'est admirablement bien expliqué, merci. Et je sens que cela va répondre à beaucoup de mes questions actuelles sur le sujet.
Juste deux petites questions:
sylvainlefrancomtois te répondra mieux que moi, mais tu peux déjà jeter un coup d’œil ici lairdubois.fr/...entaires/126134
Est ce que l'emprunt est aussi appelé "ligne de plus grande pente" je sais pas , j'ai jamais entendu dans mon apprentissage !
dneis
Effectivement de ce que j'ai appris l'emprunt est la plus grande pente. A savoir le chevron perpendiculaire à la sablière en charpente.
Ok, c'est donc la même chose. Chanson, dans son livre, utilise le terme LDPGP, définie comme (Pl. 22, fig. 16):
dneis ben... vous avez la très bonne réponse.
En fait c'est aussi la définition d'une Surface Plane de Pente maximale..... La Sablière pouvant être non Horizontale !
Emprunt = chevron d'emprunt ici ? Pour moi emprunt signifie un peu comme virtuel en optique. Si on a une sablière de pente, on a aussi une sablière d'emprunt et c'est à cette sablière virtuelle (qui est la trace horizontale) que le chevron d'emprunt sera perpendiculaire.
dneis Ok ! c'est logique évidemment ! donc l'apothème !
En pratique j'ai appris comme cela /
L'emprunt ou chevron d'emprunt :
il représente l’apothème d'un pyramidal ou d'un conique,donc le profil frontal de l’arêtier et de la face versant encore inconnus en vraies grandeurs ! Il sert aussi à tracer des épaisseurs de bois à œuvrer ou à reporter (nous le verrons plus tard).
Chez les charpentiers , il se nomme le chevron d'emprunt ,chez les autres professions généralement seulement l'emprunt .
Glorfindelrb une Sablière de Pente n'est pas Horizontale dans un Versant incliné !
Par contre un Chevron d'Emprunt (Ou Ligne de Plus Grande Pente du Versant est Peroendiculaire à toutes Horizontales du dit Versant.
Cette sabliére « virtuelle » est appellé sabliére de déguauchissement.
Boisbarbu ???? La Sablière n'est pas "virtuelle".... mais rampante sur son mur porteur biais par exemple.
JPA33, Boisbarbu ne parle pas de la sablière de pente mais de la droite formée par le plan et l'horizontale que j'appelais sablière d'emprunt (je pense avoir lu ça chez Michel Verdon). On trouve égout de pente et égout de dégauchissement (pas le même ligne mais même idée) dans l'Emery.
C’est ça!
Boisbarbu Merci des précisions, pour mieux vous comprendre.
Par contre à me préciser ce que vous entendez par..... Sablière de dégauchissement ?....
Une Sablière, en temps que Pièce de Bois de Charpente, est Horizontale ou de Pente pour recevoir les Pieds de Chevrons, ou de supporter les Chevrons saillants vers les Egouts Horx ou de Pentes.... ces Chevrons étant toujours perpendiculaires à une Horizontale du Versant.
JPA33 , la sabliere de dégauchissement n’est pas une piéce de charpente. C’est une ligne virtuelle, que l’on trace pour la recherche de coupes. Elle est positioné au niveau de la ligne de trave (altitude 0 d’un tracé de charpente).
Boisbarbu Ok.... merci pour votre précision, je comprends mieux le qualificatif 'dégauchissement'.
A moi de poser une question... qu’est-ce que l’égout Horx? = De niveau?
Merci
Boisbarbu Dans le Plan Lattis (Dessus Chevron) du Versant, c'est la Ligne la plus basse (d'Egout), qui peut-être Horizontale ou non.
J'ai pas fait de dessin , mais voilà un bon lien !!
apprendrelacha...e-de-pente.html
Je connais.
Pas mal et bonne pédagogie....
En ce qui concerne les Pieds en Dévers de Pas, tout au moins au début, je me pose la question, pour les Apprenants, s'il n'était pas utile "d'extruder" ce problème unique sur un Pied.... de l'Épure générale, pour montrer toute la Géométrie Spaciale par l'Usage du Trait..... aux instruments classiques.....
Beau travail quand même.
Bonjour Sylvain et merci pour tout ce savoir que tu partage et qui m'aide a regretter un peu moins d'avoir fait de l'informatique et pas les compagnons quand j'en ai eu l'occasion
J'ai failli poser une question stupide et puis j'ai relu et j'ai compris ! Ta méthode pédagogique est vraiment très bien pour quelqu'un comme moi qui n'y connais rien !!
Ta méthode pédagogique est vraiment très bien pour quelqu'un comme moi qui n'y connais rien !! 
Encore merci.
Petite question quand même tiens (y'a pas de raison que je passe une occasion de passer pour un ane ), le développement a la herse, n'est-ce pas le même principe qui est utilisé dans ton traité sur les escaliers pour le balancement ? (une des méthodes en tout cas).
), le développement a la herse, n'est-ce pas le même principe qui est utilisé dans ton traité sur les escaliers pour le balancement ? (une des méthodes en tout cas).
pour le principe oui, sauf que dans l’arêtier tu as aussi les parties arrières qui apparaissent après avoir rabattu à plat , vois tu ? nous ne sommes plus dans de l'orthogonal, mais dans du géométral (profondeur en plus) !
Oui je comprends c'est plus clair
c'est plus clair 
Impressionnant et très intéressant papa comme tjs



tu as de la chance, bientôt des cours privés ! mais avant continue sur ta lancée et apprend bien les fondamentaux nécessaires !

Bien bien bien...
En plus de l'arêtier, ça échauffe pas mal sur sketchup. Les queues d'aronde m'ont vraiment donné du fil à retordre, je crois avoir recommencé le tracé 5 ou 6 fois. J'ai eu du mal à bien comprendre et interpréter les lignes de niveau. Mais c'est rentré !
hello , as tu tracé l'épure ?
-Dito, montres-nous ton Epure !
-Et dis-nous, au vu de la photo, comment tu as procédé au montage des 4 pièces de ton Ouvrage !
Dans ce cas précis, donnes-nous la nature de la Direction d'Assemblage de chacun des Assemblages Dièdres (Tes Arêtiers), au droit de chaque Plan de Joint !
-Comme tu n'as pas employé la méthode classique, possible ici puisque il y a 2 plans Vert. de Symétries, peux-tu nous expliquer :
.Les différences entre ces 2 méthodes.
.Les conséquences visuelles alors des Assemblages en Arêtiers !
.La nature alors, des Directions d'Assemblages dans cas precis !
C'est bien d'avoir commencé par des 'Doubles Queues Droites'..... et comme tu nous a présenté en premier, une application de la Méthode Générale d'Assemblage 2 x 2 Eléments Primatiques inclinés sur un Cas particulier..... je pense que tu peux maintenant, si tu as bien compris le mécanisme, faire la même chose, en visuel, avec de vraies Queues d'Arondes et en Inter-Queues aussi !
Bon challenge.... en Epure d'abord.
Bonjour sylvainlefrancomtois, voici l'épure, j'ai caché les guides pour ne pas surcharger le dessin et séparé les images pour avoir une vue plus en détail.
Bonjour JPA33 ,
vincentdoreillac hello c'est bien tracé ! Un conseil , dans sketchup, tu vas dans affichage , puis styles d’arêtes , puis tu ne laisses coché que arêtes !
Tu n'auras que des trais fins !
sylvainlefrancomtois merci beaucoup ! Deux fois !
dodo336Z
"Épure présente dans le commentaire précédent"
-Je ne suis pas contre de Sketchup, mais j'aurais aimé une vrai Epure avec ses L.R. !!
"C'est une très bonne question, j'avoue ne pas avoir fait attention aux éventuelles collisions lors de l'assemblage de l'ensemble. Je vais m'y pencher et te donner une réponse car il est vrai que c'est un point essentiel, peu importe la réalisation"
-Eh oui !! Ton Ouvrage en Plan est de forme Rectangulaire et non Carré.
Le/les problèmes sont aux montages des Eléments (4+1) et selon le/les Directions d'Assemblages !!!.... Q. q. soit le Type de Q.A.
"La méthode classique ? Je ne vois pas de quoi tu parles. J'ai peu-être loupé un passage du pas à pas qui parle de différentes méthodes... Si non, je n'ai pas ces connaissances"
-La Méthode classique : La D.Ass. de 2 Eléments formant un Angle Dièdre qqc, est Perpendiculaire au Plan Bissecteur de cet Angle Dièdre.
Votre Ouvrage en comprend 4 à assembler !.... 2 x 2 + 2 1/2 Ouvrage. Le Fond étant Hor. Les D. Ass. aussi.
Là, vous allez découvrir le Problème ?... pour achever votre Ouvrage.
-La Méthode générale : Les D.Ass. de l'ENSEMBLE des 4 Éléments inclinés doivent être Perpendiculaires à chacun des 4 Parements ! Il y aura dont une position Départ udentique pour chacune des 4 Éléments de même Epaisseur !
En interne, et en même temps pour les 4 Eléments, les D. ASS. seront Hors et par Imbrications, Perpendiculaires aux Plans bissecteurs (Si les Epaisseurs des Eléments sont égales).
En fait, si vous aurez décidé de faire le Fond Hor. de votre Ouvrage dito par Q.A.... c'est la seule Solution possible !
"Merci, mais tu me poses une colle... Ce ne sont pas de vraies queues d'aronde ?"
-En fait d'après la photo initiale, je pensai que vous avez fait que des Q. dites Droites ! Peut importe car pour moi, et Géométriquement, la définition du terme Q.A., vu à
chaque Parement des Eléments, peut-être Trapézoïdale symétrique ou pas, Rectangulaire, Carré..... Mais pour simplifier ici, les Faces Internes des 'Q.A.' doivent être des Plans dits Glissants en cours de montage/démontage et des Plans Buttés en fin de montage.
Un point important... la D.Ass. par Imbrication, est ici une Hor. Rectiligne.... mais qui se déplace parallèlement à elle-même lors du Montage et Démontage !!!
J'espère avoir été clair, pour te montrer/voir la difference des 2 Méthodes ?
Sur ceux, c'est tout l'intérêt de faire, dans ton cas, même partiellement, une vrai Epure aux instruments de dessins.
Bon courage et perseverence !
JPA33 bonjour !
Voici l'épure papier, la toute première qui plus est. C'est assez long à tracer, il y a eu pas mal de retouches, de traits inutiles et des erreurs d'alignement. C'est cependant très formateur quant à la méthodologie et l'ordre des tracés. Merci de m'avoir incité à la tracer.
Pour l'assemblage, les Q.A. sont symétriques et leur direction d'assemblage se fait sur une ligne horizontale qui va d'un grand côté à l'autre. On assemble d'abord une face avec ses deux petit côtés, on insère le fond et on referme le tout avec la seconde face.
Je viens de comprendre la différence entre les deux méthodes maintenant que j'ai éclairci celle qui est présentée.
L'épure n'est pas complète, il manque encore le tracé de toutes les rainures mais il devient compliqué de s'y retrouver. La prochaine fois elle sera échelle 1:1 avec une création à la clef, je l'espère.
vincentdoreillac belle épure !
sylvainlefrancomtois merci beaucoup ! Prochain investissement, les crayons de couleur
oulala mais quelle quantité de travail pour écrire ce pas à pas !!! décidément tu donnes beaucoup de ta personne pour cette communauté :) un grand grand merci !
c'est un devoir et un plaisir pour moi !
Salut sylvainlefrancomtois . )
)
Dis, dans la rubrique "Exercices de tracés et développements pratiques pyramidaux irréguliers" Dans le petit H), ou pas loin, tu développes 2 vues perpendiculaires aux arêtes.
Dis moi si je me trompe, ou si j'ai mal compris mais j'ai l'impression qu'avec cette technique (et non pas celles des emprunts) il n'y a besoin de projeter qu'une seule vu car vu dès lors qu'on a projeté la première vrai grandeur sur l'emprunt, les arêtes obtenus nous permettent d'obtenir chaque sommet en reportant celles ci sur les emprunt des faces d'a coté nan? (j'ai pris le mal de mer en expliquant ce que je voulais dire...
je suis en train de finir un article, après j'irai voir !
j'irai voir !
sylvainlefrancomtois Chouette! Ça m’empêche pas d'avancer le reste!
L'Ecorce du Sycomore sur le Buenos aires pour mettre l'eau a la bouche !
sylvainlefrancomtois euh... Je fais les autres exercices d'abord!
euh... Je fais les autres exercices d'abord! 

Le but secret de la démarche est là
L'Ecorce du Sycomore Oh..... les Ambitions sont Hautes.... Bon courage dans l'Art du Trait..... et la manipulation des divers Plans !!!!
Et voilà, une question il y a 22h, et sylvainlefrancomtois nous sort un article de XXX pages (toute ressemblance avec le X du pied Buenos Aires est un pur hasard) en guise de réponse , rien mais alors rien ne l’arrêtera





 ,
, 


sylvainlefrancomtois tu écris plus vite qu’un ciseau fait des copeaux, et la maîtrise de SU, bah moi je suis largué , encore quelques heures de régale pour nous
en fait cela fait au moins trois semaines que je cogite et dessine !
merci du compliment quand même !
Encore un super article, merci Sylvain.
Super article sur le Buenos Aires, ça avait l'air si simple sans rien savoir du sujet, finalement c'est pas simple...
Beacoup de livres n'ont pas la même qualité pédagogique et illustrative !
merci , en fait j'essaye d'écrire ce que j'aurais aimé trouver à mon époque !
Superbe! Merci (encore) pour ce pas à pas monumental!
Encore du super boulot Sylvain


Quel plaisir
Magistral ! Un travail pédagogique impressionnant et limpide ! Merci pour ta générosité !
Bonjour, je suis tombé sur ce pas à pas via le forum copain de copeaux, et un grand MERCI pour le travail accompli ! Je n'en suis qu'au 4 ème chapitre, mais c'est super bien expliqué !
merci
Bonjour mon très cher sylvainlefrancomtois
Je me plonge enfin dans ton pas à pas, très instructif pour moi. Merci !
Une question (probablement d'autres à venir... :) ) : y a-t-il une raison plus qu'une autre pour laquelle nous divisons l'emprunt en 8 segments et pas plus ou moins ? Question annexe mais liée : comment "choisit-on" ce nombre "8" ?
Merci !
merci de l’intérêt pour mon travail !
Alors en 8 car c'est très facile et précis de diviser par les bissectrices au compas ! Parfois on fait au rapporteur en 6 divisions, mais sur une épure de charpente, je te dit pas la taille du rapporteur , alors que le compas c'est du gâteau !
Dans des tracés simples, aretier de charpente regulier, on peut aussi ne diviser qu'avec des lignes de niveaux la hauteur .
8 divisions c'est assez précis pour des courbes en Doucine par exemple , et cela allège le dessin qui comportera déjà bien des traits !
Évidement, dans l'absolu, plus il y a de points plus c'est précis !
Merci beaucoup, c'est très clair :) !
Merci beaucoup sylvainlefrancomtois pour cette somme non pas théologique, mais charpentesque!
Merci d'avoir pris le temps de partager tout ça, de l'écrire, le mettre en forme.
Je n'ai pas tout lu, loin s'en faut, peut être as tu déjà répondu à la question, as tu un livre, un PDF que tu aurais édité, que l'on puisse acheter ?
J'ai fait cela, mais c'est plus pour faire découvrir l'art du trait en général !
Intéressant, merci !
Bonjour
Cet ouvrage est-il un bon point d'entrée dans la compréhension de l'épure ?
Je cherche un ouvrage d'initiation
Merci
Merci beaucoup à toi sylvainlefrancomtois !
( Pas mal pour un "apprenti" ébéniste non ?)
avec du retard !
Remarquable travail, c’est spectaculaire le savoir mis à disposition de ta part, il y a du talent en Franche Comte !!!
et ailleurs ! merci
J'aimerais trouver ne formation qui me permettent de comprendre puis réaliser les épures.
J'ai cherché mais pas trouvé ....
Je vais passer un peu de temps sur votre pas à pas mais j'avoue que c'est pas simple .... il me manque sans aucun doute les bases et aussi le vocabulaire (comme pour toute spécialité)
Merci pour ce travail que vous nous mettez à disposition
jpclerc il vaut mieux reprendre le dessin industriel de base et apprendre a lire le dessin et ensuite c'est une question de langage et de gymnastiques de l'esprits
Il y a les livres des deux Ours qui sont super bien fait pour apprendre la charpente et les épures. Il y a deux tomes sur le trait, et un tome sur le calcul de résistance des matériaux appliqué à la charpente
toitetmoi +1
jpclerc Si votre anglais est bon, vous pouvez regarder schoolofstereotomy.com/. Je sais, c'est étrange de proposer un cours étranger d'un compagnon qui s'est formé en France cependant le cours m'a bien aidé à mettre en pratique ce que j'ai pu lire dans les livres et je n'ai aucun cours du soir ici. Je fais parti de ceux qui ont besoin de structure... Voici un exemple du parcours d'un étudiant : instagram.com/...ereotomy/?hl=fr
Au passage, le tome 3 de la menuiserie qui traite de l'art du trait devrait être rééditer en octobre de cette année.
kevinlebrun Merci pour ces informations
Je vais regarder ça
Bonjour sylvainlefrancomtois. Un énorme merci pour ce partage. Ces informations ne doivent pas se trouver facilement ailleurs, elles sont donc très précieuses!
Je me permets de te poser une première question; comment détermines-tu la longueur des divisions du dôme de pyramide en courbe impériale?
Sur le plein cintre, tu nous invites à diviser en huit parties égales la longueur du demi-cintre. C'est assez facile à calculer. Mais comment doit-on procéder avec le dôme impérial?
D'avance, un grand merci à toi si tu trouves le temps de me répondre.
Amicalement, Baptiste
hello !
il faut tracer ton impérial en "doucine" le profil a l'aide de deux portions de cercle identiques inversés !
puis tu divises chacun en 4 !
si c'est irrégulier, divisions au cheminement ou des altitudes ! mais c'est moins lisible et sujet a des erreurs plus facilement !
Ok, merci infiniment pour ta réponse Sylvain.
Méthode des cordes, division au cheminement, des altitudes...
Je décroche sur ces notions.
Il faut que je cherche encore l'endroit où acquérir ces bases. Une introduction pour les novices complets.
Si quelqu'un a un conseil à ce propos, je suis très preneur!
Baptiste33 y a pas plus simple ailleurs, c'est pour cela que j'ai fait ce pas a pas !
dis moi ou tu butes ?
ci dessous, divisions aléatoires cheminement , et par altitudes !
Merci Sylvain! Je comprends l'idée du cheminement au compas. ce que je ne comprends pas c'est comment tu détermines la valeur d'un pas sans connaitre la longueur exacte de la courbe à gravir. Par altitude, ça me parait plus simple. Tu mesures la hauteur et tu la divises en parties égales. Mais dans ce cas, les "segments" de courbe, les cordes, ne sont pas égales.
Baptiste33 le cheminement se termine avec +/- au dernier segment !
par altitude tu retrouves tes points , sauf qu'ici il faut ajouter le point altitude de rencontre des deux courbes (que j'ai en effet oublié)
essaye les deux, tu aura la même courbe développée .
Ok, je teste toutes ces méthodes! Merci Sylvain!
Salut sylvainlefrancomtois !
Je rencontre un léger problème et je pense que tu pourra y remédier. Quand j'applique la technique décrite dans le tout premier exemple (la pyramide régulière côté) pour tracer la VG et la technique donné dans le premier exemple de la section "angle de corroyage, arête en vrai grandeur, je n'obtient pas la même valeur de VG (le tout pour une pyramide identique de base 500 x 500 et une hauteur de 500). J'ai effectué mon tracé sur logiciel et je n'arrive pas a comprend pourquoi cette valeur est différentes d'une méthode à une autre.
Merci pour tout ton travail sur ce pas à pas !
Lucas.
Lucasprovencal, Sylvain a de gros problèmes de santé, je vais tenter de te répondre à sa place, j'ai une petite maquette pour l'angle de corroyage qui te permettra de visualiser cet angle et la vrai grandeur de l'arête.
bonjour, j'ai pas compris comment coouper les pieds pour qu'ils soit plat et parallèle qu sol ? merci
julian1976 je te communique des documents issus du livre d'André Ricordeau qui je pense te feront bien visualiser le pied en arêtier.
Le livre en question et la façon de procéder par développement du volume pour avoir toutes les coupes sur chaque face (que tu peux faire aussi pour une pièce rectangulaire)
Un autre exemple
merci beaucoup