Déterminer les angles dièdres (angles entre les faces d'une pyramide) peut se faire par le dessin (épure). Mais on peut également les déterminer de manière très précise par le calcul.
On peut le faire grâce à la trigonométrie, mais c'est un peu compliqué. Il existe également une méthode assez puissante, du niveau terminale (c'était au moins le cas il y a longtemps...).
Elle est surtout généralisable au calcul de l'angle dièdre entre deux plans quelconques.
Calcul
Pour cela, on définit 4 points: A, B , C qui sont les sommets de la pyramide "au sol", et D, qui est le sommet, définis par leurs coordonnées cartésiennes.
On calcule les coordonnées des vecteurs DA, DB, DC.
On calcule ensuite les deux vecteurs normaux N1 et N2 (orthogonaux) à (DA, DB), et (DA,DC).
N1 est égal au produit vectoriel de DA et DB, et N2 au produit vectoriel de DA et DC.
Il ne reste plus qu'à calculer l'angle entre N1 et N2, définit par:
cos a = N1 . N2 / norme N1 x norme N2. (N1.N2 est un produit scalaire)
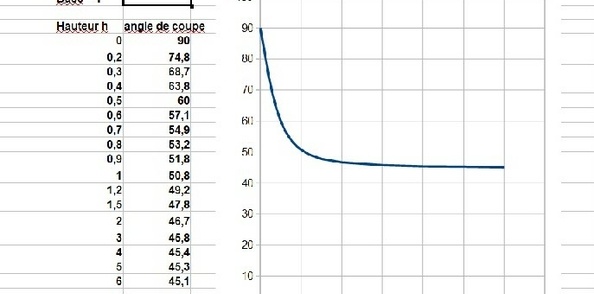
J'ai mis les formules sur un tableur, et j'ai calculé les angles, pour une valeur de 1 pour la mesure du coté de la pyramide (à la base), et une valeur h pour la hauteur.
Voici les résultats (j'ai donné l'angle de coupe, qui est la moitié de l'angle entre les faces).
On remarque que pour h = 0, l'angle est de 90 ° et que pour un valeur un peu importante de h, l'angle tend rapidement vers 45°, ce qui est logique.
On a également la valeur remarquable de 60 ° pour une pyramide où la hauteur est la moitié de la base (quand la pente des faces par rapport au sol est à 45°)
Pour des valeurs intermédiaires, il suffit de faire une approximation linéaire (moyenne, règle de trois).
Le fichier téléchargeable de calcul général (angle entre deux plans) est dans la section Plans
Licence
Discussions
pour pyramide à base rectangulaire je prefere la methode rabattement d'arêtier devoyé avec le petit coup de compas par epure ou trigo
Merci pour ton commentaire. Chacun ses méthodes, mon ami... ;)
Je viens de faire les calculs pour une pyramide à base hexagonale, et dont le sommet n'est pas centré (décalé vers le coté). Donc, rien n'est symétrique. Cela m'a pris moins de 5 minutes, le temps de rentrer les données pour avoir les 6 angles dièdres, les 6 pentes, et les dimensions de chacun des 6 triangles. Et sur ma feuille de calcul, je peux modifier à tout instant la hauteur de la pyramide et le décalage du sommet et même faire une base hexagonale déformée.
Je suis très intéressé par voir comment tu ferais par le dessin à la main.
j'ai beaucoup de mes realisations à base de descro etant charpentier d'apprentissage en jeunesse
Oui, c'est possible, bien sur, mais c'est très long, quand on a à déterminer tous les éléments pour les 6 faces... Avec mon petit tableur, il m'a fallu quelques minutes et en quelques secondes, je peux changer les paramètres à volonté (hauteur, décrochage) :)
En trigo (dont je suis grand amateur) le résultat est toujours dépendant de la précision du dessin. Ta méthode, Kentaro n’a pas cette limitation; tu m’as donnéenvie de retourner voir mes cours de terminale. Pour info, moi je suis paresseux alors je dessine mes aretes en 3d sur Autocad et je lis les angles. Le tout en 5minutes... plus l’allumage de Windows grr...
J'aime bien la trigo, moi aussi, mais l'intérêt de cette méthode de calcul, c'est quelle permet de calculer l'angle de deux plans quelconques dans l'espace. Cela peut être pratique (voir ma pyramide hexagonale avec sommet déporté)...
Les logiciels 3D sont pratiques, mais ce qui me gène avec tous ces logiciels qui facilitent la vie, c'est que cela transforme le monde en un troupeau de beta, avec par derrière quelques alpha qui connaissent les formules et les rentrent dans le code... Je n'aime pas trop me sentir un beta... ;)
Kentaro: oui j’ai vu la pyramide
. On est toujours beta sur quelquechose. C’est vrai que les logiciels nous évitent de calculer, mais les méthodes de calcul, qu’ont elles effacées? Quelles méthodes étaient employées quand on ne connaissait pas les vecteurs? Il y avait certainement des travailleurs qui trouvaient alors que ces calculs enlevaient froidement la saveur d’un bon ajustage empirique tout à l’oeil... les logiciels 3D ça s’apprend. Avec eux viennent toute une série de nouvelles possibilités, connaissances, machineries... autant de choses qui s’apprennent aussi. On en perd et on en gagne... ce qui est sur c’est que le travail du bois en général en a bénéficié beaucoup: on créé un large gamme de nouveaux matériaux à base de bois et toute une série de technologies pour former le bois, le durcir, le rendre plus souple ou plus fin, le faire résister mieux aux incendies etc. En architecture par example, le bois est un matériau du futur, un matériau haute technologie. On commence meme à imaginer des gratte-ciels en bois...
On est d'accord...
Kentaro
Exact
Trouver une nouvelle applications a ces bons vieux produits vectoriels, ça c'est le genre de truc qui me fait plaisir! Merci!
j'adore cet homme, merci Kentaro