L’esthétique en toute chose ne saurait en rien se réduire à du rationnel, et pourtant ....
Elle détermine ce qui provoque chez nous ce sentiment que quelque chose est des plus agréables et réveille ce profond sentiment du Plaisir.
Cependant, quelle que soit la diversité de nos cultures ethniques ou sociales, quels que soit nos patrimoines génétiques si semblables et pourtant si différents, tous les humains ressentent en grande majorité un plaisir certain devant des mêmes choses qui n'ont en commun qu'un biais de construction, une proportion, un « balancement » qui fera qu’un Mongol pourra tomber en admiration devant le Parthénon, ou bien qu’un Sami ne restera pas insensible au charme d’une commode d’André-Charles Boulle.
Certains mystiques, prophètes, marabouts de romans de gare, égypto-UFOlogues et autres Nostradamusiens ont voulu retrouver ces mêmes proportions partout, y compris dans la nature voire dans les galaxies… ceci ne nous concernera pas.
Je préfère l’approche ludique par les mathématiques qui est beaucoup plus pertinente et démontrable, mais soyez rassurés, la suite de cet exposé destiné à une utilisation simplissime et directe, devra être exploitable par le plus grand nombre en toutes choses, mais en menuise, charpente et ébénisterie tout particulièrement.
Je me dois également vous préciser l’aide apportée par l’article d’un surnommé « Ti-bob » dans LaMortaise.com que je remercie.
Un tableur EXCEL est couplé à ce PAS A PAS ce qui facilitera vos calculs a venir > Tableur ICI
**
Liste des articles
Bien des histoires pour pas grand chose
Le Rectangle d'Or, la Spirale d'Or, le Triangle d'Or, le Pentagone découlent tous du Nombre d'Or !
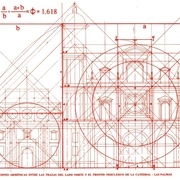
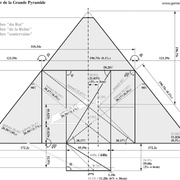
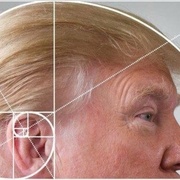
Quelques clichés valent mieux que de long discours...
Ensuite, il est de Divines Proportions qui trahissent l'exceptionnelle Supériorité de l'Homme...
Tous ces millénaires, ces siècles et ces générations d’observateurs et de créateurs pour en arriver à un tout petit chiffre à peine plus grand que 1, et dont le retentissement prétendu se répandra à tout ce que nous avons de plus petit jusqu’aux plus grandes réalisations.
Ce petit chiffre de pas grand-chose : c’est le Nombre d’Or
C'est 1 puis une infinité de décimales après la virgule car c'est un nombre irrationnel transcendant.
Simon Pouffe a déterminé 10 000 000 de décimales en 1998
Désigné par la lettre Phi , je me suis permis de l'arrondir à :
1,61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748475408807586891752126633862223536931793180060766726354433389086595939582905638322661319928290267880675208766892501711696207032221043216269548626296313614438149758701220340805887954454749246185695364864449241044320771344947049565846788509874339442212544877066478091588460749988712400765217057517978834166256249407589069704000281210427621771117778053153171410117046665991466979873176135600670874807101317952368942752194843530567830022878569978297783478458782289110976250030269615617002504643382437764861028383126833037242926752631165339247316711121158818638513316203840052221657912866752946549068113171599343235973494985090409476213222981017261070596116456299098162905552085247903524060201727997471753427775927786256194320827505131218156285512224809394712341451702237358057727861600868838295230459264787801788992199027077690389532196819861514378031499741106926088674296226757560523172777520353613936210767389376455606060626296313614438149758701220340805887954454749246185695364864449241044320771344947049565846788509874339442212544877066478091588460749988712400765217057517978834166256249407589069704000281210427621771117778053153171410117046665991466979873176135600670874807101317952368942752194843530567830022878569978297783478458782289110976250030269615617002504643382437764861028383126833037242926752631165339247316711121158818638513316203840052221657912866752946549068113171599343235973494985090409476213222981017261070596116456299098162905552085247903524060201727997471753427775927786256194320827505131218156285512224809394712341451702237358057727861600868838295230459264787801788992199027077690389532196819861514378031499741106926088674296226757560523172777520353613936210767389376455606060592...Comme Simon, j'en Pouffe de rire !
Dans la pratique, nous retiendrons Phi = 1,618, c'est déjà énorme !
Ce nombre est avant tout un rapport de grandeur, il n’a pas d’unité et peut concerner des longueurs, des surfaces, des volumes, certains arrivent même à le retrouver dans des vers de poésie, de la musique, de la finance, dans la nature et dans l’univers… la liste serait interminable car il me semble que nous trouverons toujours ce que nous voulons absolument y voir, ainsi va la nature humaine.
Si cela vous passionne, allez voir du côté de nos amis mathématiciens, qui lui trouvent des connivences absolument extraordinaires Par ICI les matheux !!!
De très nombreuses expériences ont été faites tendant à soumettre à de nombreux individus d’origine et d’inspiration différentes, un choix de plusieurs rectangles et triangles dont seulement un seul avait ses deux côtés contigus respectant la proportionnalité de 1,618.
Étonnamment, chaque expérience fût-elle répétée sur un bâtiment architectural, une photo, un meuble, c’est toujours ce ratio proportionnel à 1,618 qui emportaient la majorité des suffrages et de loin.
Nos grands maîtres de la charpente, de la menuise et de l'ébénisterie se sont toujours attachés à respecter cette proportion attachée au nombre d’or, peut-être un héritage des bâtisseurs de cathédrales. C’est ce qu'on appelle également la Divine Proportion.
En résumé,
Un rectangle de côté A aura un côté contigu B équivalant à A x 1,618, quelle que soit la grandeur ou l'unité
Peu m’importent les explications, les mathématiques, les démonstrations, les théories plus ou moins fumeuses, les allumés du fantastique et autres fumeurs de moquette… seule l’idée que nous, humains, soyons universellement sensibles à cette proportion me laisse profondément perplexe. Alors, constante quasi universelle, empirisme convergent de l'observation ou conditionnement culturel ?
Donc, si sensibles nous y sommes, cherchons à utiliser le plus souvent possible ce ratio pour flatter l’œil de nos congénères et leur apporter du plaisir.
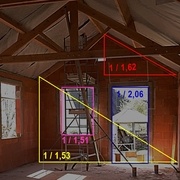
Voici l'exemple de mon futur atelier dont les proportions respectent les différents ratios autour du nombre d’or, pour les dimensions des ouvertures, leur emplacement, les pentes du toit et son dimensionnement global par rapport à la hauteur des murs. Au premier juger, ce n’est pas évident à déceler, mais l’exposé qui suit après vous permettra de comprendre et de voir !
Percevez-vous la proportion ?
UN P'TIT QUIZZZzzzz !
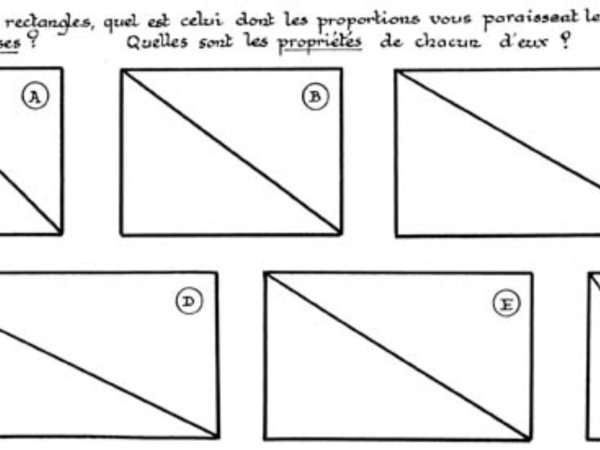
Désignez dans l'image ci-après la forme géométrique qui vous plaît le plus à l'œil !
Essayez également d'en expliquer leur principe de construction trigonométrique.
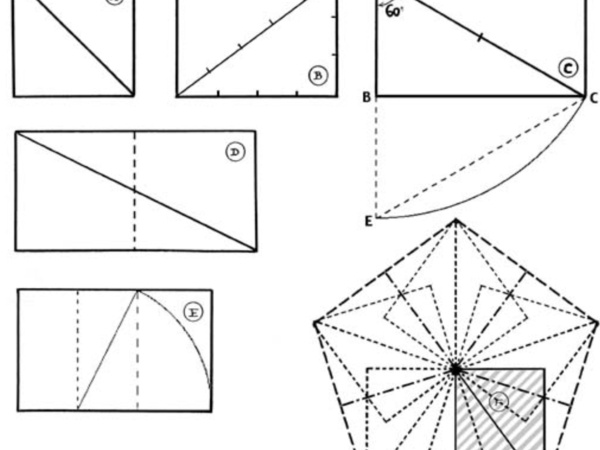
Ces six figures ne sont pas tracées au hasard, mais chacun de ces quadrilatères répond à des proportions bien précises. Et si le rectangle d'or se retrouve bien en E, je vous livre maintenant les caractéristiques des cinq autres.
A est le carré, figure de base ; ses 4 cotés sont égaux et sa diagonale = √2 (1,414)
Dans le rectangle B, la longueur des cotés est respectivement de 3 et 4 ; sa diagonale est donc √(3²+4²) = 5 . Le triangle rectangle 3.4.5 est une figure particulière, qui permet de tracer un angle droit sans disposer d’une équerre, mais simplement avec un mètre, ou même avec une simple ficelle sur laquelle il suffit de faire 13 nœuds équidistants. C"est le prolongement du théorème de Pythagore.
Rectangle C : sa diagonale est égale au double du petit coté ; par conséquent si l’on dessine la figure symétrique par rapport au grand coté, le triangle ACE est équilatéral et la longueur BC = √3 (1,732)
rectangles 2Le rectangle D, c’est le double carré, de proportions 1/2, et qui servira de base à la construction de différents tracés régulateurs.
Enfin le rectangle F nous ramène au chiffre 5, car on le retrouve dans la construction du pentagone régulier, donc de l'étoile à 5 branches ; le rapport de sa diagonale au petit coté est 2/phi. Et on pourrait encore imaginer beaucoup de constructions autour du 5, symbole de la sphère, de la matière et de la vie créative.
Dans la reflexion... par où commencer ?
Passons maintenant à des choses plus pratiques et plus ludiques.
Vous souhaiteriez construire un buffet pour y ranger votre collection de trains électriques ainsi que tout un tas d’ouvrages sur les chemins de fer.
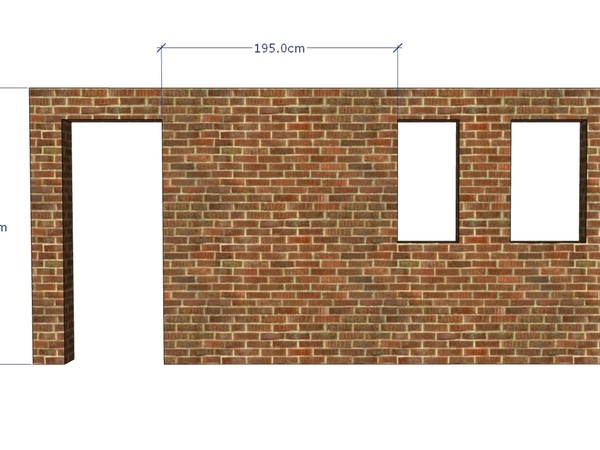
Hélas, votre salon ne possède qu’un seul emplacement disponible, à savoir coincé entre une fenêtre et une porte. Cet espace ne libérant qu’une largeur de 1,95 m. C’est déjà pas si mal, me direz-vous, mais cela dépend de votre passion pour les chemins de fer. Quant au plafond, il est limité à 2,30 m.
Vous aurez certainement remarqué au passage que la fenêtre de droite semble bien plus harmonieuse que la fenêtre de gauche… ah bon ? Comment cela se fait-il ?
Donc nous y voilà :
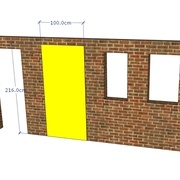
Comment exploiter la plus grande largeur disponible, nous retiendrons ici à 1,00 m tout en restant dans les proportions du nombre d’or et avec un plafond limité à 2,30 m ?
Notre buffet étant comparable à un rectangle, si nous le voulons d’or, il suffit de multiplier la largeur de la base soit 1 m par 1.618 et du coup notre meuble ne dépassera pas 1,62 m…
Pour une collection de poupées Barbie, à la rigueur… et encore suspendue au mur.
Il devient donc évident que si nous restons coincés sur ce ratio de 1 pour 1.618, nous n’irons pas très loin.
L’usage et les mathématiques viennent rapidement à notre rescousse dans le cas présent. Le Nombre d’Or est le point d’orgue d’une série de nombres annexes inscrits dans une suite cohérente de quinze multiples dont la progression reste cohérente et dont voici la liste : NE CHERCHEZ PAS LES CALCULS TRES COMPLETS... C'EST FASTIDIEUX, FAITES COMME MOI COPIEZ-LA !
Série MONTANTE 1,618 / 2,058 / 2,164 / 2,236 / 2,618 / 2,752 / 3,330 / 4,236 / 5,388 / 6,854
Série DESCENDANTE 1,082 / 1,128 / 1,174 / 1,272 / 1,376 / 1,538 / 1,618
Alors oui, autant que faire se peut, il conviendra de rester prioritairement sur le ratio du nombre d’or 1 / 1,618.
Si cela reste impossible à appliquer, il sera tout a fait acceptable de choisir un ratio ascendant ou descendant LE PLUS OPPORTUN dans ces suites montante et descendante pour répondre au mieux à nos attentes et nos contraintes fixées dès le départ du projet. Le résultat restera tout a fait plaisant à l'œil.
Donc, nous désirons augmenter la hauteur de notre buffet à 2 m20. En appliquant le ratio montant 1/2.164 il mesurerait 2,164m, avec 1/2.236 il dépasserait l’objectif à 2,236 m.
Par commodité il est retenu de choisir une hauteur proportionnée à 2,164 m arrondie à 2,16 m.
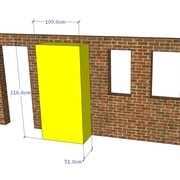
Par la suite, nous aimerions que notre buffet désormais d’une hauteur de 216 cm, ait une profondeur de 48 cm.
L’utilisation des ratios montants nous montre qu’en multipliant 216 par 1/4.236 nous obtenons une profondeur de presque 51 cm et 40 avec 1/5.388. De même, la valeur de 51 cm sera retenue car la plus proche de 48 attendus.
Le tableur Excel joint à cet exposé Pas à Pas, vous permet de déterminer la mesure très rapidement en fonction de vos objectifs.
Pour continuer sur les placards...
Supposons maintenant, que nous scindions notre buffet en deux parties, l’une avec des étagères en partie supérieure, l’autre avec deux portes de placards égales en partie inférieure.
Définir la proportion des portes
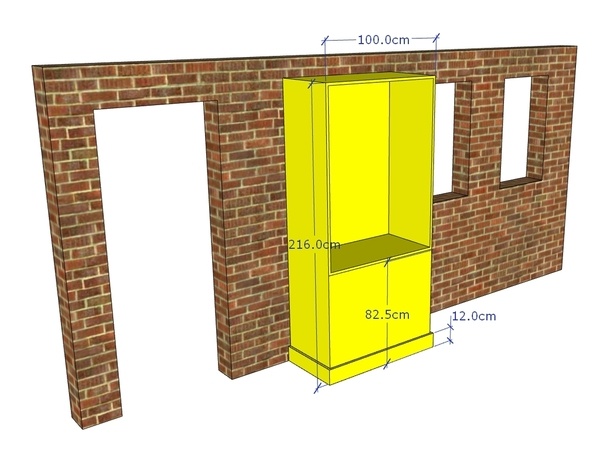
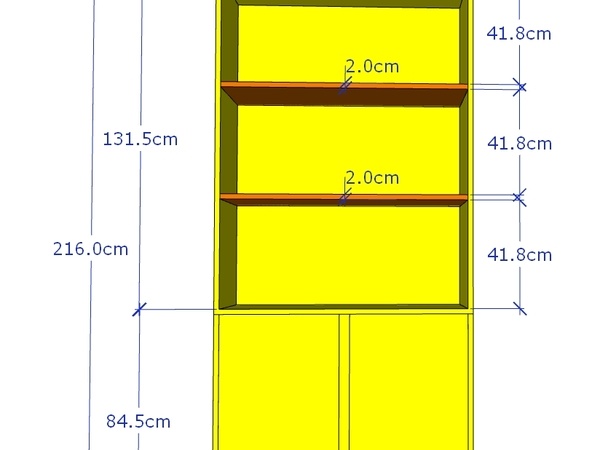
Nous aimerions que la première étagère au-dessus des portes du fait puisse être à une hauteur d’environ 90 cm. Dans le même ordre d’idée que précédemment, nous appliquons à la hauteur du buffet de 216 cm, un des ratios cohérents avec le nombre d’or. L’usage du rapport 1/2,618 nous indiquent une hauteur cohérente esthétique de 82,5 cm.
Supposons maintenant, qu’au bas de ce volume du buffet avec des portes, nous désirions mettre une bande. Sa largeur sera bien de 100 cm augmentés de sa propre épaisseur sur chacun des côtés, sa hauteur peut se définir encore une fois dans la recherche d’un ratio adapté à une hauteur de référence de 82.5 cm maintenant. En retenant la valeur 1/6.854, la hauteur atteindrait 12,03cm soit 12cm.
Les portes, leur hauteur ne devra pas dépasser 82,5-12=70,5cm et leur largeur inférieure à (100 - 2 x parois de coffrage de 2cm)/2=96cm/2=48cm maxi.
Quel ratio adjacent du nombre d’or permettrait de faire entrer en largeur deux portes d’un maximum de 70,5cm de haut et 48 cm de large chacune ?
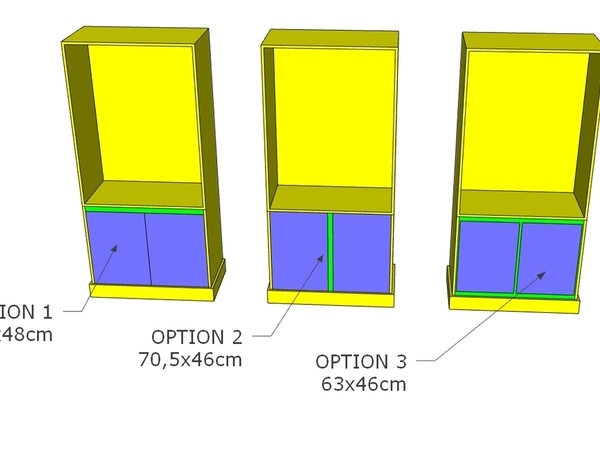
OPTION 1 : Dans la série descendante, 1/1.376 autorise des portes de 48 cm de large mais de seulement 66,05 cm de haut( 66,0cm), il faudra alors ajouter un bandeau supplémentaire horizontal dans la hauteur pour rattraper la différentielle.
OPTION 2 : Dans la même série, 1/1.538 permet des portes d’une hauteur de 70.5 cm, mais au prix d’une réduction de largeur à 45.83 cm, soit 46cm. Il conviendra alors d’ajouter un bandeau supplémentaire vertical entre les portes pour attraper la différentielle de 2 × 46=92 retiré de 96cm de large, soit 4 cm.
OPTION 3 : faire varier les deux paramètres de largeur et de hauteur pour chaque porte. Le ratio 1/1.376 appliqué une largeur de 46 cm donnera une porte d’une hauteur de 63,29 soit 63cm. Il conviendra ce moment-là de rattraper le manque de longueur verticale et horizontale par des bandeaux bien plus modestes !
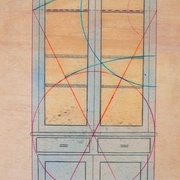
Sur le plan esthétique, vous trouverez ci-après une représentation des trois options. Vous remarquerez qu’à ce niveau de décision, les trois solutions peuvent convenir, c’est là que peuvent entrer en considération les notions de difficulté de construction, de temps passé, de goûts personnels !
Plus c'est simple et épuré, mieux c'est !
Je choisirai l'option n° 2
Pour continuer sur les étagères ...
Voyons maintenant la conception des étagères.
Celles-ci occuperont la partie supérieure de notre buffet.
Deux solutions s’offrent à nous :
• Soit elles sont toutes espacées de façon régulière, ce qui sous-entend que tous les documents que nous allons y ranger devrons avoir une hauteur maximale… ce qui est loin d’être évident.
• Soit on préfère prendre le risque d’un calcul plus sophistiqué consistant à définir un espacement progressivement croissant du haut vers le bas ce qui permettra de ranger plus de documents de tailles différentes.
Tout ceci évidemment dans le respect d’une proportion esthétique reliée au nombre d’or.
REFLEXION PRELIMINAIRE
De quelle place disposons-nous ?
Notre buffet a été consacré en partie basse à des placards à portes battantes ce qui nous laisse au dessus une hauteur disponible de 214 – 84,5 = 129,5cm. La largeur disponible quant à elle est toujours de 100–(2x2cm) = 96cm.Combien voulons-nous d’étagères ?
Considérons les ouvrages les plus grands à ranger sur les étagères qui auront une hauteur maximale de 33 cm, soit 35 cm d’espace libre. Chaque étagère aura une épaisseur de 2 cm, soit un encombrement total de 35+2=37cm par niveau. Notre hauteur utile étant de 129,5cm, nous pourrions bénéficier de 3,39 niveaux. Soit deux étagères espacées en réalité de 129,5 – 2 étagères de 2cm = 125,5cm divisés en 3 niveaux soit un espacement de 41,8cm entre chaque étagère environ. Quelle perte de place ! Et en plus ce ratio 41,5cm/96cm soit 1/0.432 reste très éloigné de la suite logique autour du nombre d’or. Ce sera inélégant au possible. C’est malheureusement ce que l’on observe le plus souvent dans les meubles standards, même vendus par de marques de grande diffusion qui se veulent de qualité !
- La solution va consister en la réalisation d’étagères de hauteur progressive, permettant d’insérer les ouvrages les plus grands (33+2cm) mais offrant plusieurs possibilités de rangement pour les autres documents plus modestes.
CALCUL DES TIOIRS PROGRESSIFS "EN OR"
Nous savons qu’au moins une des étagères devra permettre le rangement d’ouvrages de 33 cm. Par esthétisme et par ergonomie, nous déciderons que ça sera plutôt celle du bas.
Cette étagère d’une largeur de 96 cm, nous la soumettons à la moulinette de notre calculateur Excel associé, et le ratio 1/2.522 peut s’appliquer nous accordant une hauteur libre de 34,9cm suffisants pour les ouvrages de 33 cm.
NB : Le choix optionnel d’un ratio plus élevé à 1/2.058 nous permettrait une hauteur de 46,6cm ce qui serait une perte de place injustifiée et réduirait d’autant la hauteur des étagères supérieures.
Nous savons qu’au moins une des étagères devra permettre le rangement d’ouvrages de 33 cm. Par esthétisme et par ergonomie, nous déciderons que ça sera plutôt celle du bas.
La hauteur pour l’ensemble des étagères progressives est donc de 129,5 cm. L’ensemble comportera quatre étagères donc cinq intervalles entre les étagères. Chaque étagère aura une épaisseur constante de 2 cm. La hauteur nette devient donc 129,5 – (4x2) = 129,5 – 8 = 121,5cm
Si maintenant, chaque intervalle se réduit du haut vers le bas selon le même ratio, nous pouvons établir que l’intervalle du dessous est égal à l’intervalle du dessus x ratio, et vice versa.
Faisons un premier essai avec un ratio appartenant à la suite montante ou descendante du nombre d’or. Prenons le nombre d’or lui-même soit 1.618.
• 1er Intervalle en haut = 1 unité
• 2éme Intervalle = 1x1.618 = 1,618 unité
• 3éme Intervalle = 1.618x1.618 = 2,618 unités
• 4éme Intervalle = 2.618x1.618 = 4,236 unités
• 5éme Intervalle = 3.618x1.618 = 6,854 unités
La hauteur nette devra donc être partagée en un total de 16,326 unités. Chaque unité mesurant 121,5 :16.326 = 7, 44cm.
On s’aperçoit bien que les livres de 33 cm de hauteur rentreront bien dans le 5éme intervalle en bas (7,44 x 6,854 = 51cm) mais 18 cm seront perdus au-dessus des livres. En outre, le premier intervalle en haut n’aura que 7,44 cm de hauteur ce qui est très peu exploitable.
Il convient désormais de modifier le ratio choisi pour optimiser la répartition des étagères progressives. Prenons celui de 1/1.272.
• 1er Intervalle en haut = 1 unité
• 2éme Intervalle = 1x1.272 = 1,272 unité
• 3éme Intervalle = 1.272x1.272 = 1,618 unités
• 4éme Intervalle = 1.618x1.272 = 2,058 unités
• 5éme Intervalle = 2.058x1.272 = 2,618 unités
La hauteur nette devra être maintenant partagée en un total de 8,566 unités. Chaque unité mesurant 121,5 : 8.566 = 14,18cm.
D’emblée, on constate que l’intervalle du bas sera d’une hauteur de 2.618 x 14,18 = 37,13 cm (37cm) suffisante pour accueillir les livres de 33.
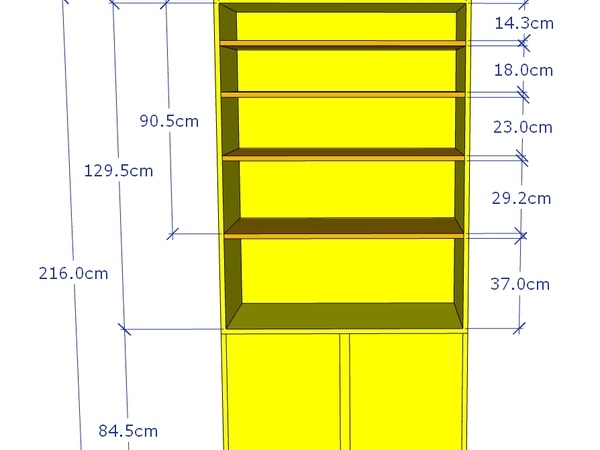
Il convient maintenant d’appliquer les hauteurs respectives de chaque intervalle :
• 1er Intervalle en haut 1 x 14,18 = 14,2 cm
• 2éme Intervalle = 1,272 x 14,18 = 18,0 cm
• 3éme Intervalle = 1,618 x 14,18 = 23,0 cm
• 4éme Intervalle = 2,058 x 14,18 = 29,2 cm
• 5éme Intervalle = 2,618 x 14,18 = 37,0 cm
auxquelles viendront s’ajouter chaque fois une épaisseur d'étagère à savoir 2,0cm.
Perso, je trouve que ça a quand même un p'tit peu plus de "gueule" que les rayonnages d’entrepôts que l’on nous vend à prix d’or pour des buffets de menuiserie !


















Discussions
super pas à pas !!! à suivre !!
Très intéressant
Le nombre d'or aurait pour origine l'analyse des proportions du corps humain, et des proportions qu'on retrouve dans la nature. Autrement dit les constructions basées sur ce ratio seraient une image du corps humain. Ca pourrait expliquer pourquoi ça nous semble familier.
A lire un extrait en anglais :
books.google.f...ion&f=false
Hello,cocotieros
La référence à votre article est très intéressante. J’ai bien lu cet article dont l’origine de la proportion du nombre d’or serait liée à l’observation du corps humain, reproduit dans notre art. Certes, mais alors pourquoi un temple grec est-il beau ? Pourquoi un pavillon de cathédrale ou sa une rosace semblent si harmonieux ? Pourquoi une fenêtre mal proportionnée nous met-elle "mal à l’aise" avec notre œil ? Quel est donc enfin le rapport entre le corps humain par lequel nous serions tant fascinés, et une cathédrale, un tableau ou un arbre ?
Ne prenons-nous pas les choses à l’envers. Qu’est-ce qui nous fascine dans cette proportion pour que nous puissions trouver tant de plaisir à regarder un objet que nous trouvons si bien équilibré, tout en étant si éloigné de ce qui ressemblerait à notre corps ?
Si on pousse un peu plus loin la réflexion sur le lien étroit entre le nombre d’or et la suite de Fibonacci, on observe que celle-ci n’est ni plus ni moins que la représentation mathématique de ce que l’on appelle en biologie la « dichotomie », c’est-à-dire qu’une cellule se divise en deux filles qui elles-mêmes se divisent en quatre petites filles, etc… Tout le règne du vivant se construit de la sorte, depuis la première cellule jusqu’à la constitution d’une feuille, d’un corps humain, d’un escargot ou d’un arbre. Serions-nous, nous même, à ce point génétiquement "imprégnés" par cette loi de multiplication cellulaire basée sur un algorithme de 1.618, que tout ce qui en approche viendrait nous « parler » à l’œil ?
Je n’ai certes pas la réponse mais si certains sont tentés par le sujet, nous pourrions en débattre avec plaisir.
A+
hello , ma réflexion perso !
j aime à penser que l être humain à oublié qu il est un être biologique , et que les instincts primaires naturels enfouis en nous , nous conduisent de fait vers tout se qui serait bénéfique pour la survie comme la solidité , le confort visuel de notre habitat , ( les choses bien proportionnées , niveaux et aplombs , plein cintres , sont gages de sécurité et solidité ) .
Nous sommes tributaire de notre environnement , et recherchons ce qui est le meilleur pour nous y fondre harmonieusement (personnellement et inconsciemment) .
Ok sylvainlefrancomtois, j'entends ta position, mais alors pourquoi cette constance autour de 1,618 dans le vivant, quel qu'il soit ?
je sait pas , dieu ne m a rien dit !!:
sérieusement , c est un mystère qui m a toujours intrigué !!
Très intéressant effectivement ! Merci.
Cependant j'ai bloqué ici :
"L’utilisation des ratios montants nous montre qu’en divisant 216 par 1/4.219 nous obtenons une profondeur de 51 cm et 40 avec 1/5.388"
Ne serait-ce pas plutôt "en multipliant 216 par 1/4.219" ? Ou "divisant 216 par 4.219" ?
De plus d'où sort le 4.219 ? Dans la série montante :
1,618 / 2,058 / 2,164 / 2,236 / 2,618 / 2,752 / 3,330 / 4,236 / 5,388 / 6,854
Alors lequel est faux ? (Ou,et c'est possible, j'ai tout faux moi même ^^)
Oups ! Bien vu, je corrigerai dès que possible...
Je suis impressionné par l'intérêt et l'attention portée à ce dossier.
Merci à vous
Je précise;
Multiplier par 1/x revient à diviser par x
Multiplier 216 par 1 / 4.219 = 216 / 4.219
pour 4,219 au lieu de 4,236, c'est une coquille, c'est bien 4.236
Effectivement mais, en tout cas pour moi en lisant, "diviser 216 par 1/4.219" (ce qui était noté avant correction :) ) ça fait 910 ^^
Il y a t'il une différence entre le nombre d'or et le lingot d'or?
Oui... la proportion !
Maintenant, il me revient que l'on m'a enseigné tout cela quand j'étais jeune, en me précisant : "c'est comme ça". Il ma fallu attendre quelques années et d'autres fréquentations pour que mon caractère schismatique fasse son travail que je me pose d'autres questions.
Si l'on te demande de bâtir une maison sans contraintes urbanistiques, dans ce cas tu peux laisser libre cours à ton imagination et appliquer le dogme géométrique,religieux, politique esthétique..... de ton choix (mais je crois que celui du futur utilisateur est prépondérant) à l'ensemble de l'édifice de la cave au grenier du sol au plafond du tapis à la petite cuillère...
Quittons le conte de fée . Nous sommes sur l'air du bois, ou il est souvent question de meubles j'entends par meubles: table, chaise, étagère, placard,buffet... Qu'on le fasse pour soi ou pour une tierce personne Il est apert de se poser quelques questions sociologiques, techniques, environnementales
(j’emploie ce dernier terme dans le sens ou le nouveau meuble va entrer dans une pièce ou il doit trouver sa place)
-Quel est le futur utilisateur?
-Qui est le futur utilisateur?
-Quel est le besoin?
-Est-ce qu'il y a un programme?
-Est-ce que le nouveau venu fait parti du programme?
-Dans quel pièce va le nouveau venu, est-elle déjà meublée, comment?
-Comment le nouveau venu doit participer au fonctionnement de la pièce?
-........
Il commence à être intéressant de visionner le contenu et d'imaginer une "Vêture" ergonomique, esthétique,fonctionnelle harmonieuse (artistique)....
Si en plus de toutes ces contraintes il s'avérait bénéfique d'appliquer l'enseignement de Euclide.
Pourquoi-pas.
Je ne suis pas convaincu que l'on puisse parler de contrainte car plein de personne réalisent sans s'attacher à faire juste et équilibré, de plaisant à l'oeil d'un majorité ancestrale. Le beau c'est autre chose, c'est perso et influençable ! Il y a tellement de choses dysharmonieuses qui se disent "classe", des créateurs qui font de la daube et qu'il se doit d'applaudir...beurk !!!!
La technique et les contraintes doivent rester discrètes, voire invisibles. Un exemple, l'ère du numérique inonde la planète de 4 milliards de photos chaque jour et les appareils photo font eux-même des retouches automatiques pour des selfies, temples dégénérés de nos narcissismes malades....On ne sait plus construire une image, jouer avec les couleurs vraies, la lumière... ce sont Google, Windows et Apple qui feront l'esthétique de demain ?
complètement d accord avec toi ;)
Excellentissme topo!
Par contre, je ne suis pas trop certain de l'universalité du sentiment esthétique lié au nombre d'or.
Par exemple, toute l'esthétique architecturale japonaise est liée à une brique simple, les dimensions d'un tatami. Or un tatami ne suit pas le nombre d'or. Et pourtant, un temple ou une maison japonaise sont... "parfaits"...
A mon sens, il s'agit plus d'une question de culture. Nous sommes depuis la plus petite enfance formatés, et nous répétons les "cadres". Dans une autre culture, nous réagirions différemment.
Et mettre une spirale sur n'importe qu'elle forme de la nature a posteriori est assez facile. D'autant plus qu'il y a une infinité de spirales différentes. La spirale de Fibonacci, par exemple, est différente de la spirale du nombre d'or, qui n'en est qu'une approximation.
Tu as certainement raison !
Je voulais souligner le côté "collectif" de nos attraits. Le mot universel m’est venu d’une expérience réalisée par choix du plus beau rectangle parmi plusieurs. Que ce soit un inuit, un Européen, un sud-africain ou yéménite, la proportion statistique qui a été retenue dans tous les cas de figure était celle de nombre d’or ! Des Japonais étaient-il présents dans ce test ?
Le débat reste ouvert mais ce n'est que secondaire, seul le plaisir des yeux compte.
Bonjour,
Tombé sur ce pas à pas très intéressant par hasard, les séries alternatives montantes et descendantes m’intriguent. Je sais c’est écrit en majuscule de ne pas chercher le calcul ... mais c’ Calculé comment ?
Je suis navré de n'avoir jamais trouvé la suite algébrique, certainement en rapport avec suite de Fibonacci = une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent 1, 2, 3, 5, 8, 13, 21, etc. J'ai trouvé ces ratios du nombre d'or dans le livre suivant.
Bon courage mais cela vaut vraiment le coup !!!
...
Merci pour ta réponse. Je vais fouiner un peu, drôle de suite car les nombres sont proches les uns des autres.
DewhitYoussef PS si tu trouves la formule algébrique, pourrais-tu me la faire passer ?
SVP Merci A+
Bien sûr! mais c'est pas gagné!
Bon, dans la série montante il y a la progression en puissance par pas de 1/2 avec quelques vilains canards qui viennent s'intercaler à 2,1 2,3 & plus haut. On s'en rend compte car le ratio 1,27... revient souvent quand on fait le rapport de deux termes successifs.
Dans la série descendante, on retrouve les puissances<1, 1/2, 1/3... pas 1/5, peut être 1/6. A nouveau de petits perturbateurs.
Peut être que la suite se base sur un principe de progression plus complexe qui permet de tomber sur les valeurs pour lesquelles je n'ai pas d'explication. ou peut être que le gar s'est dit que ça l'arrangeait bien d'avoir des coefficients complémentaires... ??!
Là encore un ratio de 1,04 1,05 est assez récurrent dans ces cas là.
Bien vu !!!
Bien vu !!!
Tout ça dit, je ne peux quand-même que me faire la réflexion qu'aux chiffres, on leur fait dire ce qu'on veut :stuck_out_tongue_winking_eye
Je reconnais qu'avec phi, on a de belles proportions, mais on se retrouve captifs d'un dogme, c'est dommage. Pour le contemplatif que je suis, trouver dans mon environnement des arrangements qui me plaisent et bâtir autour de ça en reprenant d'une manière un clin d'œil à l'inspiration de base me convient mieux, même si j'applique plus ce concept à mes dessins qu'a mes réalisations bois... pour l'instant. Mais peut-être que phi se cache derrière tout ça quand même.
DewhitYoussef J'ai trouvé ça: images.math.cn...l?id_forum=8100 je sais pas si tu es tombé dessus.
Info ou Mytho ?
youtube.com/wa...h?v=wGEFMXRoa5Q
Peu importe, c'est surtout pas ici un sujet de polémique, c'est beau à l'oeil et puis c'est tout, na !