Le flambement

Revenons brièvement sur le flambage Eulérien que l’on apprend à l’école, et qui existe depuis 2,5 siècles.
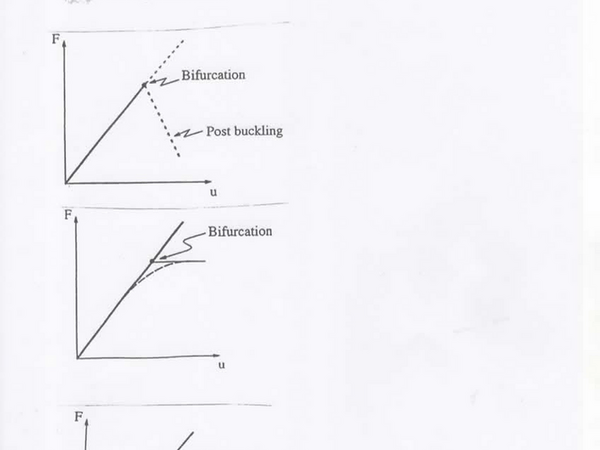
Cette formulation est basée sur la recherche de valeurs propres et de modes à droite et détermine les points de bifurcation de la courbe donnant les chargements en fonction des déplacements d’un point. La structure suit dans un premier temps une courbe de chargement linéaire jusqu’à la charge critique, puis une autre courbe après flambement. Ce type d’analyse est très académique et ne place généralement pas en sécurité. Il ne tient pas compte des non linéarités et des imperfections. Le comportement post flambage est totalement inaccessible. Par contre cette méthode est justifiée pour des structures élastiques et linéarisables, et de plus une étude plus détaillée du comportement après bifurcation peut donner des estimations raisonnables de la charge critique réelle avec des imperfections.
Le flambement est donc une bifurcation d’équilibre avec perte d’unicité de la solution à partir d’une certaine charge.

Pour aborder réellement le flambement il faut considérer ce qui se passe dans une structure qui se déforme. Les mathématiques montrent que la déformation n’est pas proportionnelle aux déplacements, il y a une partie linéaire et une partie non linéaire qui existe aussi. Les résultats sont très différents si l’on considère cette non linéarité géométrique, la loi de comportement étant toujours linéaire en première hypothèse.

Enfin il y a aussi la loi de comportement qui est non linéaire : élastoplasticité, fluage, viscoélastoplasticité…..
Cette partie est assez complexe car il faut tenir compte des écrouissages (isotropes, cinématiques, à variables internes… ) et de tout le processus. Une chose particulièrement importante est le critère tridimensionnel de plasticité. Il définit un domaine dans l’espace des contraintes à 3 ou 6 dimensions, à l’intérieur duquel toute variation de contrainte n’engendre que des déformations élastiques ; Le moyen le plus simple pour mettre en évidence ce domaine est d’utiliser des essais de traction, de compression, de torsion. Ce domaine n’est malheureusement pas convexe et nécessite plusieurs procédés d’analyses numériques. Il existe plusieurs critères de plasticité, citons le critère de Mises, de Tresca, de Drucker, et pour le bois le critère de Tsai.

Ce dernier critère permet de considérer les différences éventuelles d’état d’écrouissage en traction et en compression. Avec toutes les simplifications nécessaires, il reste la détermination expérimentale de 8 coefficients pour aboutir à ce critère en direction des fibres du bois. Ceci nécessite des essais de traction, de compression et des essais de cisaillement dans différentes directions. La plasticité dans le bois ce sont en fait les fibres qui glissent les unes sur les autres.

Il faut à peu près deux années avant que l’esprit se forme à cette théorie, et l’analyse numérique est des plus complexe (analyse implicite aujourd’hui, après environ 12 ans d’erreurs avec l’explicite….mais qui donnait tout de même des résultats).

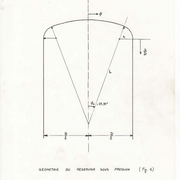
Mais n’imaginez pas que l’élastoplasticité est un truc qui ne se rencontre jamais. J’ai calculé un réservoir sous pression en 1982 et il s’avère que lors des essais la care est entièrement plastifiée (j’aurai du dire élastoplastifiée car plastifiée seulement cela n’existe pas sauf dans les cas académiques). On remarque que la care est en compression d’où le risque de flambement.
On l’utilise aussi avec les métaux : le clinchage par exemple.

Au total donc on a des non linéarités géométriques et des non linéarités dues à la loi de comportement et je le souligne nous ne sommes qu’en petites déformations. (en grandes transformations beaucoup de choses changent encore). On a donc assez de choses maintenant pour aborder le flambement.

UN premier exemple concerne une poutre en fonte GL puis GS

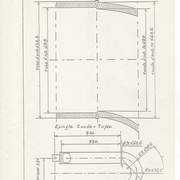
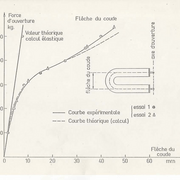
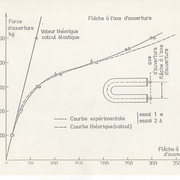
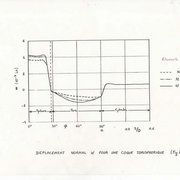
UN deuxième exemple concerne un tube en U

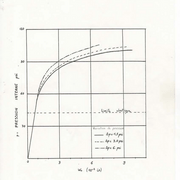
Le troisième exemple concerne un réservoir sous pression réel calculé avec le code ASME et recalculé en élastoplasticité.

Je reviens brièvement sur le flambement qui est une instabilité donc un phénomène dynamique. La théorie des oscillations non linéaires, objet d’études incessantes et fructueuses depuis plus d’un siècle, inspiré dès l’aube de son développement par les écrits savants de Poincarré et Lyapounov (1892) et amène à des résultats tellement disparates qu’une solution industrielle n’a pas encore été atteinte (et après avoir passé pas mal de temps la dessus je pense que ce n’est pas demain que l’on obtiendra satisfaction) Et pourtant cette instabilité se produit dans les avions et dans beaucoup de machines industrielles. Les différents auteurs (une multitude) se sont souciés de leur assurer des fondements mathématiques très solides et d’effectuer plusieurs vérifications expérimentales.

Et pourtant la recherche de condition nécessaire et suffisante de stabilité pour un système dynamique est vraiment un problème mathématique très intéressant. Le premier résultat est dû à Lyapounov . Ce théorème donne pratiquement une condition nécessaire et suffisante de stabilité. Le problème de la stabilité se ramène donc à chercher une telle fonction (dite fonction de Lyapounov) souvent par tâtonnement.
L’écriture d’une autre condition pratique nécessaire est dû à Hale en 1969. Ce théorème fait appel à de difficiles conditions topologiques mais permet de résoudre le problème de l’instabilité.
Ceux qui désirent se lancer dans ces écrits (Hill, Poincaré, Lyapounov, Bolotin, Koiter….) doivent être vraiment « amoureux » des mathématiques, mais ça vaut le coup c’est passionnant.

Pour vous montrer à quoi l’on arrive avec un suivi des conditions stable et non stable je vais donner quelques exemples simples.
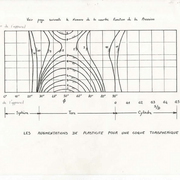
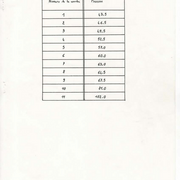
Le premier est un fil dans lequel la force de traction change brusquement suivant le dessin. On fait l’essai avec un fil, portant une masse en son milieu et avec un diapason au centre pour avoir l’amplitude de vibration. La variation d’élasticité (qui se produit souvent dans les structures) du fil consiste en une ondulation qui se superpose à la contrainte élastique et l’on peut déterminer les régions stables (ombrées) et non stables (sans hachures).
On voit que si l’on veut aller de O à A on passe par une multitude de régions non stables donc on aura de très fortes vibrations. On peut réduire le coefficient angulaire de la droite OA ce qui revient à réduire la variation d’élasticité

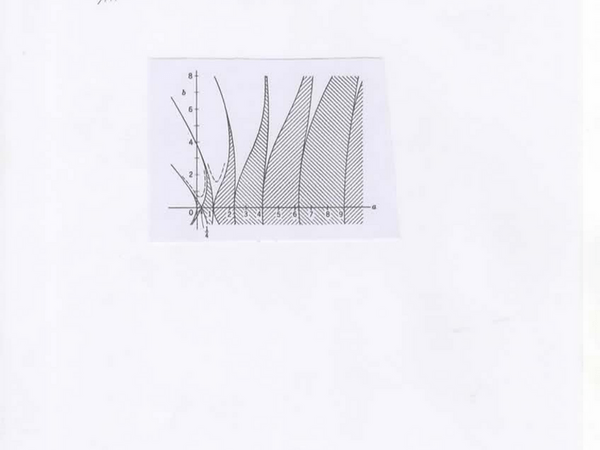
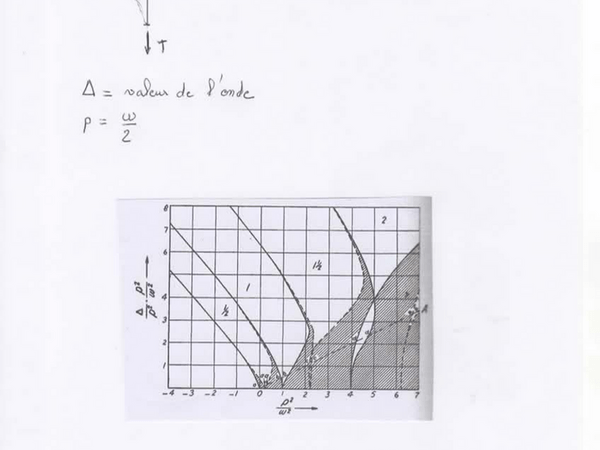
Le second exemple est une poutre soumise à des forces axiales variables.
Pour de faibles valeurs de s nous sommes pratiquement au niveau de l’axe horizontal et l’on s’aperçoit qu’il y a instabilité pour a = ¼, a= 1, a=2 +1/4…….

Donc tout ceci pour dire que la formulation exacte est loin d’être évidente et que la solution industrielle n’existant pas, on calcule donc le flambement statique qui lui n’est qu’une condition nécessaire de flambement mais n’est pas suffisante. La condition nécessaire est l’annulation de la seconde variation virtuelle de l’énergie potentielle totale. C’est le critère de l’énergie.
On va regarder quelques courbes charges déplacements typiques.

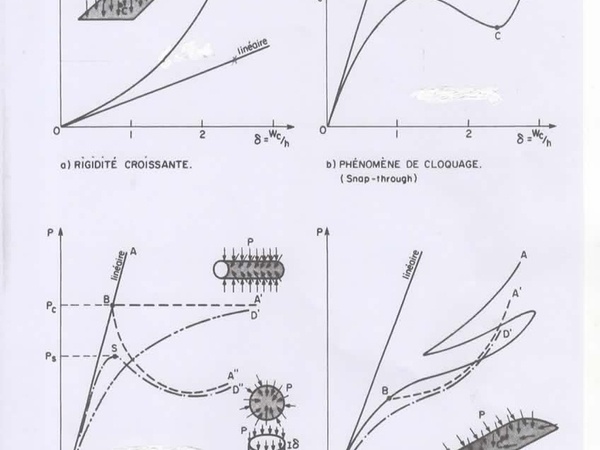
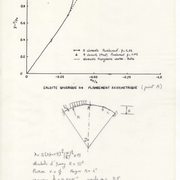
La première image (a) correspond au cas d’une plaque chargée transversalement. La rigidité croît avec la charge appliquée et il n’y a pas de flambement. La courbe charges-déplacements est monotone croissante. On trouve ce phénomène dans différentes coques en particulier des paraboloïdes hyperboliques ;

La figure (b) est typique du flambage de coques (snap through). Que l’on rencontre avec des plaques avec déformations initiales, cylindres, arcs. Ici c’est une coque surbaissée avec une charge appliquée à son sommet. La courbe OBCDA est le chemin d’équilibre fondamental ou primaire. Le point B est le point de cloquage. Les portions OB et CA correspondent à des états stables alors que BC est instable. Il faut savoir que l’on peut obtenir une charge critique pour un déplacement maximum de l’ordre de l’épaisseur seulement.

La figure (c) est caractéristique des flambements linéaires, ou le comportement avant flambement est linéaire. La ligne OBA caractérise le chemin fondamental et le point B est le point de bifurcation. La courbe BA’ (cylindre circulaire infiniment long soumis à une pression uniforme) et BA’’ (sphère complète soumises à ,une pression extérieure uniforme ou cylindre circulaire en compression axiale) sont les chemins secondaires ou courbes post- flambement. La courbe OBA caractérise pour ces coques un comportement axisymétrique alors que les courbes BA’ et BA’’ caractérisent des comportements asymétriques avec un certain nombre de vagues le long de la circonférence. Le point B délimite ainsi deux types de configuration.
Le cylindre circulaire soumis à une pression externe n’est pas sensible aux imperfections pourvu qu’il soit suffisamment long. De petites imperfections de forme, de matériau, de chargement, de conditions limites modifient peu la valeur de la charge critique Pc. La courbe OD’ tenant compte des imperfections tend asymptotiquement vers BA’. Au contraire la sphère soumise à une pression uniforme ou le cylindre en compression axiale sont des coques dites sensibles aux imperfections . Le point B est un maximum théorique qui n’est jamais atteint en pratique. La pente de la courbe post flambement au voisinage de Pc est négative. En tenant compte des imperfections on obtient la courbe OD'' qui passe par un maximum S caractérisant un point limite et le flambement est du type cloquage. Donc il faut retenir que pour certains flambement il est nécessaire d’adjoindre une imperfection que l’on retire en final….encore un truc important de l’analyse numérique .

La figure (d) donne l’allure de la courbe P-déplacements pour un cylindre surbaissé soumis à une pression uniforme externe. Le problème est très fortement non linéaire ainsi que le montre la courbe OA ou l’on note plusieurs déplacements possibles pour un même déplacement ou pour une même charge. Sur la courbe fondamentale symétrique existe un point de bifurcation B origine d’un chemin secondaire adjacent et stable qui caractérise des configurations post flambement asymétriques stables. Cette coque n’est pas sensible aux imperfections ainsi que le montre la courbe OD’ qui ne présente pas de maximum.

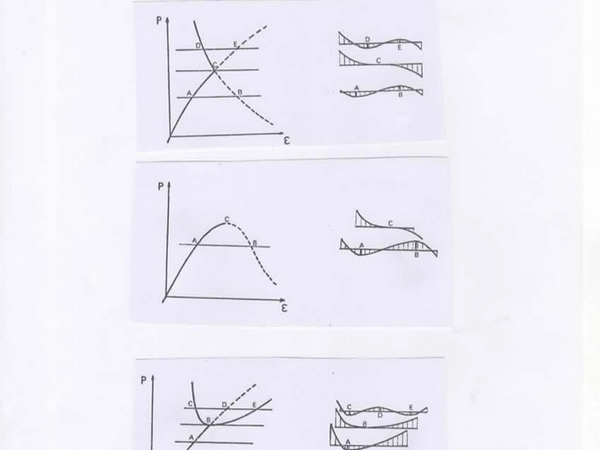
On peut regarder pour divers niveaux de charge les diverses représentations schématiques de l’énergie totale en fonction du paramètre de déformation. Les positions stables sont en traits pleins alors que les instables sont en pointillés. Aux positions stables correspond un minimum relatif de l’énergie, aux positions critiques l’allure de la courbe est très variable : elle peut présenter un minimum, un maximum, ou un point d’inflexion. Le point critique peut donc être stable ou instable. Pour tracer ces courbes il y a bien entendu beaucoup d’analyse numérique. Quand on a l’habitude c’est simple mais sans habitude c’est complexe.

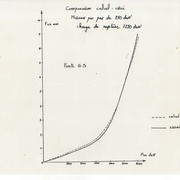
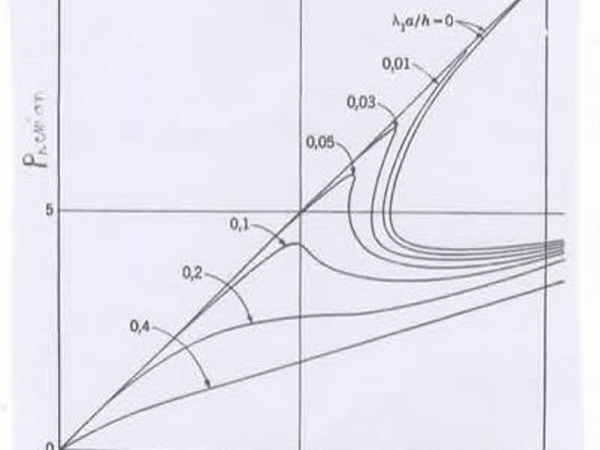
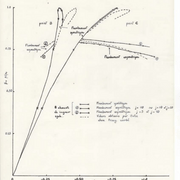
Le premier exemple est le flambement d’une enveloppe cylindrique sous l’action d’une pression latérale, provenant de l’extérieur. A représente le rayon du cylindre, h l’épaisseur de l’enveloppe et λ un facteur numérique. On se rend compte que la pression critique baisse en fonction du rapport a/h jusqu’à ne plus flamber.

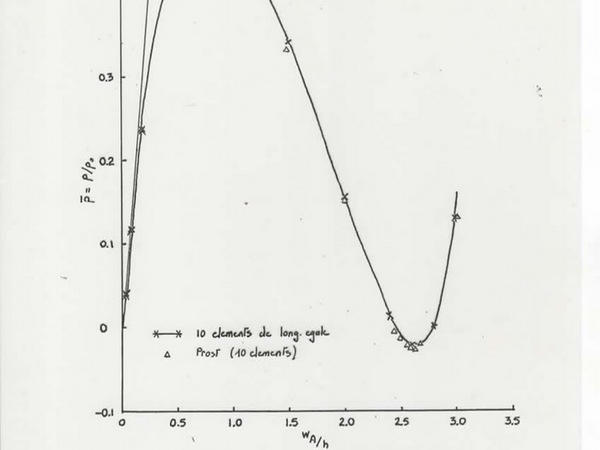
L’exemple suivant est une calotte sphérique S2, simplement supportée et soumise à une pression extérieure normale et uniforme. Il faut revenir aux calculs de cette époque. Les ordinateurs n’avaient pas la puissance qu’ils ont aujourd’hui (et ce n’est rien si l’on suppose la puissance de l’avenir) il fallait trouver un truc pour pouvoir réaliser de tels calculs rapidement. On avait donc crée un élément fini assez spécial basé sur les séries de Fourier, ce qui revenait à effectuer des calculs en 3 dimensions avec seulement un problème en 2 dimensions. On arrive ainsi à calculer une coque avec 10 éléments finis de Fourier. Génial oui mais extrêmement difficile de trouver les harmoniques désignés par j dans les deux exemples suivants (calotte S2 et calotte S4).

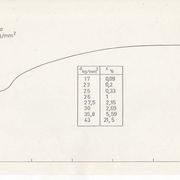
On en vient à la coque S4 et l’on trouve son flambement avec une charge critique adimensionnelle de 1,01 . Cette coque était modélisée avec 8 éléments ce qui est un exploit. Son flambement axisymétrique est obtenu avec une charge critique de 1,01 l’étude de son flambement asymétrique est d’abord obtenu avec l’étude du fondamental et des harmoniques. D’abord avec l’harmonique j=10 qui nous a donné une charge critique de 0,792. J’ai ensuite essayé de considérer les harmoniques j= 10 et j=20 mais cela a été identique , puis en plus du fondamental j+=5 et j=10 et on a pu constater quelque différences puisque la pression critique est devenue 0,815 ;
La conclusion de ces essais avec Fourrier est que le couplage de plusieurs harmoniques avec le fondamental entraînait une différence de pression critique mais que le choix des harmoniques était une chose très délicate à accomplir

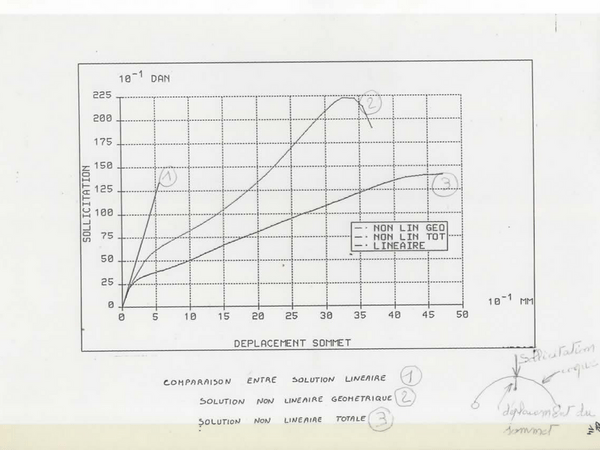
On va maintenant s’intéresser aux comportements des matéraiaux avec non seulement des non linéarités géométriques mais en plus des matériaux élastoplastique, et l’on a analysé une coque (peu importe la description seul le résultat compte) qui flambe élastiquement et élastoplastiquement. La solution élastoplastique est très gourmande en temps de calcul.
Ce qui est intéressant c’est de constater que la solution linéaire ne donne aucun flambement mais que la différence entre le flambement avec une loi de comportement linéaire est extrêmement éloigné du même flambement en élastoplastique. Et l’élastoplasticité elle existe, je l’ai montré.
Alors attention et heureusement qu’il y a des coefficients de sécurité que l’on tente de minimiser.

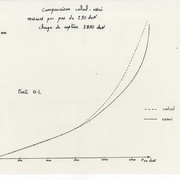
Quelques photos de flambage

Il y a 45 ans environ la théorie du flambement (statique et dynamique) était à la mode, beaucoup d’essais ont été effectués et les résultats étaient en parfaite concordance avec les calculs ( des erreurs de bien moins de 2 %). J’ai donc fait du flambement statique sur des aciers, des fontes, de l’aluminium avec des non linéarités de toutes sortes mais jamais avec du bois ; Pourquoi ? Je ne sais pas ce n’était pas à la mode et puis aussi parce que peu de gens s’occupaient de la théorie du flambage du bois (j’espère qu’il y il y en avait tout de même). Et puis le bois est un matériau comme un autre et toutes les théories de la mécanique des milieux continus s’appliquent à tous les matériaux. On a bien adopté la plasticité du béton !!!
Parmi les nombreux livres que je possède sur cette question et pour les courageux qui voudraient lire un peu plus en profondeur la théorie de Lyapounov je conseille le livre de Maurice Roseau : vibrations non linéaires et théorie de la stabilité 1966 de chez Springer Verlag.

J’espère avoir un tout petit peu intéressé les forumeurs parce qu’aujourd’hui je suis conscient que je suis complétement en dehors des préoccupations des charpentiers, bien que ce soit la réalité et peut être qu’un jour……… !!!!! Il faut aussi se rendre compte que ce forum s’adresse au gens du bois et il y a longtemps que des constructions en bois sont établies, aujourd’hui on fabrique des immeubles en bois, et j’ai même vu le premier sous marin qui était en bois donc obligatoirement on a des problèmes de flambage de poutres, arcs, plaques, coques …..demain….