
Calcul des faces d'un ballon de foot.
Inspiré par les explications de campion et le travail de Steve, merci à eux.
Je me suis amusé a faire quelques recherches pour le calcul des faces et la compréhension du sujet
Un travail d'équipe.
Liste des articles
Vision géométrique
Calculs suivant les indications de Campion
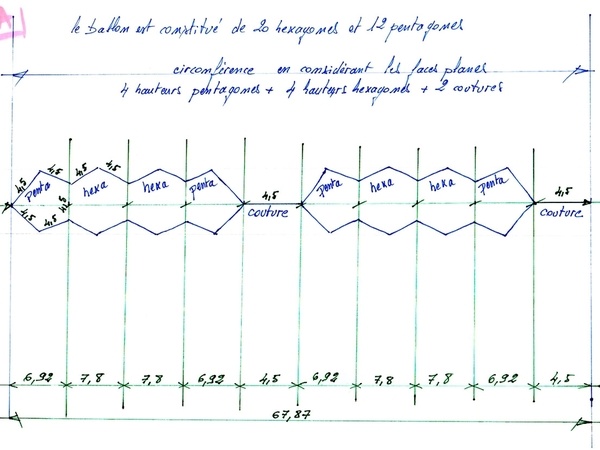
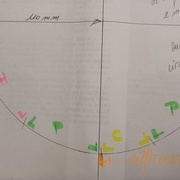
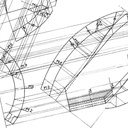
Développement d'une circonférence en considérant les faces planes.
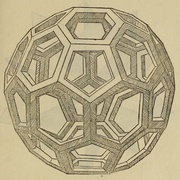
Le ballon est constitué de 20 hexagones et de 12 pentagones.
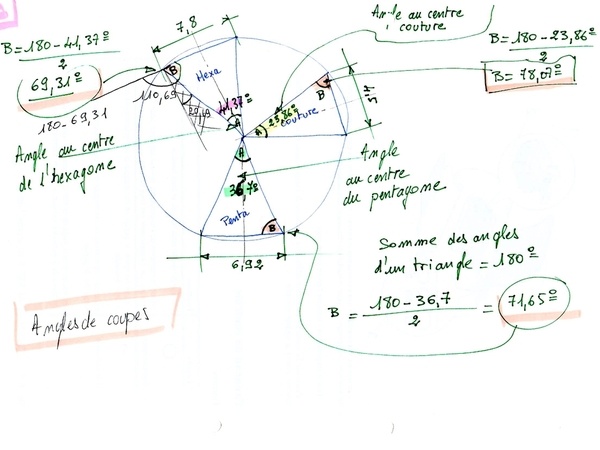
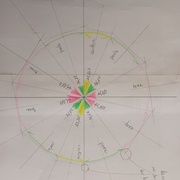
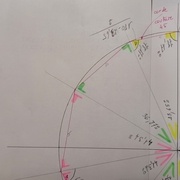
Calcul des angles au centre des pentagones, hexagones et coutures.
En partant de la longueur de la circonférence pour 360° en faisant des calculs en croix.
Calcul des angles de coupes
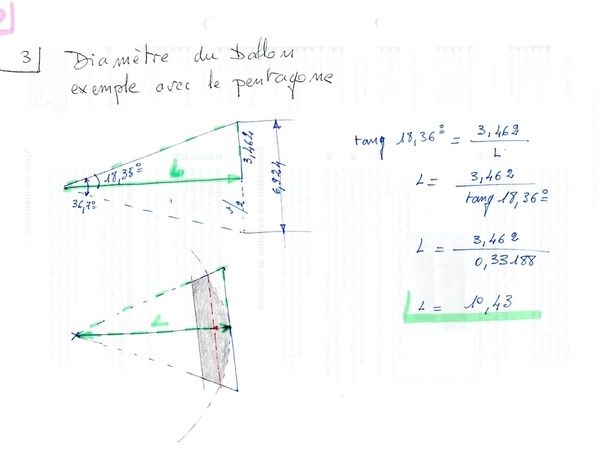
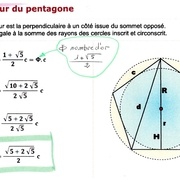
Recherche du diamètre du ballon.
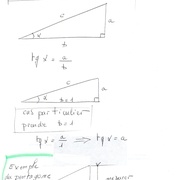
Ici la base du triangle: L
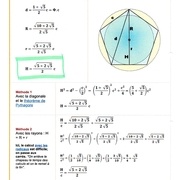
Premier exemple en utilisant le pentagone.
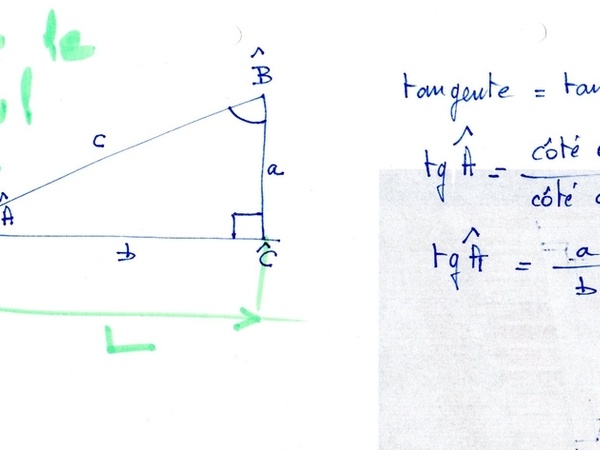
Rappel de trigonométrie pour la résolution du triangle rectangle.
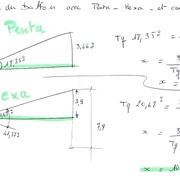
Diamètre du ballon avec le pentagone, l'hexagone et la couture.
On constate des différences du fait de la différence des cordes (minimes)
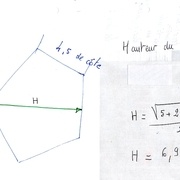
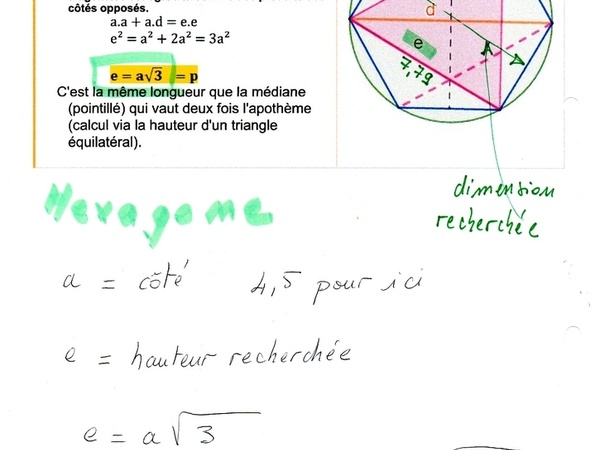
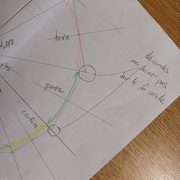
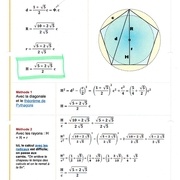
Calcul de la hauteur d'un pentagone.
Calcul de la hauteur d'un hexagone.
Les deux calculs.
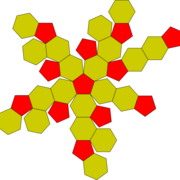
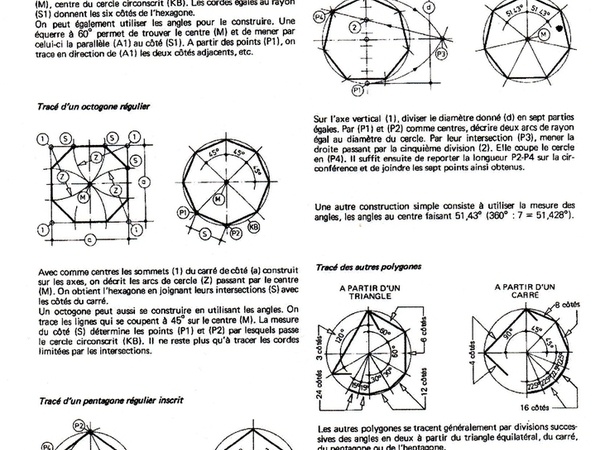
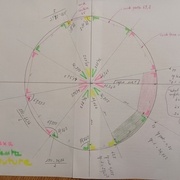
Traçage des polygones réguliers dont le pentagone et l'hexagone.
Les rayons n'étant pas exactement identiques avec des cordes différentes, j'ai cherché une solution pour que toutes les cordes soient sur un même cercle.
Résultat de cette première solution.
Deuxième solution
Solution en prenant l'hypoténuse comme rayon du ballon.
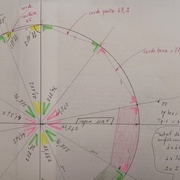
Comment loger 4 cordes d'hexagone, 4 cordes de pentagones et 2 cordes de coutures?
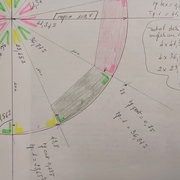
En prenant un rayon moyen des trois hypoténuses: 109.9 pour le pentagone,110.4 pour l'exagone,108.8 pour la couture.
110mm semble un bon compromis pour un essai.
Constatation après cheminement au compas le cercle est trop long de 2mm.
Calcul du nouveau rayon en fonction de cette observation:
Il faut prendre 109.7 mm soit 3/10 en moins ce qui est très minime.
Toutes les cordes sont parfaitement incluses dans ce nouvel essai.
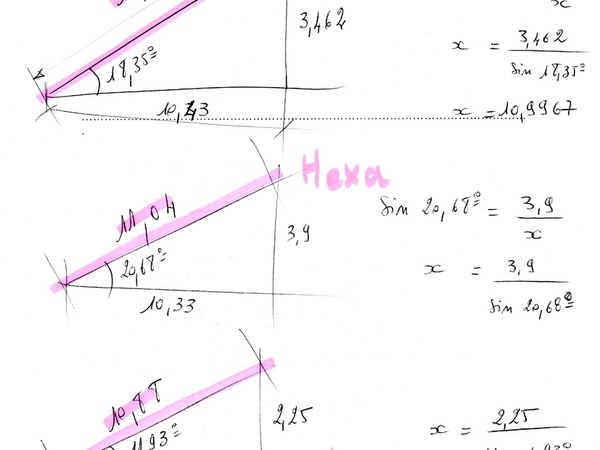
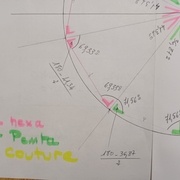
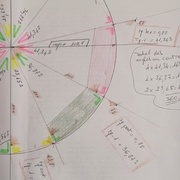
Mesure des angles avec la tangente.
Exemple pour le pentagone:
Mesure de 100 sur le coté adjacent de l'angle.
Relevé sur le côté opposé, ici 75.
Tangente: 0.75.
Tangente -1 : 36.87°.
Observer le triangle et le calcul souligné en brun sur le plan.
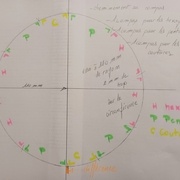
Vérification du total des angles: 360°
Tout les angles sont déterminés et toutes les dimensions peuvent être relevées sur le plan.
Pentagone en vert et hexagone en rouge.
Exposé de Mikaël Le Berre
Je souhaite mettre en valeur cet article de Mikaël LE BERRE à retrouver à partir d'ici dans les commentaires.
Je compare nos résultats ils sont très proches (c'est encourageant).
Dans les deux formules suivantes je cherche à connaitre la signification et la valeur de thêta.
Je trouve la valeur par déduction mais toujours pas la signification.
Je trouve une calculette pour le calcul de la longueur d'arête de l'icosaèdre tronqué compte tenu du rayon médian de la sphère.
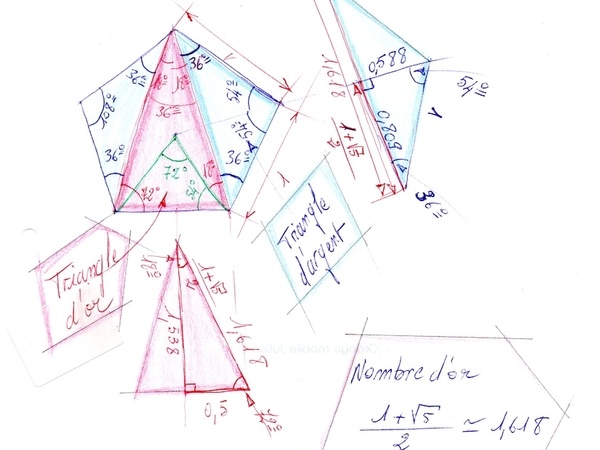
campion me donne la réponse ce n'est autre que le nombre d'or
Conclusion: le nombre d'or ne se cache pas seulement dans le ballon d'or.
Comparaison des résultats
Suite au commentaire de Kentaro ici merci à lui.
Et le lien de ce site
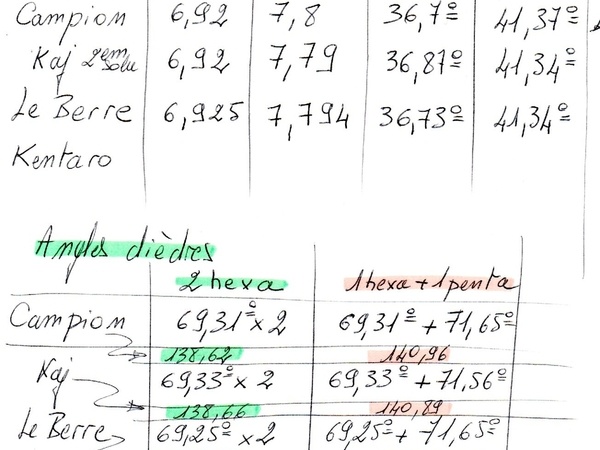
Voici la comparaison des résultats des différents intervenants dans ce pas à pas.
Tout d'abord les copies du site.
Comparaison des cordes, des angles au centre et des angles dièdres
Comparaison du calcul du rayon du ballon.
Tout les résultats sont finalement tous très proches.



























Discussions
kaj
Bravo Jacky.
Des maintenant je me met à la recherche de celui que j'avais fait étant jeune, c'est à dire avant de commencer ma carrière dans le Bâtiment.
Il y a plus de soixante ans
A ce moment là, j'étais passionné par le métal. Surtout l'acier et le laiton.
Je me souviens d'avoir passé un long temps à découper les figures géométriques nécessaires à la réalisation.
Les points de soudure sont faits au TIG.
Il y de cela bien des années, il commençait à présenter une mauvaise mine due à la corrosion
Sans aucune application je lui avais passé un fond de pot d'antiroulle.( honte à moi) Au jourd'hui, grâce à toi il ou elle sort de l,Ombre.
Merci, je cherche le nom de ce polyèdre composé de pentagones et de triangles équilatéraux. Déjà une belle recherche.
kaj icosidodécaèdre.
En géométrie solide, le icosidodécaèdre est l'un des treize polyèdres d'Archimède, obtenus en tronquant les vingt cuspides du dodécaèdre.
merci jacky pour le partage et le temps passé .C'est trés généreux.Kenavo
C'est grâce à ton travail et à celui de Steve ça m'a permis de faire travailler mes méninges
Merci à toi pour ces belles explications. J'avais prévu de rédiger un article sur ce sujet mais tu m'as devancé. Je vais voir pour autant si mes explications sont aussi bonne que les tiennes. Pour les schémas j'ai tout fait sous AutoCAD. Il serait peut-être intéressant que je les publie pour autant. Sinon il faut que je comprenne ton histoire de "couture" que je n'ai pas sur mes schémas. Moi j'avais entrepris de matérialiser les coutures par un simple chanfrein sur chacune des pièces. En tout cas nous avons la même source d'origine, un croquis au tableau de campion, que je remercie aussi au passage.
Mikaël LE BERRE La "couture" n'est autre que la jonction entre les deux pentagones pour le calcul de la circonférence.
Ce serait intéressant de comparer les résultats pour savoir si on obtient quelque chose de similaire.
Bonjour jacky j'ai réfléchi a tes autres solutions,il me vient une question .En souhaitant vouloir le meme rayon,on ne modifie pas la longueur des coutures ?Car il faut me semble t'il que la longueur des coutures du pentagone et la longueur de coutures de l'hexagone soient identiques surtout si on souhaite fabriquer un ballon à facette pour que les face soient à fleur.
Si on conserve les cordes calculées pour des arêtes de 4,5 ( pour les pentagones et les hexagones) il me semble que les faces sont exactes ainsi que les jonctions si on les placent sur la même circonférence.
Seulement mon raisonnement est théorique pour des faces planes, ça demande effectivement à être vérifié en pratique.
Bonjour Jacky. Voici en quelques images les dessins que j'avais préparé sous AutoCAD et sketchup pour la rédaction de l'article. Je suis parti comme toi d'une arrête de 45
on commence par le dessin des formes géométriques. la répartition des formes sur une ligne de périmètre et les formules mathématiques pour le calcul du rayon du ballon.
On voit la progression du positionnement des forme sur le pourtour et les premiers calculs d'angle de coupe et épaisseur de pièces.
Là c'est la visualisation des pièces en plans, la vue éclatée pour le positionnement des languettes et le nombre de pièces différentes à réaliser. J'ai dans le but de faire un puzzle démontable.
Et pour finir les pièce capables avec languette mais je changerai certainement ma technique pour faire des fausses languettes. Ça sera bien plus simple lors de la réalisation. D'ailleurs je prévois d'utiliser un axe comme au centre de chaque pièce qui sera ma référence pour l'ensemble des montages d'usinage.
Pour confirmer mes calculs et plans. j'ai produit un fichier Sketchup reprenant l'ensemble de mes pièces aux cotes. Et une petite maquette avec l'imprimante 3D à l’échelle 1:2 pour vérifier en vrai.
Maintenant y'a plus qu'à trouver le temps à l'atelier pour réaliser les montages d'usinage.
Mikaël LE BERRE cool je regarde tout ça demain
Je compare nos résultats ils sont très proches (c'est encourageant).
Dans une formule j'aimerai connaitre la signification et la valeur de thêta
J'ai trouvé la valeur par déduction mais toujours pas la signification.
J'ai trouvé une calculette pour le calcul de l'arête.
c'est pas le nombre d'or?
campion c'est ça merci
Je confirme. c'est bien le nombre d'or. Je vais prendre le temps de lire tes super retours. Je suis un peu juste en temps en ce moment.
Mikaël LE BERRE Je ne suis pas sur d'avoir tout compris et je réagis un peu rapidement sans avoir été au bout de ma réflexion, mais avec ta méthode, j'ai l'impression que les arrêtes du pentagone ne correspondent pas avec les arrêtes des exagones. Cela n'affleure pas.
D'ailleurs, on le voit dans tes dessins (4ième dessin) et dans le modèle 3D.
En outre, il ne suffit pas de prendre pour le pentagone un rayon différent, car les désagleurs ne sont pas partout pareils.
J'ai l'impression que si on veut quelque chose de précis et exact, il faut prendre les points sommmets définis pas les exagones, et positionner le pentagone pour qu'il affleure partout. De ce fait le pentagone sera légèrement de biais.
D'ailleurs, quand on définit le rayon de l'icosaedre tronqué, c'est le rayon défini par les sommets et pas celui défini par le centre des faces. Les coordonnées de ces points sont donnés ici:
fr.wikipedia.o...osaèdre_tronqué
A partir des coordonnés de ces points, on peut tout calculer facilement, en utilisant le calcul vectoriel (produits vectoriels et scalaires).
Kentaro Le but de mon dessin n'est pas de faire un ballon à facette mais de prévoir les pièces pour avoir un ballon rond par la suite. C'est donc pour ça que les pièces hexagone et pentagones ne se rejoignent pas. Leur position est définie par leur centre (centre du cercle circonscrit) et leur épaisseur par le prolongement de la tangente à partir de ce point.
Par contre ta remarque sur le diamètre d'un icosaèdre calculé à partir de ses sommets est super intéressante. Je n'avait pas pensé à ça. Cela explique certainement mes décalages sur mes premiers calculs. Il va falloir que je reprenne mes supports en conséquence.
Merci pour ces retours super pertinents.
Hello,
Je n'ais pas vu ce pas a pas avant, très intéressante ton étude et comme dab bien expliqué je vais me pencher sur les explications pour voir si je comprends ce qui est moins sur.
Merci Brice, c'est un travail d'équipe (normal pour du foot) étude préalable de campion, exécution de Steve, autre étude de Mikaël LE BERRE et j'ai regroupé tout ça avec une touche personnelle.
Excellent, tu excel dans l'art de la synthèse des études continus comme ça.
Je suis ce pas à pas avec intérêt et en silence. Très bien fait, comme d'habitude.
Je recherche la publication qu'il y a eu sur ce site avec la porte et le ballon (un concours MOF si je ne me trompe pas).
Je ne sais plus si ça a été mis en création ou en trouvaille.
c'est pas la meilleure photo, mais voici à quoi ça ressemble.
Une pointure : atelier-heptagone.fr/
kaj oui je connais le site. Mais je pensais qu'il y avait eu une publication sur l'ADB. Je ne la retrouve pas.
kaj Mikaël LE BERRE Ce document donne tous les éléments concernant la construction d'un Icosaedre tronqué.
mathcurve.com/...e_tronque.shtml
Si a est l'arrête des hexagones et pentagones:
sphère circonscrite (passant par les sommets) : 4,90 x a
sphère inscrite dans les hexagones : 4,53 x a
sphère inscrite dans les pentagones: 4,65 x a
angle dièdre entre 2 hexagones: 138°11'
angle dièdre entre 1 hexagone et 1 pentagone: 142°37'
Kentaro Merci, je vais comparer avec mes résultats
Bonjour,pour la théorie c'est ok.Pour la fabrication , j'usine les pentagone et les hexagones en diminuant légèrement le rayon. si bien sur, je fais un joint creux pour les jonctions.Cela fait plus réel, on a ainsi l'impréssion que le ballon est bien gonflé
Merci pour cette conclusion vu que tout est parti de tes calculs, je me suis un amusé à couper les cheveux en quatre