Hello !
Voici des plateaux en chêne et noyer. J'avais imaginé qu'on peut s'en servir pour se déposer ses clés en rentrant chez soi par exemple.
J'ai tout fait avec ma scie sous table et une ponceuse.
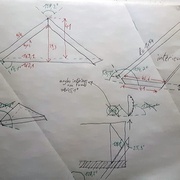
Quelques images de la fabrication :
Ils sont inspirés de ceux-ci, de Kenichi Mizushima, trouvés sur le net. J'ai changé l'hexagone pour un pentagone, histoire de 
Je crois que j'en ai fait 6 en tout, en changeant de bois, de dimensions, de plans...
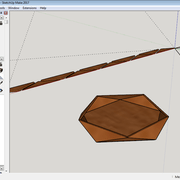
J'ai posté la dernière version de mon plan Sketchup dans la section plans.
C'est pas trop difficile à faire (ça s'assemble comme une boite), mais il faut les bonnes dimensions et les bons angles, donc le plan est plutôt indispensable.
Merci de m'avoir lu et bons copeaux ! 

















Discussions
Très joli boulot !!
J'aimerais bien tenté le coup mais ça doit pas être si simple
Merci ! C'est pas compliqué mais il te faudra le plan :
Tu commences par couper une longue languette de bois à la largeur et épaisseur nécessaire, puis tu la profile sur les deux chants aux angles que tu peux mesurer sur le plan.
Puis tu découpes chaque pièce avec une butée de longueur et un gabarit d'angle (à fabriquer).
Tu relies les 10 pièces par du ruban adhésif, tu mets la colle et tu replies le tout comme pour une boite.
Tu termines par coller le fond et l'araser à la ponceuse à bande.
Si tu veux tu peux me contacter par message privé et je t'aide au pas à pas ?
Superbe!
Comment c'est assemblé ? Collage à plat joint?
C'est vraiment très bien réalisé bravo
Oui c'est juste collé à plat joints. Le fond permet de rigidifier l'ensemble.
Nickel pour les apéro!
Je les ai pas trop pensés pour de l'alimentaire mais ça pourrait éventuellement : la seule finition c'est de l'huile de lin.
C'est un plateau DIZAGNE pour poser des choses ELEGANTES et TRÈCHERS ! Pas des vulgaires saucisses d'apéro...
(j'ai faim maintenant)
Nairod moi aussi
Nairod on peut mettre des toasts au caviar...j'ai re-faim...
Bravo, je trouve ces réalisations superbes ! Tu as dû te marrer pour les calculs d'angles ! En tous cas j'aime mieux ton idée du pentagone que celle de l'hexagone : tu te retrouves avec une symétrie sympa entre le fond et le pentagone formé par les arêtes du dessus ! Et puis bon, t'as aussi la proportion dorée alors, juste trop fort.
! En tous cas j'aime mieux ton idée du pentagone que celle de l'hexagone : tu te retrouves avec une symétrie sympa entre le fond et le pentagone formé par les arêtes du dessus ! Et puis bon, t'as aussi la proportion dorée alors, juste trop fort.
Je suis fan, bravo !
Ah merci ça fait super plaisir !
J'ai pas calculé les angles, sinon je serai devenu fou
J'ai fais un plan Sketchup avec d'abord juste les facettes, puis je leur ai donnés de l'épaisseur (c'est la partie la plus dure).
Après il me restait qu'à mesurer les angles et dimensions du modèle.
Le fond et les arêtes du dessus forment tous deux des pentagones identiques, mais décalés (inversés si on veut). C'est la même chose pour l'hexagone.
J'ai pas compris pour la proportion dorée ? Tu parles du nombre d'or ? J'aurais bien voulu mais je ne l'ai intégré nulle part.
Haha, bien joué pour les angles, et merci la 3D :P !
Pour ce qui est de la proportion dorée, sisi tu l'as intégrée, sans t'en rendre compte mais elle est très présente dans le pentagone. Tu peux même organiser un pentagone en "triangles d'or", c'est ce qu'on appelle un pavage de Penrose : les triangles sont isocèles et tels que le rapport d'un côté par rapport à l'autre forme une proportion dorée. Bref, on pourrait en écrire des tonnes, mais Wikipedia t'expliquera cela en détails si ca t'intéresse ;).
Pavage de Penrose
Triangles aux proportions dorées dans le pentagone
Mais bon, attention sur ce sujet, le nombre d'or il faut aussi le démystifier, ne pas "le voir partout", comme beaucoup le font dans les cathédrales par exemple... Enfin, c'est mon avis :).
Hé ben, je savais pas qu'il y avait le ratio d'or simplement à l'intérieur du pentagone ! Je ne les regarderai plus de la même façon maintenant
Je suis d'accord sur "démystifier le nombre d'or", c'est comme voir des spirales de fibonacci partout.
La photo de Roger Penrose debout sur un sol avec son motif de pavage est très classe.
Nairod Un excellent pas à pas.
Ça a l'air bien intéressant tout ça, Merci bien !
Bravo
Tu aurais eu un succès fou avec ce plateau dizagne pour les 5 ans de l'air du Bois !
C'est quoi ? Vous avez fait une fête ou... ?
Il fallait trouver des créations avec le 5 :
lairdubois.fr/...jettabouret5ans
Didier Ah ok ! Où est-ce qu'on peut voir les créations ?
Il n'y en a qu'une.
Tu peux l'ouvrir en cliquant sur la ligne créations
lairdubois.fr/...db_sticker_html
Faudrait refaire la même chose pour les 7 ans, avec des créations heptagonales !
Nairod pourquoi pas !
Reste à trouver 47 volontaires en plus de nous deux ;)
Parce que 7x7=49 ?
Oui, il il avait 5x5 pièces à assembler.
lairdubois.fr/...sticker_preview
46 volontaires :) ! Ca me plairait bien cette idée !
Faudrait faire une liste d'inscris quelque part ? ?
?
Est-ce qu'on peut pas commencer tout de suite avec des/une création(s) (j'ai pas bien compris le concept) hexagonale pour les 6 ans
On pourrait faire un collectif :) !
Si j'ai bien lu (pas sûr ;)), pour les 5 ans un tabouret a été fait :
chaque membre du projet a réalisé une partie, assemblées par un référent pour au final donner l'oeuvre commune. Tu verras mon commentaire dessus, je trouve que c'est la plus belle réalisation de l'ADB !
J'en suis !
Un truc hexagonal pour les 6 ans ? C'est quand la date anniversaire en fait ?
Nairod Tu retardes
Et pour les cinq ans il y a eu ça aussi
ça aussi
Début février... Ça nous laisse un mois et demi pour fabriquer un truc octogonal.
C'est jouable ?
Super les projets !
On pourrait faire chacun une face d'un octaèdre ? Ou diviser chaque face en 4 pour permettre à 32 personnes de participer ?
Ça pourrait faire un beau patchwork.
Ben j'ai créé un collectif et un Pas à Pas pour communiquer, venez poster vos idées !
Trop bien !
J'ai demandé à rejoindre le collectif =) !
Cinq Sens du Bois Accepté !
Cinq Sens du Bois Le chef d'orchestre de ce projet, c'est cereus45
Très sympa ! Je les voyais plus petits et en fait ils sont grands !
Je vois qu'on est nombreux à avoir des ustensiles de muscu... qui servent pour le collage !!!
J'en ai fait en plusieurs tailles différentes.
Je me rappelle encore le jour où j'ai fait 1km à pied du Décathlon jusque chez moi avec cette put*** de valise d'haltères. Au final elles m'ont bien servi mais dans l'atelier
Nairod
wouahouu c'est magnifique !
C'est le genre de truc que je trouve fascinant à regarder : on suit les lignes du regard, on se perd dans les jeux d'ombre, on regarde le fil du bois mis en valeur par tous ces effets. Bravo !
Mais je trouve ça un peu limite de publier aussi près de Noël... on aura jamais le temps de faire les notres pour mettre sous le sapin !
En tout cas merci du partage !
Mais si, t'as tout le temps !
C'est assez "facile" à déterminer les angles sans faire un plan 3D...
Ce sont des calculs d'angles dièdre.
Aah oui mais je connais pas les techniques de l'arêtier. Ça fait longtemps que je me dis que je dois y jeter un œil, parce que SketchUp c'est parfois épuisant (surtout que j'ai pas la fonction "intersecter" car j'utilise la version gratuite)
Merci pour les liens Kentaro , j'avais le premier mais pas le second ! . Nul doute qu'avec ces techniques, je m'en serais sorti avec plus de cheveux
. Nul doute qu'avec ces techniques, je m'en serais sorti avec plus de cheveux 
Et effectivement, sans cette méthode, j'ai déjà fait les calculs pour réaliser un dodécaèdre et je m'étais un peu pris la tête
Pour les solides de Platon, comme le dodécaèdre, l'angle dièdre est inscris sur wikipedia !
fr.wikipedia.o...caèdre_régulier
Bon après faut un peu le transformer (et le diviser en deux) pour avoir la coupe en biseau sur chaque bord du pentagone.
Oh punaise rien que de regarder j’ai mal à la tête d’imaginer la fabrication parce que la je pense à la précision dans les angles et les coupes.
C’est vraiment super beau et original, très épuré. Le genre d’objet qui donne envie de faire.
Beau cadeau de Noël effectivement.
Merci ! C'est vrai qu'avoir tous les angles qui tombent pas trop mal a pas été facile... Mes premiers je les ai "ajustés" à la ponceuse à bande
Après, si on respecte bien les valeurs d'angle et les dimensions, normalement ça s'assemble tout seul. Mais entre théorie et pratique...
Oui c'est très beau !
Merci
Je le réécris ici quand même : j'ai été très inspiré par le plateau de Kenichi Mizushima.
Bravo c’est « simple » et élégant !!!
Merci !
Très belle réalisation, c'est superbe ! Sinon pour le calcul des angles diedres geogebra est très facile à utiliser. Exemple rapide geogebra.org/m/mfrfr2qr
olivimo C'est la même chose que l'appli que j'ai faite et dont j'ai donné le lien plus haut. Et en plus, j'explique comment j'ai fait...
Kentaro oui tout-à-fait d'ailleurs l'exemple est directement tiré de ta description ;-) Je l'ai simplement mis en lien pour montrer que l'on peut facilement retranscrire des problèmes de géométrie avec ce logiciel et il est très facile à prendre en main.
Merci ! Et merci pour toutes vos applis, ça me servira !
Super boulot
Merci !