Une nouvelle colonie ! C'est bien.
Je crois que les abeilles aiment l'authentique("je sais pas ce que c'est de l'authentique!", Ugolin dans Manon des sources).
Très beau. Le style fait penser aux années 70.
Pour la gloire, l'honneur et nos archives, il serait intéressant de faire ce pas à pas, car même si cela n'est plus d'actualité, je serais intéressé de voir cette vielle toupie, même si elle est grincheuse.
Bel endroit et belle œuvre. Bravo.
La charpente a-t-elle été refaite selon le plan d'origine ?
Quel ouvrage conseillerais-tu pour le dimensionnement de charpente ?
J'étais tombé sue un petit fascicule des années 80 qui était bien fait et malheureusement, je ne l'ai pas gardé. Merci.
Merci.
Bonjour,
Une journée portes ouvertes du lycée est-elle programmée ? Merci.
Merci, je viendrai.
Oui, très bien dessiné.
DewhitYoussef N'était-il pas immergé parce qu'il est urticant lorsqu'on le travaille ? Je ne me souviens plus quelle essence est urticante.
Bravo, cela a de la classe. As-tu réalisé le lambris ou c'est une fourniture courante à Yaoundé ?
Merci pour ta réponse.
Au contraire, c'est mieux pour les torche-vignes qui ne savent pas se tenir ! 
BESSIKE Comme les plafond suspendus avec un "lattage" de profilés en alu. Tu passes le carreau de travers, tu le tournes et il vient se poser sur les lattes. C'est cela ?
Essaies avec un petit cercle plus petit.
Allons!!! C'est le cours de la première journée de la première semaine de la première année de CAP dessinateur.
trente six seb Ah, c'est joli.
La solution :
Bonne nuit !
trente six seb Yeah !
dneis Monsieur lit "Les Echos" !!
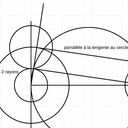
Didier Oui, bravo. Le principe est d'éliminer un des deux rayons.
Didier J'ai imaginé cet exercice lorsque j'encadrais des jeunes dessinateurs qui pissaient des vues dans tous les sens sur CAO, qui utilisaient les fonctionnalités de tracé de tangentes, sans savoir dessiner.
Il y a un autre exercice intéressant à faire, c'est construire un cercle tangent à trois cercles. Tu peux y passer du temps ! 
Je ne connais pas ce nom-là, je me souviens de la construction qui est intéressante à faire.
Il disait quoi cet article ?
Et qu'y a-t-il d'intéressant à l'Abbaye de Borquédan ?
Belle réalisation, c'est très chaud d'aspect.
Je trouve que ces activités participatives sont autant intéressantes d'un point de vue humain et sociétal qu'artisanal.
Le lieu de vente est-il aussi participatif ?
GueulesDeBois Il faudra, en premier, créer des clients.
Il est payé au cercle ou quoi ??? C'est pas lui qui paye l'encre et la gomme.
Coup de bol !
J'utilise QCAD sous Xubuntu qui est simple, mais lourd pour passer d'une fonction à une autre.
Euclid était le nom d'une CAO des premiers temps fournie par Matra-datavision et très utilisé dans l'automobile.
Wikipedia : Euclid est un logiciel de CAO 3D, initié et développé en Fortran par D Jean-Marc Brun au CNRS à la fin des années 1960 puis industrialisé par la société Datavision qu'il fonde avec Alain Nicolaïdis et Michel Théron en 1979. Rachetée par Matra en 1980, la société Matra-Datavision développe le logiciel Euclid puis Euclid-IS puis Euclid-Quantum avec son nouveau moteur géométrique Cascade.
Oui, sans problème, bien que je ne connaisse que le point de départ, je n'ai pas encore tracé.
Une règle en géométrie : il n'y a pas beaucoup de choses à connaître :
1 : le triangle rectangle de Pythagore
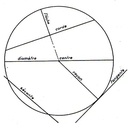
2 : les droite remarquables du cercle :
2.1 le rayon
2.2 le diamètre
2.3 la tangente
2.4 la corde (la sécante infinie porte le segment corde fini)
2.5 la flèche (je ne l'utilise que très rarement)
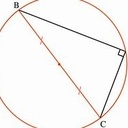
2.6 le triangle inscrit dans le cercle dont l’hypoténuse est confondu avec son diamètre.
et toutes les règles qui en découlent.
Ces connaissances résolvent pratiquement 90 % des problèmes de géométrie.
Les règles qui en découlent :
a - la tangente passant par l'extrémité du rayon est perpendiculaire à celui-ci(de-même pour un diamètre, vous vous en doutez).
b - la bissectrice (droite perpendiculaire passant par le milieu d'un segment) de la corde passe par le centre du cercle.
c - tout point du cercle relié aux deux extrémités d'un diamètre forme un triangle rectangle(2ème et 3ème schéma).
Les règles a et b doivent être suffisantes pour résoudre ce problème.
Les tricheurs gagnent 1/2 point. 
Désolé, je ne trouve pas, je me trouve rouillé.
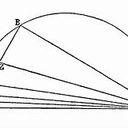
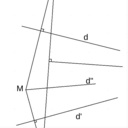
J'ai essayé dans cette voie, en reliant les points extrêmes M' et M" qui sont sur le cercle, cela donne un nouveau segment dont la bissectrice va au cente, mais je ne trouve pas.
M' et M" sont les symétriques de M par rapport aux droites d et d'.
Tu ne dois pas tracer le centre du cercle puisque tu ne le connais pas.
Les parallèles haute et basse sont inutiles et ne donne pas de résultat correct.
Oui, mais considère que c'est hors de la feuille et que tu ne peux pas tracer le centre.
A et B sont à l'intersection des cordes et des médiatrices mais ne sont pas sur le cercle. Ce sont les symétriques de M, M' et M" par rapport aux droites d et d' qui sont sur le cercle.
Positionne les point A et B comme précédemment positionnés pour être sûr que l'on parle des mêmes points.
Bravo !
Le rayon du cercle égal MC':
Abaisser la perpendiculaire de M sur AB :
Tracer un rayon de valeur quelconque centré sur M venant couper AB en deux points M1 et M2.
Planter le compas en M1 et M2 et reporter M de l'autre côté de AB : M3.
Tracer la perpendiculaire à AB en reliant M et M3.
tracer le cercle dont le centre est M et passe par l'intersection de MM3 et AB.
Pour obtenir par tracé le point A' :
Tracer le milieu de MB par le tracé de la médiatrice:
A partir de M et B reporter au compas de chaque côté de MB un rayon quelconque à partir de M et B.
Ces rayons se croisent en deux points qui permettent de tracer la médiatrice de MB.
A l'intersection de la médiatrice et de MB se trouve le milieu de MB.
Tracer un cercle depuis ce point et passant par M et B, le point A' est à l'intersection de ce cercle et du cercle de rayon MC'. pfff !!!!
De même pour B'.
Prolonger BA' et AB' pour obtenir C.
Le cercle est inscrit dans le triangle ABC.
MA, MB, MC sont les bissectrices du triangle ABC.
Pourquoi cela marche ? Je ne sais pas. Un concours de circonstances ?
Tu ne peux pas tracer le cercle car le centre est en dehors de la feuille. Prends le problème depuis le début.
Redonnes un tracé avec les points M, A et B, ça ne colle pas.
Moi, je suis parti du problème posé.
C'est faux ! C'est faux ! C'est faux !
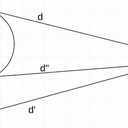
« le mieux est l’ennemi du bien »
Quel dommage ! C'était une belle réalisation. Quelle était la dimension du tronc ?