Nicoel C'est une malle Moynat. Bien plus rare et high class qu'une Vuitton!
On est vraiment entré définitivement dans un monde warholien à la puissance 10 000....
Une banane scotchée sur une malle Moynat, mise automatiquement en exergue sur l'Air du Bois par un algorithme zelokovien parce que le seuil des 15 j'aime a été dépassé...
lamalleencoin Je ne sais pas si tu sais, mais ta Banane est désormais sur Pinterest. Tu vas avoir une gloire interplanétaire! Tu vas être connu même sur Mars! Ton "quart d'heure" est parti pour être une éternité!
Les passionnés qui changent la "boite" de leur ancienne platine THORENS ou LENCO (on appelle cela une "plinth") remplissent au maximum l'intérieur, avec du mdf, par exemple, en faisant des découpes adéquates, de manière à prévenir les vibrations. Il parait que cela change tout.
Il y a des discussions infinies sur les forum Lenco/thorens vintage, pour savoir quel bois utiliser. Certains font des merveilles.
J'avais commencé à refaire une base pour une platine thorens, mais je ne l'ai jamais terminé... Il va falloir que je m'y remette aussi.
Rico29 Pour le voir en fonctionnement, il faut venir observer avec ses yeux. Ce genre de télescope peut faire des photos, certes, mais ce n'est pas vraiment l'intérêt ( les petits télescopes amateurs permettent de faire de très belles photos). Ici, on est sur du visuel, des photons qui arrivent directement sur la rétine. Rien à voir avec les photos. On est ici chez les "poètes".
Par contre, avec ce genre de grand diamètre, on peut voir plein de galaxies situées à plus de 50 ou 100 millions d'années lumières, des couleurs sur de belles nébuleuses, des détails sur les bandes de Jupiter, etc, etc...
Nairod Non, le ELT!
Erebor L'oculaire, est à 2,5m. Il faut donc un escabeau.
Camera, on peut le faire. Mais ce n'est pas trop l'intérêt. Ce genre de grand télescope sert à récolter des photos qui arrivent directement sur la rétine après avoir voyagé pendant des millions d'années. C'est ça la poésie du truc...
sylvainlefrancomtois En 15 ans et 250 télescopes, j'ai eu le temps d'expérimenter pas mal de choses...
Il reste des choses qui ne changent pas:
- Une base sur lequel l'ensemble pivote,
- Une structure triangulée pour la rigidité (8 ou 6 tubes),
- deux bananes qui permettent d'incliner la structure.
Ensuite, tout est possible...
sylvainlefrancomtois J'ai fait des télescopes en cp plein, alvéolés, polystyrène + cp très fin, fibre de verre+ kevlar, impression 3D... J'ai un peu tout expérimenté en terme de matières.
Vernis marine, vernis pour parquets, laques de carosserie.
je voudrais en faire en impression 3D résine/bois.
En regardant les sièges auto pour mes petits enfants, je me dis qu'il faudrait en faire tout simplement en plastique injecté très rigide. Mais les moules coutent bien trop cher pour une production limitée.
mmahieu IL y a 4 pieds réglables en hauteur, qui permettent de soulever l'ensemble et de désolidariser les roues. Sinon, en effet, ce ne serait pas stable.
La structure coûte 11 000 € (dont 8 tubes carbone à 3000 €, un porte oculaire à 1500 €), et le miroir coûte 15 000 €. Les artisans opticiens capables de réaliser des grands miroirs de cette taille (et de qualité) se comptent sur les doigts d'une main dans le monde entier.
LeCongreDebout C'est le prix d'une petite voiture... Certains clients préfèrent acheter une bagnole d'occase à 2000 balles et mettre le reste dans un grand télescope. Ou ne pas partir en vacances aux Maldives. C'est un choix de vie.
Pour la structure, c'est surtout de l'assemblage d'éléments qui individuellement coûtent énormément chers. Personnellement, ma marge sur l'ensemble est faible.
De même, la réalisation du miroir est un truc extrêmement sensible. La précision demandée est de ouf. Les manipulations sont dangereuses. Une rayure sur la surface, c'est 15 jours de travail supplémentaire, etc, etc... Le type bosse dans son garage, et il y a plusieurs mois de travail sur ce genre de choses.
D'où le prix.
AvecUnBoutDeBois Sur les photos, la motorisation n'est pas encore installée.
Pour le positionnement, il y a des 2 encodeurs (comme des codes barres), qui déterminent les angles de pointage, après avoir fait 3 pointages de référence par triangulation.
Ces encodeurs donnent la position, transmise à un boitier électronique, qui pilote les moteurs. Cela permet de trouver une cible, un objet dans le ciel, et de faire le suivi (la terre tourne, donc, les objects se déplacent dans le ciel, comme le soleil pendant le jour).
C'est très précis.
Sur celui-ci, un 600 mm, on voit les moteurs et les encodeurs, sur certaines photos:
Récemment a été développé un autre système: une caméra photographie la portion du ciel où pointe le télescope. Un logiciel de "plate solving" (reconnaissance des objets) détermine où pointe le télescope, et liée à une base de donnée des objets du ciel, indique aux moteurs quels sont les mouvements à faire pour faire le pointage, puis le suivi.
C'est beaucoup plus simple, plus d'encodeurs, plus de cables dans tous les sens, plus de pointage de référence, avec un suivi en réel beaucoup plus précis.
RiGy Le miroir primaire est à F/D 3 (focale de 2,1m).
La structure est sur roulements. Donc, les mouvements sont très fluides. Quand c'est équilibré, il se pilote du bout des doigts. Il faut même des freins, sinon, cela part dans tous les sens.
La motorisation n'est de ce fait pas indispensable. Mais de nos jours, les gens ont besoins d'électronique, de trucs qui leur permettent de se rassurer. Et ils ne connaissent plus leur ciel. Il leur fait des machins sur leurs téléphones pour les aider...
Avec une motorisation, pas besoin de table équatoriale. Par contre, pour de la photo, il faudra un dérotateur de champ.
La jupe de protection anti-lumières parasite est bien sur prévue.
P1ng Le miroir primaire pèse 50 kg.
mmahieu Oui, bien sur, les 8 tubes coûtent 3000 €.
Toutenbois Merci! Bien que ce type de télescope dit "dobson" ne soit pas le plus approprié pour faire de l'astrophotographie, avec la motorisation, c'est cependant possible. Ceci dit, c'est quand même plus compliqué qu'avec un plus petit télescope.
Ces grands télescopes sont surtout consacrés à l'observation visuelle. C'est le plaisir de recevoir dans l'oeil des photons qui ont mis des millions d'années pour arriver jusqu'à nous. Personnellement, je ne pratique pas l'astrophotographie.
Plus le diamètre est grand, plus le nombre de photons récolté est grand, et donc, mieux on voit de détails.
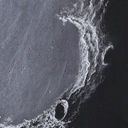
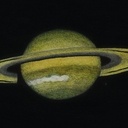
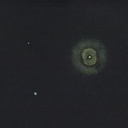
On peut voir de beaux détails sur les planètes, les volutes dans les bandes de Jupiter, les différences dans les anneaux de Saturne, de belles nébuleuses gazeuses, et plus le diamètre est grand, mieux on peut voir les couleurs. Et plein de galaxises, les spirales dans les plus grandes, et des amas de galaxies (plein de petites taches dans l'oculaire), qui sont à 300 millions d'années lumière...
Bien sur, cela n'a pas l'aspect des photos de Hubble ou du James Web...
Si je ne pratique pas l'astrophoto, je fais par contre des dessins, à partir des observations visuelles.
Ara Oui, cela fait longtemps que je me dis que je devrais me lancer dans le mobilier de jardin...
LeCongreDebout Merci! 
Toutenbois Viens quand tu veux, ce sera un grand plaisir de t'accueillir! A 50 km à l'ouest de Châlon sur saone.
Ara  Mais c'est une excellente idée!!
Mais c'est une excellente idée!!
GuiGuidesvolcans Merci!!!
Une oeuvre d'art! La Perfection. Prodigieux.
J'ai vu qu'elle sera exposée au Grand Palais au mois de mai ?
julien hardy ébéniste Cela donne envie d'aller à Paris pour les voir...
Pour ma part, si je devais dire toutes les fois que "je n'accède pas à l'esthétique de la pièce", on n'en finirait jamais... 
Ara Voyons, voyons, c'est pas une centrale nucléaire... 
Y a pas de règles. On fait ce qu'on veut en matière d'art... On peut tout mélanger, et on peut même peindre de l'ébène en blanc si on veut (ou de l'ivoire en noir).
Nicoel Le prix de ce genre de choses n'a rien de rationnel. C'est de l'artisanat d'art. Donc, c'est comme le marché de l'art. Cela peut atteindre des sommets. Cela dépend de plein de facteurs. L'originalité, le truc qu'on en encore jamais vu, la reconnaissance, l'implication internationale, le réseau, l'engouement, la hype, la chance. Il suffit qu'un type des Palisades en achete un, et ses copains vont faire pareil, et c'est parti... Le Monsieur a gagné plusieurs concours internationaux...
Nicoel Dans ce type de marché, il n'y a aucun échelle de valeurs et cela ne se vend pas au poids.
Cette table peut se vendre 500, 20 000 ou 30 000+ €. Comme déjà dit, ça dépend si ça entre dans la hype ou pas.
ebenober J'ai un client, un peintre allemand connu (c'est rare, un peintre qui fait de l'astronomie...). Il fait de la peinture abstraite, en très grand format (3m x 4m). Il m'a raconté que l'une de ses oeuvres a brûlé dans une maison à Malibu, dans un incendie il y a quelques années. Son client lui a demandé d'en refaire une à peu près semblable. Ses peintures se vendent entre 500 et 800 000 €...
Ara Je me fous de savoir l'heure. Ce qui m'intéresse, c'est de faire le truc.
Si je comprends bien, il s'agit d'une "boite" haute de 150 cm; 50 de large et 35 de profond, réalisée sous forme d'une structure avec cadres, et avec des panneaux intérieurs en cp de 15 ou 18 mm d ' épais intégrés dans les rainures du cadre ?
Donc, tout est contraint, et les panneau de cp, pas du massif, sont déjà d'une très forte épaisseur (18 mm!)
Perso, comme ça, au feeling, je ne m'embêterais pas... placage d'un seul coté. Je suis assez ceinture et bretelle, mais là, faut quand même pas exagérer...
Je sais bien que la règle, c'est la règle, c'est placage des deux cotés, et les "tradi" vont sortir les deux parachutes et te dire qu'il faut plaquer des deux cotés, mais ça, c'est pour du placage sur du massif, et pour des trucs non contraints. Dans ton cas, je ne vois pas trop comment cela pourrait bouger.
Ceci étant dit, cela ne coûte pas grand chose de plaquer des deux cotés... 






















Toujours aussi classe!