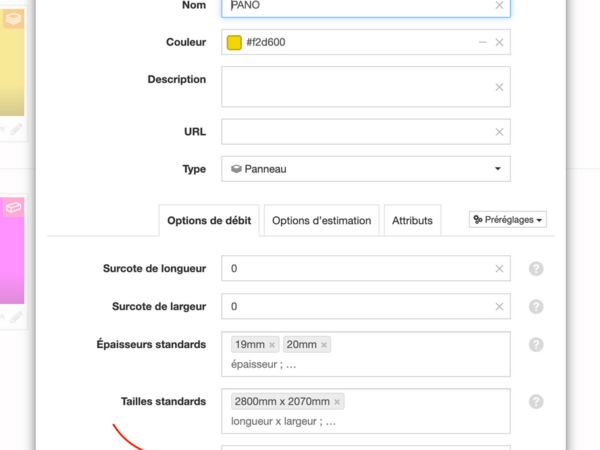
Je n’ai pas de tuto. La gestion de la quincaillerie dans OCL est sommaire. Il n’est possible que d’appliquer une matière a laquelle il faut configurer un type accessoire sur les composants pour les compter.
Quant au prix et la masse de la quincaillerie ça se défini dans les propriétés de la pièce et non celles de la matière.
Bonjour,
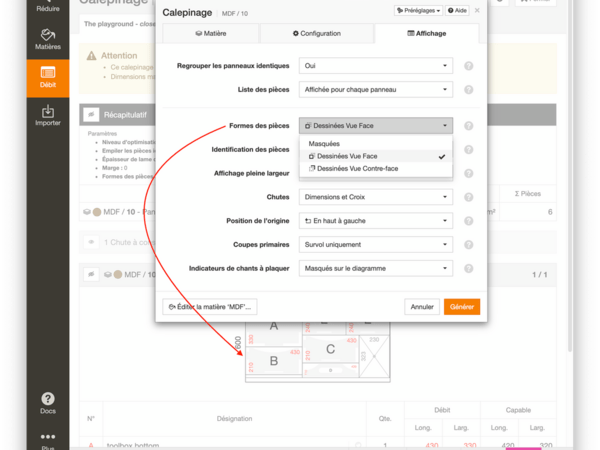
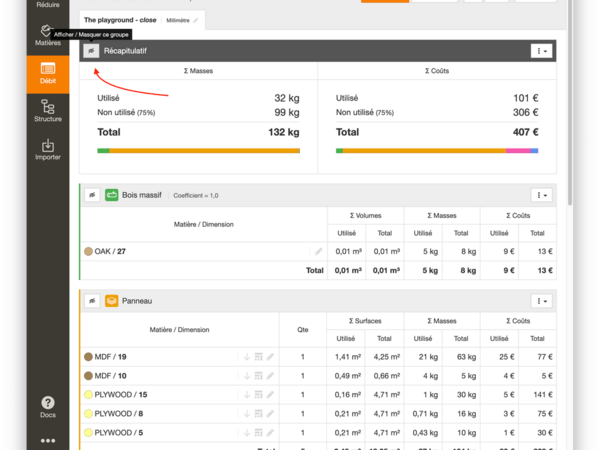
Pour ne pas afficher le récapitulatif de Masss et Coût, il suffit de le masquer en appuyant sur le bouton Masquer ce groupe du bloc "Récapitulatif".
Pour les colonnes dans les autres tableau, il n'y a pas d'option pour les masquer. Etant donné que c'est la donnée principale qui est calculée par le module Estimer.
Mais si tu ne mets pas de prix ou de masse volumique les colonnes seront vides.
Pour exporter en PDF, comme dans tout le reste du plugin, c'est possible en cliquant sur Imprimer et en choisissant l'Imprimante PDF dans la liste des imprimantes. C'est une fonctionnalité native à ton système d'exploitation qui marche avec tous les logiciels.
Et si le récapitulatif est masqué, il ne sera pas imprimé.
Non.
Par défaut la matière de la pièce est appliquée à l'instance du composant et si aucune face du dessin de la définition n'a encore de matière, alors tout prend la couleur de la matière de l'instance. C'est le fonctionnement de base de propagation des matières de SketchUp.
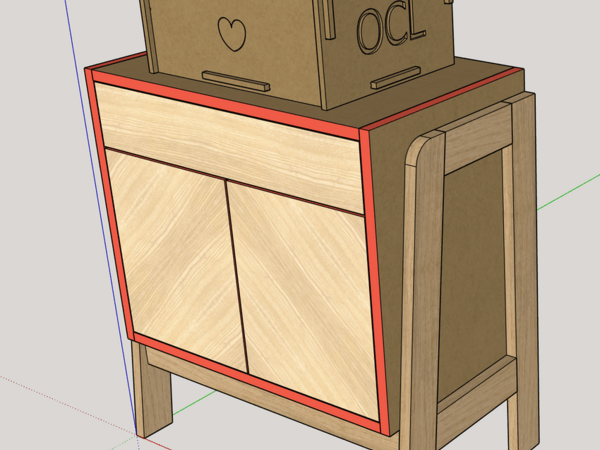
Il faut mieux prendre le problème à l'envers. Pour être en mesure de voir où il y a des chants, le mieux, c'est d'utiliser une une couleur flashy pour la matière chant.
Et au moment de faire un joli rendu au client, il suffit de remettre la couleur qui convient sur la matière chant. C'est 2 clics.
La bonne nouvelle est que c'est déjà possible.
Voici la manière la plus simple :
En premier lieu, il faut que la matière ait le paramètre Fil à Le fil suis la longueur.
Ensuite, tu peux utiliser l'outil Orienter les pièces avec l'action Permuter Longueur <-> Largeur pour faire tourner les axes du composant et donc le sens du fil en cliquant, dans le modèle 3D, sur les pièces que tu veux réorienter.
Pour rappel, si l'orientation de la pièce n'est pas automatique, la longueur est lue le long de l'axe rouge et la longueur est la direction du fil.
A noter aussi que dans le cas d'un fil travers, la longueur sera plus courte que la largeur.
Il me semble que TpaCAD accepte l'importation de fichier DXF.
Si c'est bien le cas, tu peux exporter toutes les pièces en DXF avec OpenCutList (en activant bien l'analyse de percements) et les importer dans TpaCAD qui devrait reconnaitre les cercles comme des percements, non ?
Sinon, je ne connais pas de plugins qui fasse des fichiers TCN directement.
Pour ce qui est d'exporter tous les détails d'une pièces en 2D avec du code Ruby, à par t'envoyer vers les sources d'OpenCutList qui combinent une petite centaine de lignes de code en ruby et bien plus dans une lib en C++ pour décomposer la projection 2D, j'ai pas mieux.
Oui, on peut parfaitement faire en sorte que le fil des textures suive le fil vu par OpenCutList.
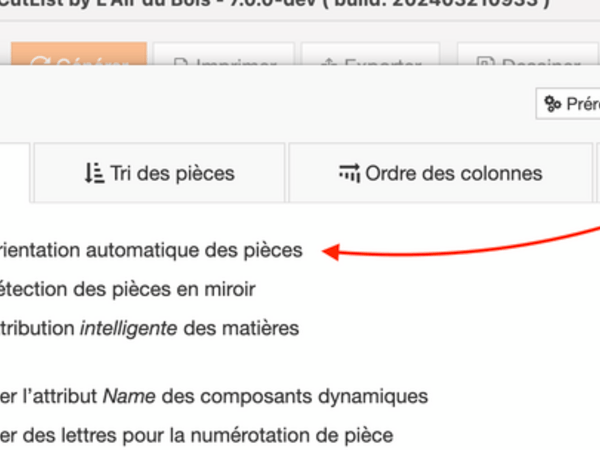
1 - Désactiver l'option "Orientation automatique des pièces".
votre citation iciCette option permet à OpenCutList de prendre la longueur sur la plus grande dimension sans se soucier des axes. La longueur étant aussi le sens du fil.
2 - Toujours appliquer les matières sur les instances et jamais sur les faces du dessin de la pièce.
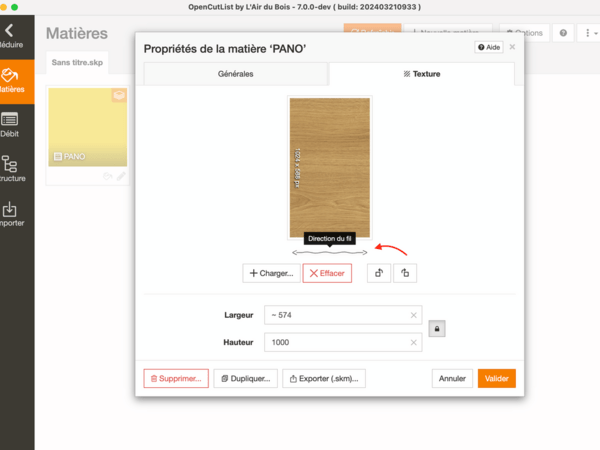
3 - Tourner l'image de la texture pour que le fil soit en l'horizontal (axe X)
4 - Utiliser l'outils "Adapter les axes" ou tout simplement l'outil "Axes" de SketchUp pour placer l'axe rouge dans la direction voulue du fil de la pièce.
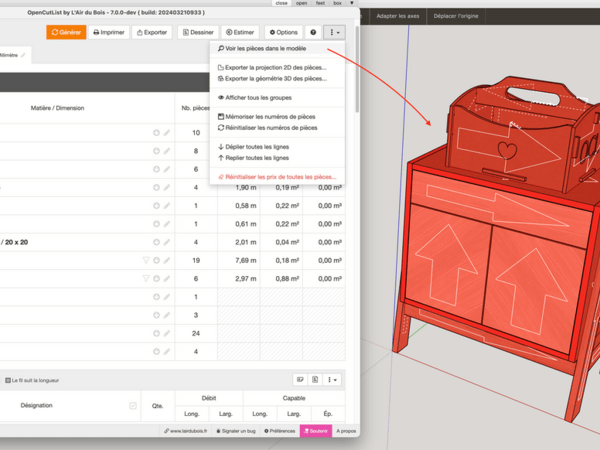
5 - Il est possible de vérifier le sens du fil vu par OpenCutList avec la fonction "Voir les pièces dans le modèle".
Ainsi dès que l'axe rouge change, les textures appliquées sur l'instance tournent avec lui. Voilou.
Une matière est une notion abstraite qui défini un objet applicable sur des éléments de dessin et qui peut contenir une couleur unie et/ou une texture.
Il n'y a pas de matières OCL, les seules matières qui existent sont celles créées dans le modèle courant SketchUp. Créer une matière via OCL n'est qu'un raccourcis à le faire avec les outils natifs de SketchUp.
Dans SketchUp, les matières du modèle peuvent être exportées et importées vers et depuis des fichiers externes (.skm). Là encore, OCL offre des raccourcis pour ça, mais c'est une fonctionnalité native de SketchUp.
Lien vers la documentation officielle : Ajouter des couleurs et des textures grâce aux matières